Вращение разрешает парадокс движения во времени и дает разгадку формулы Эйнштейна

СТО не отрицала движения во времени, а только не акцентировала внимание на нем, остерегаясь широкого обсуждения парадоксов четырехскорости, о которых мы говорили в разделе 1.2. Но и в теории движения во времени, развитой в [8], появляются парадоксы, не менее интересные, чем в СТО. В книге [9] описан, например, такой.
Если ускоренная элементарная частица - тардион в своем движении во времени отстает от окружающих ее неподвижных предметов лаборатории, то эта частица должна бы, по идее, вдруг бесследно исчезнуть из нашего поля зрения как бы в никуда, оставшись в нашем вчерашнем дне, в то время как мы вместе с лабораторией уже перешли в следующий момент времени. На практике же ускоренные частицы -тардионы не исчезают, а вместе с нами благополучно кочуют в будущее. Просто в них медленнее, чем у нас, протекают все внутренние процессы. Значит, движение во времени - это лишь внутренний процесс каждой частицы - тардиона? А вычерчивавшаяся нами и нашими предшественниками ось времени - это всего лишь математическая формальность, абстракция, не более того?
Но тогда четырехмерное пространство-время, с которым имеет дело теория относительности, - это всего лишь математический образ?! Неужели на самом деле существует только обычное трехмерное пространство?
Еще Птолемей писал на тему о размерности пространства и утверждал, что в природе не может существовать более трех пространственных измерений. И. Кант в XVIII веке, подчеркивая, что причина трехмерности нашего пространства еще неизвестна, отмечал, что только в трехмерном пространстве гравитационные силы могут быть обратно пропорциональны квадрату расстояний между телами. В XX веке П. Эренфест и Дж. Уитроу показали, что если бы число измерений пространства было больше трех, то существование планетарных систем было бы невозможным. Материальная точка в четырехмерном пространстве либо падала бы на силовой центр, либо уходила бы от него в бесконечность. Только в трехмерном мире могут существовать устойчивые орбиты планет в планетных системах [31 ].
Почему же тогда развитый в [8] формализм движения тел во времени как вдоль четвертой оси координат с учетом динамических характеристик этого мнимого движения так красиво и просто приводит к хорошо согласующимся с экспериментальными данными результатам, если четвертой оси координат не существует?
Ответ подсказывает теория электрона, разработанная В. М. Мигуновым из Запорожья [18]. Представьте себе движение электрического сигнала по цилиндрической спирали электроплитки. Он бежит по проволоке спирали со скоростью света. Это движение по цилиндрической спирали складывается из двух взаимно перпендикулярных компонент: движения вдоль оси спирали и движения по окружности витков проволоки. Скорости указанных компонент суммируются как векторы по теореме Пифагора, т.е. по формуле, аналогичной (1.16). Чем растянутее спираль, то есть чем больше ее шаг, тем больше скорость движения сигнала вдоль ее оси и тем меньше скорость и частота кругового движения. Если же спираль туго сжата с торцов в один виток-кольцо, то остается только круговое движение сигнала. Этот случай соответствует покоящейся в пространстве частице. Она неподвижна в пространстве, но сигнал (материя) в ней мчится по кругу со скоростью света.
Мигунов утверждает, что это и есть модель элементарной частицы. Только диаметр кольца в ней меньше классического радиуса электрона. А далее вспомним, что момент количества движения mCR материи в частице должен квантоваться, и запишем:

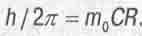(4.3)

Но 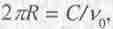, где v0 - частота вращения частицы, h - постоянная Планка.
Поэтому из (4.3) получается

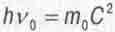(4.4)

В левой части здесь знаменитая формула Планка для энергии Кванта, в правой -не менее знаменитая формула Эйнштейна для энергии покоя Е0 тела. Мы получили то самое загадочное уравнение, о котором, как отмечалось в разделе 2.3, писал Л. Бриллюэн, что каждую из его частей невозможно вывести ни из одной существующей теории, что смысл этого равенства находится в глубокой тайне. Неужели тайны больше не существует?
Мигунов в [18] указывает, что соотношения (4.3) и (4.4) впервые получил еще в 20-е годы Луи де Бройль, который, как и мы сейчас, пытался найти связь между полной энергией частицы и частотой внутренних процессов в ней.
Если частица имеет конечный радиус R, то тангенциальная скорость движения материи в частице составляет величину

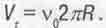(4.5)

Этой скорости соответствует величина 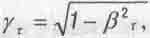где 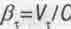. Отождествляя внутренне вращательное движение частицы с ее движением во времени, приравняем скорость последнего у С с тангенциальной скоростью Vт Тогда понятно, что с уменьшением у т при неизменном R частота v должна уменьшаться:

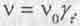(4.6)

Поэтому из (4.4) следует, что с повышением безразмерной тангенциальной скорости ß r движения материи в частице внутренняя энергия этой частицы должна не возрастать, как можно было предположить из формулы (2.3) СТО, а убывать:

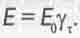(4.7)

Луи де Бройль в начале 20-х годов был настолько потрясен полученным результатом, противоречащим известной формуле теории относительности (3.1), что отказался от своей первоначальной затеи и реконструировал ее, приспосабливая к СТО.
Для этого он, исходя из выражения для полной (релятивистской) энергии частицы Е = Е0/ y и учитывая (4.4), записал:

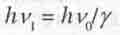(4.8)

и назвал величину

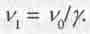(4.9)

частотой некой "фазовой волны материи", сопоставляемой с полной энергией частицы.
Так родилась теория де Бройля с ее непонятными "волнами материи" (позже названными "волнами де Бройля"). Их групповая скорость Vгр = dЕ/dРсоответствовала скорости V движения в пространстве частицы, имеющей импульс P=mV,a вот фазовая скорость Vф = E/P = С2(с в квадрате)/V принимала значения, большие скорости света С. Теоретики до сих пор заявляют, что фазовая скорость волны де Бройля относится к числу "принципиально ненаблюдаемых величин и имеет чисто символическое значение", (см. стр. 487 в [17]). Но думается, что теоретики опять поспешили с выводами, и на самом деле фазовая скорость волн де Бройля как-то связана с виртуальными частицами - тахионами, играющими немаловажную роль в процессах движения досветовых частиц - тардионов.
В теории де Бройля частота v1 уже не имела отношения ни к какому внутреннему процессу и возрастала с увеличением скорости V поступательного движения частицы, как возрастает частота фотона с ростом его энергии.
А отложенная де Бройлем в сторону первоначальная идея пролежала полвека, пока с нее не "стряхнул нафталин" украинский физик В.М. Мигунов.
Но обратите внимание на то, что полученная Луи де Бройлем формула (4.7) совпадает с формулой (3.6) для энергии движения тела во времени Ет. Не говорит ли это о том, что энергия движения элементарной частицы во времени Eт - это энергия внутреннего движения материи в частице?
Данная мысль смыкается с высказанным выше предположением о том, что мнимое движение во времени - это лишь внутренний процесс каждой элементарной частицы, к которому мы пришли из совершенно других предпосылок. Отождествление кругового движения материи в элементарных частицах с движением их во времени наводит на мысль и о том, что движение во времени элементарных частиц - тардионов не имеет внешней направленности. Траектория движения тардиона во времени должна быть не прямолинейной, а замкнутой внутри элементарной частицы. И когда мы чертим прямую ось времени, то как бы разматываем, распрямляем и натягиваем по прямой "нить времени", которая на самом деле как бы намотана на шпулю внутри элементарной частицы и вытягивается в цилиндрическую спираль при ее движении в пространстве. Не потому ли движение во времени мнимо, что это внутренне круговое движение в частице?
Последнее великолепно согласуется с теорией Калуцы - Клейна, предложенной еще в 20-е годы. В ней предполагается, что пространство-время имеет столько дополнительных измерений, сколько разного рода полей существует в природе. Но каждая дополнительная ось координат, начиная с пятой, как предположил 0. Клейн, "свернута" в петлю с диаметром ~10-32(10 в минус 32 степени) см (планковская единица длины). Поэтому движение вдоль такой оси координат ненаблюдаемо в макромире, но проявляется в виде разного рода полей. Электромагнитному полю, по Т. Калуце, соответствует пятое измерение.
В свете вышеизложенного нам остается только предположить, что ось времени тоже свернута в петлю с размерами порядка планковских. И что движение вдоль этой четвертой оси координат - оси времени - проявляется в виде гравитационного поля и сил инерции, что не противоречит теории Эйнштейна. Чем медленнее движение во времени, тем больше релятивистская масса и инерция тела, тем больше напряженность создаваемого им гравитационного поля.
Отождествление кругового движения материи в элементарной частице с движением ее во времени возвращает нас к старому спору о том, прямолинеен или цикличен ход времени. В античные времена наблюдения за распространенными тогда солнечными часами, стоявшими на центральной площади каждого города, привели философов к выводу, что "Время не подобно прямой линии, а описывает окружность" (Прокл, V в. н. э.). Эта точка зрения отражала единство противоположностей: ограниченность и вместе с тем бесконечность, обеспечиваемые свойствами окружности.
Объединение двух других противоположностей - замкнутости движения по окружности и безграничности прямолинейного движения - достигается в спирали, что подметил еще Архимед. Это объединение и используется в описанной выше спиралеобразной модели движения.
А.Д. Чернин в своей книге [32] указывает, что спиралеобразные узоры, символизирующие время, археологи находили на сосудах IY-III тысячелетий до н. э., а также на календаре, вырезанном на бивне мамонта, найденном в Сибири. Значит, мы не первые. И это радует, ибо древние люди знали кое-что такое, до чего мы еще не додумались. Наверно, они несли с собой отголоски каких-то очень глубоких знаний предыдущих цивилизаций.

4.4. Релятивистское обобщение теоремы вириала требует энерговыделения при ускорении вращения тел

Получив в начале 20-х годов так удивившую его формулу (4.7) для внутренней энергии вращающейся элементарной частицы, Луи де Бройль почему-то не обратил внимания на то, что она очень напоминает уже известную к тому времени формулу Планка-Лауэ (3.13) для релятивистского преобразования количества теплоты, и отказался от своей формулы. Теперь понятно, что совершенно напрасно отказался. Он, видимо, тоже со временем понял это. Потому-то в 60-е годы Луи де Бройль с таким энтузиазмом отстаивал формулы Планка и Лауэ [20].
Но некоторые толкователи теории относительности, например [33], и в наши дни вопреки (4.7) утверждают, что чем быстрее вращается тело, тем больше должна быть его полная масса-энергия, потому-де, что к энергии покоя этого тела добавляется кинетическая энергия вращения тела. Попробуем сосчитать так ли это.
Рассмотрим планету с массой m0, обращающуюся с тангенциальной скоростью Vт по круговой орбите с радиусом R вокруг Солнца или другой звезды, имеющей массу М. Центробежной силе

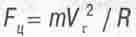(4.10)

в планетной системе противодействует сила гравитационного притяжения планеты к звезде

(4.11)

Отметим, что в эти формулы входит релятивистская масса m = m0/ y, где 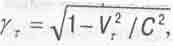учитывающая возрастание массы планеты при движении ее со скоростью Vr.
Орбита планеты равновесна, если указанные силы уравновешивают друг друга:

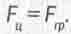(4.12)

Такое уравнение, включающее в себя сумму действующих на тело сил, в механике называют уравнением движения данного тела. Оно определяет движение тела в пространстве, а мы добавим: и во времени.
Подставим в (4.12) значения Fц и Frp из (4.10) и (4.11) и найдем из получившегося развернутого уравнения выражение для радиуса равновесной (устойчивой) орбиты.

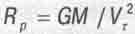(4.13)

Учитывая, что Vт = w R, где w = 2л(число пи)/T - угловая частота обращения планеты, олучим:

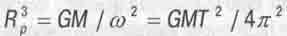(4.14)

Это греши закон Кеплера: квадраты периодов обращений планет Г соотносятся как кубы радиусов их орбит Я. Исходя из этого эмпирического закона, найденного И. Кеплером в начале XVII века по наблюдательным астрономическим данным, собранным Тихо Браге, И. Ньютон разработал свой знаменитый закон всемирного тяготения (4.11). Только ни Ньютону, ни Кеплеру не были известны величины G и M по отдельности, а из наблюдательных данных можно было вычислить лишь их произведение. Потому еще около ста лет закон всемирного тяготения являлся, по существу, лишь гипотезой до тех пор, пока в 1789 г. Г. Кавендиш не осуществил свой знаменитый эксперимент по определению величины гравитационной постоянной G, названный современниками "взвешиванием Земли и Солнца". Вот тогда-то гипотеза Ньютона превратилась в строгую теорию, которой астрономы пользуются и поныне.
На устойчивой круговой орбите планета обладает кинетической энергией движения по орбите:

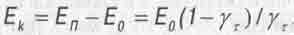(4.15)

где 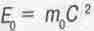- энергия покоя планеты, Еп = Е0/ у т - ее полная (релятивистская) энергия.
С другой стороны, планета в гравитационном поле удерживающей ее звезды обладает потенциальной гравитационной энергией

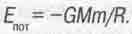(4.16)

Эта энергия считается отрицательной, поскольку это энергия связи, и возникает она от действия сил притяжения, а не отталкивания.
Ниже мы увидим, что эта энергия отрицательна отнюдь не условно, а потому, что она уходит из связанной силами тяготения системы.
Из формулы (4.13) понятно, что фигурирующая в (4.16) комбинация GM/R определяет квадрат тангенциальной скорости Vr движения планеты по равновесной круговой орбите. И тогда, подставив в (4.16) еще и значение m = m0/ y r, получим вместо (4.16) еще одно выражение для потенциальной энергии планеты в гравитационном поле звезды:

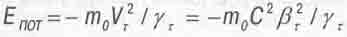(4.17)

Отношение потенциальной энергии тела, находящегося на устойчивой круговой орбите, к его кинетической энергии

(4.18)

последователи Эйнштейна назвали релятивистским обобщением теоремы вириала [14]. При малых скоростях движения Vr, когда у т~ 1, это выражение переходит в уравнение классической теоремы вириала

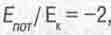(4.19)

открытой Р. Клаузиусом в 1870 г. Последняя гласит, что отрицательная потенциальная энергия связанной равновесной системы типа планетной по абсолютной величине в 2 раза больше суммарной кинетической энергии движения всех тел данной системы относительно ее центра масс. Только при таком условии планета удерживается на круговой орбите. При возрастании кинетической энергии свыше данной величины орбита планеты сначала превращается из круговой в эллиптическую, а когда |Ек| становится равной |Епот| - вообще перестает быть замкнутой, и планета (или космический корабль) уходит от звезды по параболической траектории. Потому-то вторая космическая скорость и называется параболической и потому - то она в 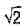раз больше первой. Подчеркнем: при первой соблюдается равенство противодействующих сил, при второй - энергий, связанных с ними.
А теперь вычислим суммарную энергию планеты. Она состоит из суммы энергий покоя Е0, кинетической Ек и потенциальной Епот и составляет

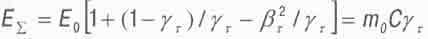(4.20)

Это выражение верно только когда масса планеты т0 много меньше массы удерживающей ее звезды, что и реализуется в Солнечной системе.
Для нас будет интересен еще случай, когда масса притягивающего центра M равна массе "планеты" m0. Такой случай реализуется, например, в двойных звездах, обращающихся вокруг их общего центра масс. При этом суммарная масса-энергия системы составляет:

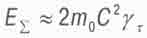(4.21)

Разница между суммарной массой-энергией связанной системы ЕЕ и суммой масс-энергий покоя составляющих ее объектов называют дефектом массы, или энергией связи системы:

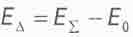(4.22)

Для первого случая (планеты в Солнечной системе) она составляет величину

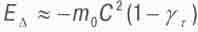(4.23)

Для второго случая (двойной звезды) энергия связи в 2 раза больше. Как известно, силы притяжения F между положительным и отрицательным электрическими зарядами е протона и электрона описываются законом Кулона, отражающим такую же квадратичную зависимость от расстояния R между этими частицами, как и закон всемирного тяготения:

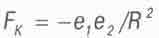(4.24)

Поэтому вышенайденные формулы пригодны и для описания движения электрона в резерфордско-боровской модели атома и в позитронии - связанной системе из электрона и позитрона (антиэлектрона, имеющего положительный электрический заряд), вращающихся вокруг общего центра масс. Позитроний уже в середине XX века синтезировали в лабораториях, но до сих пор еще не осознали до конца, какую важную роль он играет в физике вакуума.
Когда же мы рассматриваем не планетную систему или электроны в атоме, а, например, вращающийся диск, то вместо сил гравитации или кулоновских сил притяжения должны учитывать возникающие силы упругости материала диска, описываемые законом Гука, которые препятствуют разрыву диска центробежными силами. Это усложняет задачу, но мы здесь не будем приводить ее решение, а учтем лишь, что силы упругости в конечном счете сводятся к электромагнитным силам взаимодействий между атомами, из которых состоят тела. Поэтому последняя задача сводится ко второй.
Из выражений (4.20) и (4.21) понятно, что с ростом тангенциальной скорости Vr движения по орбите суммарная масса-энергия системы уменьшается. Рекомендуем удивиться этому результату. Ведь до сих пор мы полагали, что с ростом скорости движения тел их массы-энергии возрастают согласно релятивистской формуле 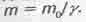. А тут, при вращательном движении, имеем:

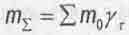(4.25)

Это означает, что суммарная масса-энергия системы связанных тел с увеличением скорости ее вращения уменьшается!
Осознать возможность подобного даже такой ум, как Луи де Бройль, в свое время не решился.
Можно показать, что данная закономерность относится не только к планетным системам и атомам, но и вообще к любым вращающимся телам, в том числе и к колесу Вашего автомобиля, ибо во всякой вращающейся системе обязательно должны присутствовать центростремительные силы, противодействующие центробежным и равные им. Их наличие и обуславливает появление отрицательной энергии связи и соответствующего ей дефекта масс. Об этом обстоятельстве авторы учебников и книг по СТО почему-то не упоминают. А вот экспериментаторы-"неформалы" давно подметили "странное" поведение гироскопов на весах: быстро вращающийся гироскоп весит чуточку меньше, чем неподвижный. Одни утверждают, что если еще сильнее раскрутить, то гироскоп взлетит под действием "антигравитации", другие называют их фальсификаторами. Оно и неудивительно, ибо даже некоторые маститые толкователи теории относительности почему - то не знают формулы (4.25).
А ведь эту формулу мы уже встречали в теории движения во времени [8]. Да и здесь мы уже имели выражение (3.6) для энергии движения тела во времени 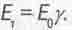. Оно почти идентично выражениям (4.20) и (4.25) и показывало, что энергия движения тела во времени уменьшается линейно с уменьшением скорости его движения во времени у. Только там мы имели дело не с вращательным, а с поступательным движением тела в пространстве. При этом энергия движения тела во времени Eт там не была равна суммарной энергии тела, а составляла лишь часть полной энергии тела Еп.
Второй частью является энергия движения в пространстве (или энергия переноса), которая определяется формулой (3.5). Эта формула неслучайно так похожа на формулу (4.17), определяющую отрицательную потенциальную энергию притяжения друг к другу тел связанной вращающейся системы. Ведь если в такой системе при вращении остается только энергия движения ее во времени Ет, а энергия переноса должна уйти из системы, то эта энергия переноса Ev должна быть эквивалентна дефекту массы-энергии системы, то есть равна ее энергии связи. Получается, что при вращении тела оно не обладает энергией переноса Ev, ибо нет самого переноса центра масс тела.
В разделе 3.2 мы отмечали, что при поступательном движении тела невозможно отделить Ет от Ev. Наблюдатель имеет дело только с Еп. И еще гадали как бы ухитриться выделить Еv из Еп с тем, чтобы использовать Ev в виде излучений и иметь выигрыш в энергии 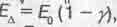, который пустить на производство электроэнергии. Теперь мы мдим, что Е∆ - это и есть энергия связи (или дефект массы-энергии), которая сама стремится выделиться в составе Ev из системы при ее вращении. А у вращающейся истемы тел остается только энергия движения во времени 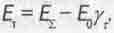. Энергия же Ev должна покинуть систему при ускорении ее вращения. Иначе система окажется в неравновесном состоянии и может развалиться.
Посмотрим как величина Еv связана с кинетической энергией вращения системы 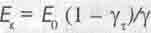. Согласно ее определению величина

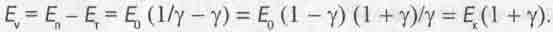(4.26)

При малых по сравнению со скоростью света тангенциальных скоростях Vr вращательного движения у r~ 1. Поэтому при технических скоростях вращения тел

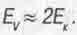(4.26)

И если энергия Ev уходит из системы в виде излучений, то это означает, что на каждый вложенный во вращение Джоуль кинетической энергии должно выделиться 2 Джоуля лучевой энергии.
То, о чем мы только мечтали, реализуется при вращении тел! Безусловно, это открывает огромные перспективы перед энергетикой, обещает доселе невиданные источники даровой энергии. Похоже, что по своей эффективности они смогут превзойти возможности атомной энергетики. И, наконец, они обещают быть экологически чистыми источниками.

Date: 2015-07-27; view: 1046; Нарушение авторских прав