Построение графиков простых гармонических колебаний

Предположим, что точка-М движется рав­номерно, с постоянной угловой скоростью (рад/сек) против часовой стрелки по окружности радиуса O1M центром в точке O1. Пусть в начальный момент времени, т. е. при

t = 0, движущаяся точка находилась в точке М12, положение которой определяется углом 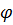. Тогда через tсек точка перейдет в положение М, определяе­мое углом 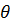= 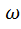t+ .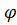

Рассмотрим, как перемещается проекция точки М на вертикальный диаметр O1К при равномерном враще­нии точки М. Из O1MKочевидно, что O1K(= O1Msin или у=A sin(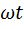 + 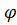). Это уравнение и определяет за­кон, по которому совершает колебательное движение проекция К точки М на вертикальный диаметр. Такого рода движение точки К называется простым гармониче­ским колебанием.

Из выражения у=A sin(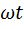 + 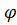)ясно (если учесть ктому же, что

cos 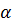=sin (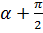), что рассмотренныев пункте 4 примеры относятся к простым гармоническим колебаниям).

Построение графика функции у=A sin(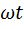 + 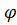) произведено следующим образом: ок­ружность, по которой движется точка М, разделена на 12 равных частей; на оси Ot отложен произвольный от­резок ОТ, соответствующий полному циклу колебаний точки K. Этот отрезок разделен на 12 равных частей. Че­рез точки деления проведены прямые, перпендику­лярные оси Ох, и на них отложены отрезки, равные ординатам соответствующих точек окружности. Соеди­няя полученные точки плавной кривой, получаем одну «волну» (один период) функции у=A sin( 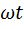+ 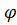). Такой способ построения данного графика дает возможность уяснить геометрический смысл параметров простого гар­монического колебания: А, и .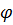

Величина А —радиус круга — является наибольшим отклонением точки К от центрального положения O₁и называется амплитудой колебания.

Переменный угол 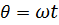+ 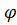, определяющий' текущее положение точки М, называют фазой, Я угол 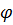, опре­деляющий начальное положение точки M12, — начальной фазой.

Время T, в течение которого точка М совершит полный оборот, а точка К — полный цикл колебания, назы­вают периодом гармонического колебания. Очевидно, Т — период функции у=A sin(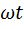 + 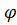), — угловая ско­рость вращения точки М (ее называют угловой часто­той).

Известно, что Т =2 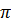, откуда

, .

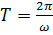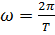Величина, обратная периоду колебания, т. е. ,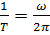

называется частотой (она показывает, сколькоколебаний в секунду совершает точка К).

Что же надо знать для построения графика функции

у=A sin(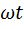 + 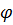)= A sin (t+ )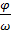

непосредственно? Надо знать величину амплитуды А (чтобы определить «высоту» графика); величину , покоторой находится Т = 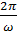дляпостроения удобнееискать сразу четверть периода 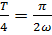; чтобы определить, насколько сдвинута заданная синусоида относи­тельно графика y=А sin 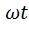, нужно знать величину

;

Точка на оси t с координатой 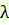со­ответствует (y=А sin ( 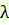+ положе­

нию точки М в правом конце горизонтального диамет­ра. Отсюда и метод построе­ния: из формулы колебания определяем А и проводим две прямые y =|A| (между ними будет заключен весьграфик); определяем 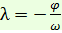и отмечаем на оси абсцисс точку t= 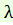(с этой точки начинается положитель­ный полупериод синусоиды); определяем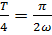

и откладываем от точки t= 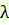на оси абсцисс четыре та­ких отрезка, после чего построение графика очевидно.

Список литературы:

Егерев В.К., Радунский Б.А., Тальский Д.А.

«Методика построения графиков функций.»

Date: 2015-07-27; view: 358; Нарушение авторских прав