Главная Случайная страница


Полезное:

Как сделать разговор полезным и приятным Как сделать объемную звезду своими руками Как сделать то, что делать не хочется? Как сделать погремушку Как сделать так чтобы женщины сами знакомились с вами Как сделать идею коммерческой Как сделать хорошую растяжку ног? Как сделать наш разум здоровым? Как сделать, чтобы люди обманывали меньше Вопрос 4. Как сделать так, чтобы вас уважали и ценили? Как сделать лучше себе и другим людям Как сделать свидание интересным?


Категории:

АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника






Сдвига с деформациями

⇐ ПредыдущаяСтр 3 из 4Следующая ⇒

 

1.Построение графика функции y=Af(x)

Правило 7. Для того чтобы построить график функ­ции y=Af(x),надо ординаты всех точек графика функ­ции y=f(x)увеличить по абсолютной величине в А раз,если А>1, и уменьшить в раз, если 0<A<1 (инымисловами, надо изменить ординаты всех точек графика функции y=f(x)в отношении 1: А).

В самом деле, пусть график функции y=f(x) изве­стен и А> 1. В произвольной точке х0 отрезок СВ = f(x0), a DB=Af(x 0), откуда 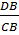=A(или СВ: DB=1:A), т. е. ордината точки графика функции y = Af(x) в точке x 0 в А раз больше соответствующей ординаты графика y = f(x). Отсюда, в силу произвольности выбора точки х0 (из области определения функции y = f(x)), и следует справедливость правила 7 для рассмат­риваемого случая. Ана­логично убеждаемся в справедливости прави­ла 7 при 0<A<1.

На основании пра­вила 7 можно устано­вить, что переход от графика функции у= f(x) к графику функ­ции y=Af(x) осуществляется с деформацией, а именно, при A>1 - график функции у=f(x) «растягивается», а при 0<A<1 «сжимается» вдоль оси ординат. При этом ну­ли функции, естественно, остаются на своих местах (все нули функции y=f(x) являются нулями функции у = Af(x) и наоборот).

Замечание. При отрицательном А для построения графика функции y=Af(x) следует использовать два

правила: правило 7 — для построения функции 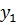= |A|f(x), а затем правило 4 — для построения графикаy= -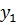

 

2.Построение графика функции y=f( 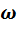x)

Правило 8. Для того чтобы построить график функ­ции y=f( 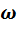x) ( > 0), надо абсциссы всех точек графика функции y=f(x)уменьшить по абсолютной величине в

раз, если >1, и увеличить в раз, если 0< <1

(иными словами, надо изменить абсциссы всех точек графика функции y=f(x)в отношении : 1).

В самом деле, пусть график функции y=f(x) изве­стен и >1.

Возьмем произвольное значение аргумента х0 (из об­ласти определения функции y=f(x)). Тогда отрезок AB=f(x0). Но функция y=f( х) принимает то же самоезначение в точке D с абсциссой 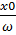, так как y=f( x) =f(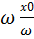)=f(x0).

Таким образом, функция y=f( x) проходит все зна­чения функции y=f(x) (в силу произвольности выбора x0) в точках, абсциссы которых по абсолютной величине в раз меньше соответствующих абсцисс функции y=f(x)

В справедливости пра­вила 8 при 0< 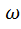<1 мож­но убедиться аналогично. Таким образом, переход от графика функции у=f(x) к графику y=f( x) осуществляется дефор­мацией графика, y=f(x) вдоль оси абсцисс (при >1 график функции «сжимается» в раз, а

при 0< 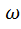<1 — «растягивается» в раз). При этом точки пересечения графика с осью ординат остаются на ме­сте (так как при х=0 х = 0).

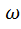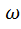Замечание. При отрицательном ( <0) для по­строения графика функции y=f( х) следует использо­вать два правила: правило 8 — для построения графика функции y = f( | |х), а затем правило 5 — для построе­ния графика y = f( х) =/(-| |х).


 

3.Построение графика функции y=Af( 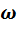х)

Правило 9. Для того чтобы построить график функции y=Af( x),где A>0 и >0, надо ординаты всех точек графика функции y=f(x) изменить вотношении 1: А, а абсциссы всех точек полученного графика изме­нить в отношении : 1. В этой формулировке, для сокра­щения, не рассматриваются случаи: А> 1; А< 1; >1; < 1. Все эти случаи объединены словами: «изменить в отношении 1 :А» и «изменить в отношении : 1».

 

4.Построение графика функции y=Af( 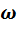x+n) + m

Правило 10. Для того чтобы построить график функ­ции y=Af( x+n) + m =Af [(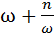)]+m, надо:

1) Ординаты всех точек графика функции y=f(x) изменить в отношении 1: А. При этом производится де­формация в направлении оси. ординат (а при A<0 и отражение относительно оси абсцисс).

2) Абсциссы всех точек полученного графика изме­нить в отношении :1. При этом производится деформа­ция в направлении оси абсцисс (а при A<0 и отраже­ние относительно оси ординат).

3) Сдвинуть полученный график вдоль оси абсциссна - .

4) Сдвинуть полученный график вдоль оси ординат на т.

Данное правило раскрывает «динамику» построения графика заданной функции. Кроме того, это правило объединяет все предыдущие (кроме правила 6),"и если принять его за основу, то правила 1, 2, 3, 4, 5, 7, 8 и 9 получаются из него как частные случаи при тех или иных значениях параметров: A, , т и п.

Например, правило 3 является следствием правила 10 при А = =1 и произвольных т и п; правило 5 — при A = 1, т = п= 0, = -1; правило 8 — при A = 1, т = п = 0 и произвольном и т. д.


 


 

⇐ Предыдущая1234Следующая ⇒





Date: 2015-07-27; view: 288; Нарушение авторских прав


mydocx.ru - 2015-2025 year. (0.008 sec.) Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав - Пожаловаться на публикацию