Движений без деформаций

Построение графиков функций путем

движений без деформаций

Часто бывает, что график функции у = f(x) заведомо известен (например, если f(x) —одна из основных эле­ментарных функций или если он был уже построен при решении одной из предыдущих задач), а требуется пост­роить график функции, тесно связанной с данной.

В ряде случаев это может быть сделано довольно просто.

1. Построение графика функции y=f(x)+ а

Правило 1. Для того чтобы построить график функ­ции у =f(x) + а, надо кривую у =f(x)сдвинуть вдоль оси ординат на а единиц (с учетом знака а) без дефор­мации (как одно целое).

В самом деле, если а > 0 и нам известен график функции y =f(x), то для произвольной точки х₀ (из области определения функции) отрезок

AC = f( ),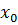

а отрезок

ВС = f( 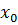) + a.

Отсюда очевидно, что разность этих ординат ВС — АС = а, т. е. ВС = АС + а, и для получения точки графика функции у = f(x) + а при х = х₀ надо к орди­нате функции в этой точке y=f(x ₀) прибавить величи­нуа. Точка х₀ была выбрана произвольно, а потому наше рассуждение справедливо для всех точек в области опре­деления функции у = f(x). При а<0 ординаты кривой y = f(x)+a будут меньше соответствующих ординат кривой y=f(x) на величину а, т. е. сдвиг надо будет про­извести в отрицательном направлении вдоль оси орди­нат (вниз).

2. Построение графика функции y = f(x+a)

Правило 2. Для того чтобы построить график функ­ции y = f(x+a),надо кривую у = f(x)сдвинуть без де­формаций вдоль оси абсцисс на а единиц (с учетом знака а).

Пусть a >0 и известен график функции y =f(x). Рассмотрим значение функции y= f(x + a) в произвольной точке :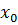

y= f(x₀ + а) = АВ.

Но такая же ордината будет и у кривой у = f(x) в точ­ке х = Хо + а:

А'В' = f(x₀ + а) = АВ.

При сравнении кривых видно, что в силу произволь­ности х₀ функция у = f(x + а) проходит такие же значе­ния, что и функция y=f(x) только на а единиц левее. Следовательно, график функции у= f(x+ а) можно по­лучить путем сдвига кривой y=f(x) вдоль оси Ох на величину а в отрицательном направ­лении (а>0). Если а<0, то кривую y=f(x+a) можно построить аналогично путем сдви­га графика y=f(x) в положительном направ­лении.

3. Построение графика функции у = f(x + n) + т

Правило 3. Для того чтобы построить график функ­ции y = f(x + n)+m_tнадо кривую y = f(x)сдвинуть вдоль оси абсцисс на «- п» единиц, и вдоль оси ординат на «т» единиц (с учетом знаков тип).

4. Построение графика функции у=-f(x)

Правило 4. Для того чтобы построить график функ­ции у = -f (x), надо построить изображение, симметрич­ное графику функции у = f(x)относительно оси абсцисс.

Пусть график функции y = f(x) известен. Возьмем произвольную точку х₀ из области определения функции y=f(x). Значение функции у= — f(x) в этойточке будет - f(x ₀), а значение функции y = f(x) —со­ответственно f(x ₀). Они отличаются друг от друга толь­ко знаком. Откуда и очевидна симметричность точек M1и М относительно оси абсцисс, а в силу произвольности выбора х₀ — и справедливость правила 4.

5. Построение графика функции у = f( — х)

Правило 5. Для того чтобы построить график функ­ции у =f (-х), надо построить изображение, симметрич­ное графику функции у = f (х) относительно оси ординат.

В самом деле, пусть вид графика y = f(x) известен. В произвольной точке х₀ отрезок АВ равен (и по величине, и по знаку) значению функции у = f (х₀). Функция же y = f{ —х) принимает такое же значение при х = - х₀, т. е. в точке, симметричной относительно оси ординат А1B1 = АВ. Точки В и В₁ симметричны от­носительно оси ординат. А тогда из произвольности вы­бора точки х₀ следует справедливость правила 5.

Date: 2015-07-27; view: 332; Нарушение авторских прав