
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Задачи, решаемые на практическом занятии
|
|
Рассмотрим несколько примеров использования круговой номограммы.
Задача ПР1.1.
Пересчитать комплексное нормированное сопротивление 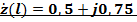 из сечения
из сечения 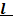 в сечение
в сечение 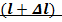 в сторону генератора. (
в сторону генератора. ( 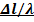 =0,065).
=0,065).
Процедура пересчета включает следующие шаги:
Шаг 1. Находим на круговой номограмме сопротивлений точку, соответствующую сопротивлению в сечении 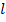 . Она лежит на пересечении окружности постоянного активного сопротивления, равного Re
. Она лежит на пересечении окружности постоянного активного сопротивления, равного Re 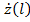 и линии постоянного реактивного сопротивления, равного Im
и линии постоянного реактивного сопротивления, равного Im 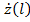 (т.1 на рис.1.3)
(т.1 на рис.1.3)
Определяем круг КБВ которому соответствует значение 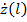 (КБВ=0,3). Переходим из т.1 по линии постоянного КБВ на расстояние
(КБВ=0,3). Переходим из т.1 по линии постоянного КБВ на расстояние 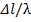 =0,065 в сторону генератора. Для этого проводим через точку 1 радиус вектор (прямая, проходящая через центр номограммы и заданную точку)
=0,065 в сторону генератора. Для этого проводим через точку 1 радиус вектор (прямая, проходящая через центр номограммы и заданную точку)  Пересечение этого радиус-вектора с окружностью, на которой нанесена шкала расстояний, дает нам возможность зафиксировать условное положение сечения
Пересечение этого радиус-вектора с окружностью, на которой нанесена шкала расстояний, дает нам возможность зафиксировать условное положение сечения 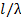 на этой шкале (т.2
на этой шкале (т.2 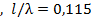 ).
).
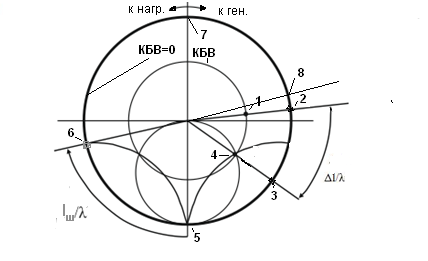
Рис. 1.3 Использование круговой номограммы для пересчета сопротивлений и проводимостей
Шаг 2. Отсчитываем от точки 2 по шкале расстояний величину 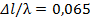 в требуемом направлении (по поставленному в рассматриваемой задаче условию в сторону к генератору). Отмечаем на шкале расстояний полученную точку (т.3,
в требуемом направлении (по поставленному в рассматриваемой задаче условию в сторону к генератору). Отмечаем на шкале расстояний полученную точку (т.3, 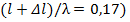 и проводим через нее радиус вектор.
и проводим через нее радиус вектор.
Шаг 3. Находим пересечение радиус вектора и круга КБВ=0,3. Значение сопротивления в точке пересечения (т.4) и есть искомое значение сопротивления в сечении 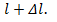
ОТВЕТ: 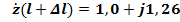
Задача ПР1.2.
Одной из задач, часто возникающих при проведении измерений и расчетов, является задача нахождения комплексного значения проводимости по известной величине сопротивления 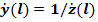 и наоборот. Данное преобразование может быть легко проведено с помощью круговой номограммы.
и наоборот. Данное преобразование может быть легко проведено с помощью круговой номограммы.
Пусть в некотором сечении линии нам известно значение нормированного сопротивления 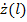 . Используя формулы для пересчета сопротивлений (проводимостей) из одного сечения линии в другое легко получить что:
. Используя формулы для пересчета сопротивлений (проводимостей) из одного сечения линии в другое легко получить что:
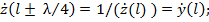
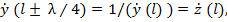
т.е. при пересчете нормированного сопротивления из сечения 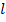 в сечение, отстоящее от него на расстояние 0,25λ в сторону генератора или нагрузки, мы получаем значение сопротивления, численно равное значению проводимости в исходном сечении
в сечение, отстоящее от него на расстояние 0,25λ в сторону генератора или нагрузки, мы получаем значение сопротивления, численно равное значению проводимости в исходном сечении 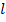 .
.
На круговой номограмме сопротивлений (рис. 4) описанная процедура пересчета сводится к нахождению сопротивления в точке т. 2, расположенной на номограмме сопротивлений диаметрально противоположно исходной точке (т.1), в которой сопротивление известно.
Аналогично с использованием номограммы проводимости находится сопротивление в заданном сечении линии по известной проводимости.
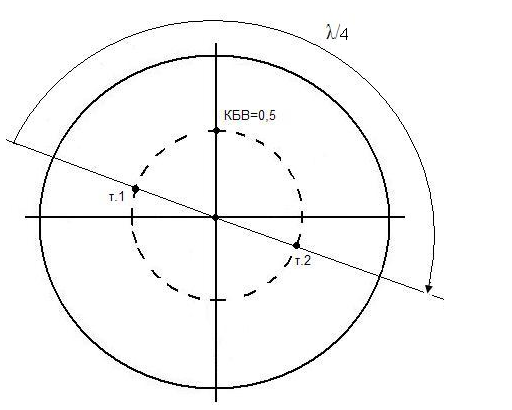
Рис. 1.4 Определение проводимости по известному сопротивлению с помощью круговой номограммы
Задача ПР1.3.
Определить нормированное сопротивление и проводимость на входе шлейфа с холостым ходом в сечении нагрузки при его длине 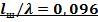 .
.
Шаг 1. Находим в рассматриваемом отрезке линии (шлейфе) сечение, в котором сопротивление известно. Для нашего случая - это сечение нагрузки, сопротивление которой равно бесконечности (режим хх на конце шлейфа). На номограмме сопротивлений рис. 3 сопротивление равно бесконечности в т.5, принадлежащей кругу КБВ=0.
Проводим радиус вектор через точку 5. Пересечение этого радиус-вектора с окружностью, на которой нанесена шкала расстояний, дает условное положение сечения 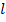 /λ на этой шкале (0.25).
/λ на этой шкале (0.25).
Шаг 2. Отсчитываем от найденной точки на шкале расстояний величину 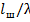 в направлении к генератору. Отмечаем на шкале расстояний полученную точку (т.6) и проводим через нее радиус вектор.
в направлении к генератору. Отмечаем на шкале расстояний полученную точку (т.6) и проводим через нее радиус вектор.
Шаг 3. Находим пересечение радиус вектора и круга КБВ=0. Значение сопротивления в точке пересечения zш=-j1,43 и есть искомое значение реактивного сопротивления на входе шлейфа (активная составляющая сопротивления на круге КБВ=0 равна нулю, поскольку этот круг одновременно является кругом, на котором Rez=0).
ОТВЕТ: zш=-j1,43
Проводимость может быть найдена путем пересчета сопротивления в проводимость по методике, изложенной в предыдущем примере (yш = j0,69).
Задача ПР1.4.
Определить длину шлейфа  с холостым ходом в сечении нагрузки, имеющего на входе заданную нормированную проводимость yш = j0,65.
с холостым ходом в сечении нагрузки, имеющего на входе заданную нормированную проводимость yш = j0,65.
Будем считать, что изображенная на рис. 3 номограмма есть номограмма проводимостей (выше отмечалось, что номограммы сопротивлений и проводимостей внешне не отличаются).
Шаг 1. В сечении нагрузки на конце шлейфа, проводимость равна нулю (режим хх). На номограмме проводимостей на рис. 3 проводимость равная 0 соответствует точке 7, принадлежащей кругу КБВ=0.
Проводим радиус вектор через точку 7. Пересечение этого радиус-вектора с окружностью, на которой нанесена шкала расстояний, дает условное положение сечения 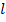 /λ на этой шкале (0).
/λ на этой шкале (0).
Шаг 2. Двигаясь от точки 7 по кругу КБВ=0 в сторону генератора, доходим до т.8, в которой проводимость равна заданной. Проводим через т.8 радиус-вектор и отмечаем на шкале расстояний соответствующее т.8 значение.
Расстояние от точки 7 до точки 8 и есть искомая длина шлейфа.
ОТВЕТ: 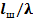 =0,095.
=0,095.
Задача ПР1.5.
Определить нормированную проводимость на входе шлейфа длиной 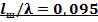 с коротким замыканием в сечении нагрузки.
с коротким замыканием в сечении нагрузки.
Шаг 1. Сечение, в котором проводимость известна является сечением нагрузки, проводимость которой в данном случае равна бесконечности (режим кз на конце шлейфа). На номограмме рис. 3 (номограмму на рис 3 мы рассматриваем как номограмму проводимостей) проводимость равна бесконечности в т.5, принадлежащей кругу КБВ=0.
Проводим радиус вектор через точку 5. Пересечение этого радиус-вектора с окружностью, на которой нанесена шкала расстояний, дает условное положение сечения 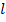 /λ на этой шкале (0.25).
/λ на этой шкале (0.25).
Шаг 2. Отсчитываем от найденной точки на шкале расстояний величину 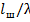 = 0,096 в направлении к генератору. Отмечаем на шкале расстояний полученную точку (т.6) и проводим через нее радиус вектор.
= 0,096 в направлении к генератору. Отмечаем на шкале расстояний полученную точку (т.6) и проводим через нее радиус вектор.
Шаг 3. Находим пересечение построенного радиус вектора и круга КБВ=0. Значение проводимости в точке пересечения yш=-j1,43 и есть искомое значение реактивной проводимости на входе короткозамкнутого шлейфа (активная составляющая проводимости на круге КБВ=0 равна нулю).
ОТВЕТ: yш=-j1,43
Задание на дом
1. С помощью круговой номограммы пересчитать сопротивление z = 0,5 - j 1,5 в проводимость.
2. Для сопротивления нагрузки, равного z н=2,5+ j 1,0, построить распределение нормированных напряжения и тока вдоль линии питания при движении от нагрузки в сторону к генератору в пределах одной длины волны.
3. Линия передачи с волновым сопротивлением z в=75 Ом нагружена на сопротивление z н =30+ j 45 Ом. Определить модуль коэффициента отражения от нагрузки. Какой КСВ установится в линии?
4. В линии передачи установился режим стоячей волны с КСВ=1,5. Чему равен модуль коэффициента отражения?
5. Нарисуйте графики изменения активной и реактивной составляющих эквивалентного сопротивления в сечении линии передачи при движении от нагрузки zн=0,6+j0,3 в сторону генератора в пределах одной длины волны.
Date: 2015-07-27; view: 782; Нарушение авторских прав