
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Нормированные напряжения и токи
|
|
Электродинамическое описание электромагнитного поля в линии передачи с помощью векторных функций Е и Н содержит в себе существенно больше информации, чем может потребоваться при расчете и проектировании трактов СВЧ. Поэтому подробности структуры полей, распределения и направления векторов поля, величина волнового сопротивления, измеренная в омах, после того, как выбран конкретный тип линии передачи, имеют второстепенное значение и при проектировании тракта эти факторы желательно исключить.
Достигается это построением универсальной математической модели в виде эквивалентной длинной линии. В эквивалентной длинной линии векторные функции распределения полей в поперечных сечениях заменяются интегральными (усредненными) мерами электромагнитного поля - эквивалентными нормированными напряжениями и токами для падающей и отраженной волн.
Нормированные напряжения и токи падающей и отраженной волн в некотором сечении 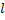 линии передачи вводятся с помощью соотношений:
линии передачи вводятся с помощью соотношений:
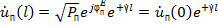 , (1.1)
, (1.1)
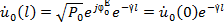 , (1.2)
, (1.2)
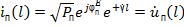 , (1.1’)
, (1.1’)
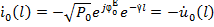 , (1.2’)
, (1.2’)
где координата 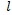 , направленная вдоль линии, отсчитывается от некоторого произвольного сечения линии, в котором
, направленная вдоль линии, отсчитывается от некоторого произвольного сечения линии, в котором 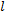 полагается равным 0. В направлении генератора величина
полагается равным 0. В направлении генератора величина 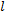 положительна, в направлении нагрузки – отрицательна. Чаще всего сечение
положительна, в направлении нагрузки – отрицательна. Чаще всего сечение 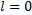 совмещается с сечением входа нагрузки.
совмещается с сечением входа нагрузки.
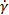 =α+jβ - коэффициент распространения для моделируемого типа волны, α- коэффициент затухания (Нп/м), β - коэффициент фазы (м-1), связанный с длинной волны в линии передачи λв, круговой частотой
=α+jβ - коэффициент распространения для моделируемого типа волны, α- коэффициент затухания (Нп/м), β - коэффициент фазы (м-1), связанный с длинной волны в линии передачи λв, круговой частотой 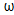 и фазовой скоростью vф соотношением:
и фазовой скоростью vф соотношением:
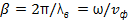 (1.3)
(1.3)
Модули нормированных напряжений и токов падающей и отраженной волн в (1.1) - (1.2’) представляют собой квадратные корни из соответствующих мощностей и поэтому имеют одинаковую размерность 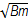 . Фазы нормированных напряжений падающей и отраженной волн принимаются равными фазам поперечных компонентов поля Е для соответствующих волн.
. Фазы нормированных напряжений падающей и отраженной волн принимаются равными фазам поперечных компонентов поля Е для соответствующих волн.
Знак “-“ в (1.2’) для отраженной волной появляется в связи с тем, что ток в длинной линии связан с напряжением соотношением:
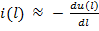 ,
,
и при взятии производной по координате 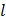 для падающей и отраженной волн из под экспонент в (1.1) и (1.2) выносятся разные знаки.
для падающей и отраженной волн из под экспонент в (1.1) и (1.2) выносятся разные знаки.
При отсутствии в линии омических потерь амплитуда напряжения обеих волн (падающей и отраженной) неизменны в любом сечении тракта.
Отношение поперечных компонентов электрического поля для отраженной и падающей волн в одном и том же поперечном сечении линии передачи называется коэффициентом отражения по электрическому полю 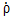 Е= Et 0/ Et п. Так как нормированные напряжения падающей и отраженной волн пропорциональны поперечным компонентам соответствующих электрических полей и имеют одинаковые с ними фазы, то коэффициент отражения для нормированных напряжений
Е= Et 0/ Et п. Так как нормированные напряжения падающей и отраженной волн пропорциональны поперечным компонентам соответствующих электрических полей и имеют одинаковые с ними фазы, то коэффициент отражения для нормированных напряжений 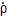 =
= 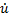 0/
0/ 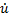 п совпадает с коэффициентом отражения по электрическому полю.
п совпадает с коэффициентом отражения по электрическому полю.
Рассматривая продольные зависимости напряжений падающей и отраженной волн, легко найти закон, по которому изменяется коэффициент отражения при переходе из одного сечения линии в другое:
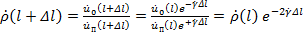 . (1.4)
. (1.4)
где 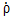 (
(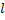 ) - коэффициент отражения в сечении
) - коэффициент отражения в сечении 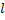 ,
, 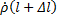 - коэффициент отражения в сечении
- коэффициент отражения в сечении 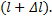
При отсутствии потерь (α=0)
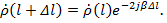 (1.5)
(1.5)
Величина Δ l положительна при смещении от сечения 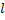 в сторону к генератору и отрицательна при смещении к нагрузке.
в сторону к генератору и отрицательна при смещении к нагрузке.
Из (1.5) следует, что при отсутствии потерь в линии модуль коэффициента отражения не зависит от координаты 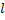 , а фаза меняется от 0 до 2π на интервале, равном половине длины волны в линии.
, а фаза меняется от 0 до 2π на интервале, равном половине длины волны в линии.
Полное напряжение в линии 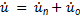 является суперпозицией (наложением) падающей и отраженной волн.
является суперпозицией (наложением) падающей и отраженной волн.
Таким образом, в соответствии со сказанным выше для распространяющейся волны любого типа в линии передачи могут быть формально введены следующие параметры:
1) полное нормированное напряжение в сечении 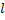 (размерность
(размерность 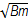 ) в виде суммы нормированных напряжений падающей и отраженной волн:
) в виде суммы нормированных напряжений падающей и отраженной волн:
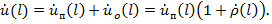 (1.6)
(1.6)
2) полный нормированный ток (размерность 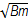 ) в виде разности нормированных напряжений падающей и отраженной волн:
) в виде разности нормированных напряжений падающей и отраженной волн:
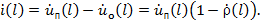 (1.7)
(1.7)
В результате существования двух волн, бегущих навстречу друг другу, в линии устанавливается режим смешанных волн, при этом в разных сечениях линии поля бегущих волн складываются с различной фазой и в продольном распределении напряжения (тока) возникают максимумы и минимумы (рис. 1.1,б).
В пучности (максимуме) напряжение равняется сумме амплитуд падающей и отраженной волн, а в узле (минимуме) – разности:
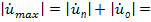
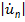 (1+
(1+ 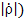
(1.8)
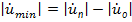
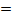
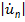 (1
(1 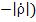
Режим смешанных волн в инженерной практике принято характеризовать величиной коэффициента бегущей волны (КБВ). Под КБВ понимается отношение минимального значения нормированного полного напряжения в линии к его максимальному значению:
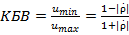 , (1.9)
, (1.9)
Часто вместо КБВ используется обратная ему величина, называемая коэффициентом стоячей волны (КСВ).
При отсутствии в линии омических потерь модуль коэффициента отражения не зависит от продольной координаты 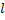 (1.5) и все минимумы и максимумы в продольном распределении напряжения в линии одинаковы. КБВ также постоянен по длине линии.
(1.5) и все минимумы и максимумы в продольном распределении напряжения в линии одинаковы. КБВ также постоянен по длине линии.
Для измерения КБВ (КСВ) применяют специальные приборы - измерительные линии, включаемые в разрыв тракта и позволяющие исследовать картину продольного распределения напряжения в линии с помощью передвижного зонда ([1], Приложение 2).
Кроме того, КБВ (КСВ) можно измерить, включив в тракт так называемые направленные ответвители ([1], Приложение 4), раздельно извлекающие из линии передачи небольшую часть мощности, пропорциональной падающей и отраженной волнам, и тем самым позволяющие измерить амплитуды падающей и отраженной волн.
Мощность, переносимая в линии бегущей волной, может быть вычислена через нормированные токи и напряжения как:
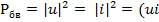 *)
*)
где 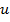 и
и 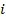 действующие значения напряжения и тока.
действующие значения напряжения и тока.
Date: 2015-07-27; view: 1936; Нарушение авторских прав