Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Круговая номограмма полных сопротивлений (проводимостей)
|
|
В инженерной практике, когда точность определения длин отрезков линий, входящих в проектируемое устройство, не превышает двух значащих цифр, для пересчета сопротивлений (проводимостей) из одного сечения линии передачи в другое, удобно использовать круговую номограмму (диаграмму) полных сопротивлений (проводимостей), называемую также номограммойВольперта или номограммой Вольперта – Смита. В дальнейшем изложении везде будет использоваться термин «круговая номограмма». Стандартный вид диаграммы представлен в Приложении 1.
Идея построения круговой номограммы достаточно проста. Представим на комплексной плоскости (рис. 1.1) коэффициент отражения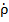 
в векторной форме.
Комплексная величина 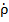изображается точкой на комплексной плоскости с радиусом вектором равным 
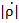. Изменение 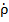при движении по линии от некоторого сечения 
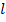, на расстояние Δ 
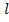описывается в линии без потерь соотношением
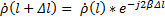
При этом, поскольку потерь в линии нет, модуль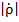 
постоянен по длине линии.
Фаза коэффициента отражения характеризуется углом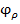 
, отсчитываемым между положительной действительной осью и направлением вектора 
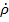. При перемещении к генератору приращение фазы Δφ отрицательно (Δ 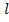>0), а при движении к нагрузке – положительно (Δ 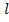<0). Фаза коэффициента отражения меняется на 360о при смещении вдоль линии на расстояние, равное половине длины волны. Направление движения на номограмме обычно указывается стрелками с маркировкой «к нагрузке» и «к генератору».
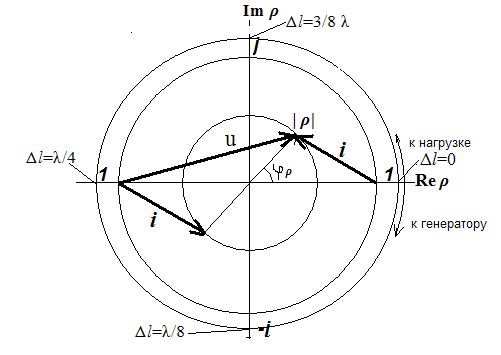
Рис. 1.1 Комплексная плоскость коэффициента отражения
На внешней окружности номограммы c радиусом несколько большим, чем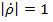 
наносится равномерная шкала расстояний, на которой отмечаются значения Δ 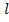в пределах от 0 до λв/2 (как указано выше, 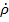периодическая функция с периодом λв/2) и соответствующее величине Δ 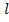значение фазы (4πΔ 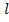/λв) в пределах от 0 до 360 град. При этом, поскольку для пересчета 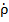из одного сечения линии в другое необходимо знать только разностную величину Δ 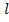, начало отсчета шкалы расстояний может располагаться в любой точке на проградуированной окружности. Стандартно его располагают на действительной оси.
Если теперь на рассматриваемую номограмму в каждой точке нанести величины реальной и мнимой составляющих нормированного сопротивления или проводимости, найденные с использованием соотношений
,
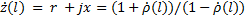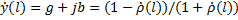
и соединить одинаковые значения непрерывной линией, то получится картина, изображенная на рис.1.2, а и б.
На этих рисунках линии постоянной активной составляющей Re z и Re y изображаются окружностями с центром на горизонтальной оси, имеющими одну общую точку касания (т.2). Внешняя окружность, проходящая через т.1 и т.2, соответствует на представленных номограммах значениям Re z =0 (Re y =0); окружность, проходящая через начало координат соответствует значениям Rez=1 (Rey=1); на горизонтальной оси при движении от т.1 к т.2. Rez и (Rey) меняются от 0 (т.1) до бесконечности (т.2.).
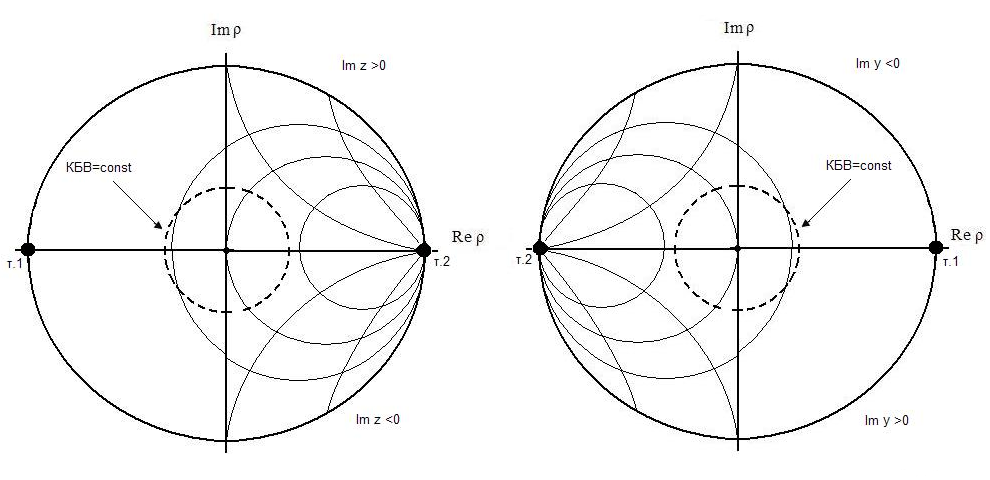
а) б)
Рис. 1.2. а - номограмма сопротивлений; б - номограмма проводимостей
Линии постоянной реактивной составляющей так же являются частями окружностей с центром на вертикальной оси, проходящей через т.2. Знак реактивности выше и ниже действительной оси указан на рис.1.2.
Концентрические окружности с центром в начале координат (одна из которых изображена на номограмме пунктиром) соответствуют линиям постоянного значения модуля коэффициента отражения, но для удобства использования они маркируются величиной КБВ
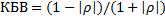
Если представленную на рис.1.2 номограмму сопротивлений повернуть на 90˚ по часовой стрелке, а номограмму проводимостей против часовой стрелки, получится одна и та же по виду номограмма (см. приложение 1). Все маркировки для обеих номограмм полностью совпадают. Поэтому номограмму в повернутом виде можно считать номограммой сопротивлений, если с её помощью предполагается осуществлять пересчет сопротивлений, либо номограммой проводимостей, если будут пересчитываться проводимости.
Основная задача, которую позволяет решить круговая номограмма это пересчет эквивалентных комплексных сопротивлений (проводимостей) из одного сечения линии в другое, не прибегая к прямому использованию соответствующих формул.
Следует отметить, что пересчет сопротивлений (проводимостей) по номограмме может осуществляться только для нормированных величин сопротивлений и проводимостей.
Date: 2015-07-27; view: 2201; Нарушение авторских прав