
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Розділ 6. Статистичне вивчення причинно-наслідкових зв’язків правопорушень
|
|
6.1. Поняття і види взаємозв’язків між правовими ознаками.
6.2. Застосування параметричних методів вимірювання взаємозв’язків у правовій статистиці.
6.3. Оцінювання тісноти зв’язку між правовими ознаками на основі непараметричних статистичних методів.
Питання і завдання для самоконтролю.
6.1. Поняття і види взаємозв’язків між правовими показниками
Явища суспільного життя, в тому числі і правові, тісно пов’язані, залежать одне від одного, і обумовлюють одне одного. Одним з найважливіших завдань статистичної науки, складовою якої є і правова статистика, є вивчення взаємозв’язків між суспільно-правовими явищами та вимірювання причинних залежностей між ними. Серед багатьох форм закономірних взаємозв’язків суспільних явищ важливу роль відіграє причинна залежність, яка означає породження одного правового явища іншим. Але причина сама по собі не визначає наслідку, який залежить від певних умов, що підсилюють дію причини. Тобто для виникнення наслідку необхідний збіг окремих причин і умов. Ознаки, які характеризують причини і умови виникнення певних правових явищ називаються факторними, а ознаки, які характеризують наслідки їх дії — результативними. До юридичних наук, які вивчають причинні залежності, передусім належить кримінологія — наука про злочинність і її причини, а також кримінальне право, яке встановлює причинний зв’язок між діяннями та їх наслідками з погляду настання кримінальної відповідальності за скоєне. Певні криміногенні фактори — пиятство, бродяжництво, проституція, наркоманія (причини) визначають відповідний рівень злочинності (наслідок).
Будь-який закономірний взаємозв’язок передбачає повторюваність, послідовність і порядок в правових явищах і процесах, але проявляється по-різному. За статистичною природою взаємозв’язки поділяються на функціональні та стохастичні. У разі функціонального зв’язку зміна результативної ознаки цілком визначається зміною однієї або кількох факторних ознак, тобто спостерігається повна відповідність між причинами і наслідком. Функціональний зв’язок виражається точною математичною формулою, яка характерна для будь-якого випадку, а тому найчастіше зустрічається в математиці, фізиці, хімії і інших природничих науках. У правових явищах функціональну залежність відшукати складно.
Соціально-правові явища і процеси — це результат одночасної взаємодії великої кількості причин і умов, а тому їм характерні стохастичні зв’язки. При стохастичному зв’язку кожному значенню факторної правової ознаки відповідає певна множина значень результативної правової ознаки. Звідси при фіксованому значенні факторної правової ознаки дістаємо розподіл елементів сукупності за результативною правовою ознакою, який називається умовним. Отже, стохастичний зв’язок виявляється в тому, що зі зміною значень факторної ознаки змінюється умовний розподіл правових явищ за результативною ознакою.
Окремим випадком стохастичної залежності є кореляційна, яка полягає в тому, що зі зміною факторної правової ознаки змінюються середні значення результативної правової ознаки. Наприклад, залежність між аварійністю автотранспорту і професіоналізмом водіїв: зі збільшенням стажу роботи водієм знижується середня кількість аварій автотранспорту. Або залежність між рецидивом судимості і часом перебування на свободі: зростання кількості судимостей у злочинця призводить до скорочення часу перебування на свободі і т. ін.
Для встановлення кореляційного зв’язку між наведеними правовими явищами необхідно взяти достатньо велику їхню кількість (водіїв чи рецидивістів), і дослідити середні значення результативних правових показників. Завдання кореляційної залежності полягає в тому, щоб за допомогою математичних прийомів встановити кількісну характеристику цієї залежності, абстрагуючись при цьому від впливу інших факторних правових ознак. Проте кореляційний аналіз не тільки виявляє наявність зв’язку між правовими явищами, але й установлює форму та тісноту зв’язку, подає кількісну оцінку впливу факторної правової ознаки на результативну.
За напрямом зв’язку між правовими явищами кореляційні зв’язки поділяються на прямі і обернені. Між криміногенними факторами і злочинністю існує прямий кореляційний зв’язок, бо зростання впливу цих факторів призводить до зростання рівня злочинності. Наприклад, чим поширеніший алкоголізм в суспільстві, тим вищий рівень злочинності у стані алкогольного сп’яніння. Якщо зі збільшенням факторної правової ознаки результативна правова ознака зменшується і навпаки, то йдеться про обернений кореляційний зв’язок. Наприклад, чим вищий рівень соціального контролю злочинності в суспільстві, тим нижчий її рівень.
За аналітичним вираженням прямі і обернені кореляційні зв’язки можуть бути прямолінійними і криволінійними. При прямолінійному зв’язку відбувається рівномірне зростання або зменшення результативної правової ознаки під впливом збільшення значень факторної правової ознаки. Зв’язок такого виду математично виражається лінійним рівнянням регресії. При криволінійному зв’язку зростання факторної правової ознаки призводить до нерівномірної зміни результативної правової ознаки. Прикладом криволінійному зв’язку може бути залежність злочинності від віку злочинців. На початку віку, з якого настає кримінальна відповідальність, і далі, приблизно до 30 років, кримінальна активність правопорушників зростає, а потім знижується. При цьому в динаміці кримінальна активність молодшає.
За кількістю факторних правових ознак прямолінійні кореляційні зв’язки можуть бути однофакторними (парними) і багатофакторними. Зв’язок між однією факторною ознакою і однією результативною правовою ознакою називається однофак-торним, або парним. Залежність результативної правової ознаки від двох і більше факторних ознак вважається багатофакторним кореляційним зв’язком. При цьому виділяється частинний зв’язок, який полягає в залежності результативної правової ознаки від однієї факторної ознаки при фіксованих значеннях інших правових ознак.
Статистичне вивчення зв’язку між правовими ознаками проходить декілька етапів. На першому етапі проводиться якісний аналіз правового явища, пов’язаний зі встановленням його соціально-правової природи; далі передбачається модель зв’язку, визначається її тип і тільки після цього подається кількісна характеристика цієї залежності, пов’язана з якісними його особливостями.
Уявлення про залежність злочинності від інших соціальних факторів дозволяє пояснити її причини, кількісно описати зміни, які в ній відбуваються, а також розробляти необхідні заходи соціального контролю над нею.
6.2. Застосування параметричних методів вимірювання взаємозв’язків у правовій статистиці
Для кількісної характеристики залежності між правовими ознаками найбільш досконалим і надійним є метод кореляційно-регресійного аналізу, який передбачає застосування основних параметрів розподілу — середніх показників і дисперсій, а тому його називають параметричним методом вимірювання взаємозв’язків.
Реалізація методу кореляційно-регресійного аналізу передбачає послідовне виконання таких етапів:
1) теоретичне обґрунтування взаємозв’язку між правовими ознаками;
2) оцінювання лінії регресії;
3) вимірювання тісноти зв’язку;
4) перевірка істотності виявленого зв’язку.
В основу кореляційно-регресійного аналізу покладено припущення, що залежність між значеннями факторної правової ознаки і результативною правовою ознакою може бути виражена деякою функцією: Y = f (x), яка називається рівнянням регресії; Y — це теоретичні значення результативної правової ознаки, обчислені за цим рівнянням; у — фактичні значення результативної правової ознаки.
Залежність між правовими ознаками за аналітичним виразом може бути прямолінійною і криволінійною, а тому її можна описати регресійними рівняннями різного виду:
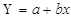 — лінійне;
— лінійне;
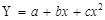 — параболічне;
— параболічне;
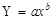 — степеневе;
— степеневе;
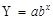 — показникове;
— показникове;
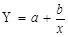 — гіперболічне.
— гіперболічне.
На етапі теоретичного обґрунтування взаємозв’язку відбувається вибір факторних правових ознак та визначення функціонального виду регресійного рівняння. Для обґрунтування останнього використовуються такі прийоми:
1. Якісний теоретичний аналіз суті взаємозв’язку між правовими ознаками. Якщо, наприклад, рівномірне зростання кількості спожитого алкоголю на душу населення призводить до пропорційного зростання кількості зареєстрованих злочинів у стані алкогольного сп’яніння, то зв’язок між цими правовими ознаками можна описати лінійним рівнянням. Або, якщо зі збільшенням віку засуджених до певної межі (до 30 років) рівень судимості зростає, а потім знижується, то такий зв’язок описується параболою і т. д.
2. Графічний аналіз зв’язку між правовими ознаками за допомогою кореляційного поля. При його побудові на осі абсцис відкладається значення факторної правової ознаки х, а на осі ординат — результативної правової ознаки у. Кожному елементу сукупності на графіку відповідає окрема точка. За розміщенням точок на кореляційному полі робиться висновок про характер зв’язку між правовими ознаками.
Якщо точки безладно розкидані по кореляційному полю, то будь-якого зв’язку між ознаками немає. Якщо вони зосереджені у напрямку знизу—вгору зліва—направо, то виконується пряма залежність, а якщо точки розподілені зверху-вниз і зліва-направо, то залежність між ознаками буде оберненою.
3. Перебір функцій, коли обчислюються різні види регресійних рівнянь, а потім за відомим критеріями (середня квадратична помилка) вибирається те, яке найкраще відповідає фактичним даним.
На етапі оцінки лінії регресії після визначення форми регресійного рівняння обчислюються його параметри методом найменших квадратів. Основна умова цього методу полягає в тому, що сума квадратів відхилень фактичних значень результативної правової ознаки (у) від теоретичних (Y) повинна бути мінімальною: å(y – Y)2 = min. Це дає змогу дістати найкращі оцінки регресійних параметрів. Для їх обчислення треба скласти і розв’язати систему нормальних рівнянь. Лінійній формі зв’язку y = a + bx відповідає така система:
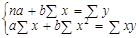 .
.
Розв’язання цієї системи дозволяє отримати параметри лінійного регресійного рівняння а і b. Параметр а — це теоретичне значення результативної ознаки 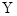 для х = 0. Якщо х = 0 міститься в межах фактичної варіації факторної ознаки, то а — одне з теоретичних значень
для х = 0. Якщо х = 0 міститься в межах фактичної варіації факторної ознаки, то а — одне з теоретичних значень 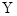 , якщо ознака х не набуває нульового значення, то параметр а не має реального змісту і використовується лише для розрахунків. Параметр b називається коефіцієнтом регресії і показує, наскільки одиниць власного виміру змінюється в середньому значення результативної правової ознаки зі збільшенням значення факторної ознаки на одиницю також власного виміру.
, якщо ознака х не набуває нульового значення, то параметр а не має реального змісту і використовується лише для розрахунків. Параметр b називається коефіцієнтом регресії і показує, наскільки одиниць власного виміру змінюється в середньому значення результативної правової ознаки зі збільшенням значення факторної ознаки на одиницю також власного виміру.
Мірою тісноти зв’язку між правовими ознаками будь-якої форми є коефіцієнт детермінації, що обчислюється як співвідношення факторної і загальної дисперсій: 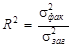 . Коефіцієнт детермінації характеризує частку варіації результативної правової ознаки, яка пов’язана з факторною ознакою при відповідній формі зв’язку. Коефіцієнт детермінації змінюється від 0 до 1. При
. Коефіцієнт детермінації характеризує частку варіації результативної правової ознаки, яка пов’язана з факторною ознакою при відповідній формі зв’язку. Коефіцієнт детермінації змінюється від 0 до 1. При 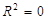 зв’язок між х та у відсутній, при
зв’язок між х та у відсутній, при 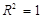 — функціональний.
— функціональний.
Корінь квадратичний з коефіцієнта детермінації називають індексом кореляції: 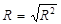 .
.
Тіснота лінійного зв’язку між правовими ознаками вимірюється за допомогою лінійного коефіцієнта кореляції r:
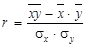 ,
,
де 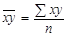 ;
; 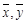 — середні значення відповідно факторної х та результативної у правової ознаки:
— середні значення відповідно факторної х та результативної у правової ознаки: 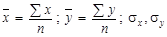 — середні квадратичні відхилення факторної та результативної правової ознаки:
— середні квадратичні відхилення факторної та результативної правової ознаки: 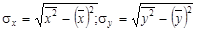 .
.
Лінійний коефіцієнт кореляції можна обчислювати до розрахунку параметрів регресійного рівняння. Він коливається в межах від –1 до +1 і характеризує не тільки тісноту, а й напрям зв’язку між ознаками. Додатне значення r означає прямий зв’язок, від’ємне — зворотний. Абсолютна величина лінійного коефіцієнта кореляції збігається з індексом кореляції для лінійної форми зв’язку: 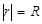 .
.
Щоб зробити висновок про ступінь тісноти зв’язку між правовими ознаками, їх треба порівняти з такими критеріями оцінки тісноти зв’язку: до 0,3 — зв’язок слабкий; 0,3—0,5 — помітний; 0,5—0,7 — помірний; 0,7—0,9 — тісний; 0,9—0,99 — дуже тісний.
Перевірка істотності зв’язку в кореляційно-регресійному аналізі здійснюється за допомогою критерія Фішера: 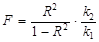 , де
, де 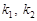 — кількість ступенів вільності, яке залежить від кількості параметрів регресійного рівняння;
— кількість ступенів вільності, яке залежить від кількості параметрів регресійного рівняння; 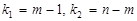 , де n — кількість елементів сукупності, а m — число параметрів в рівнянні регресії.
, де n — кількість елементів сукупності, а m — число параметрів в рівнянні регресії.
Перевірка істотності зв’язку ґрунтується на порівнянні фактичного значення критерію Фішера з критичним його значенням для заданого рівня ймовірності. Критичні (табличні) значення — це максимально можливі значення критерія, які можуть виникнути випадково за відсутності кореляційного зв’язку. Вони залежать від кількості ступенів вільності (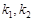 ) та рівня істотності (
) та рівня істотності (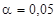 і
і 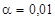 ). Якщо фактичне значення критерія Фішера F більше від критичного
). Якщо фактичне значення критерія Фішера F більше від критичного 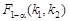 , тобто
, тобто 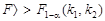 , то зв’язок між х та у істотний, якщо
, то зв’язок між х та у істотний, якщо 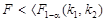 , то істотність зв’язку не доведена. У статистичній літературі існують таблиці критичних значень F -критерію [16, с. 112].
, то істотність зв’язку не доведена. У статистичній літературі існують таблиці критичних значень F -критерію [16, с. 112].
Наприклад, за даними вибіркового обстеження 10 регіонів про рівень споживання алкогольних напоїв на душу населення та кількість зареєстрованих хуліганств у стані алкогольного сп’яніння на 100 тис. населення здобуто такі результати:
| Номер регіону | ||||||||||
| Споживання алкоголю, л | 3,3 | 3,8 | 2,4 | 3,1 | 2,7 | 3,2 | 3,5 | 3,6 | 3,0 | 2,8 |
| Кількість хуліганств |
Щоб проаналізувати залежність між цими ознаками, передусім слід встановити форму зв’язку між ними. Теоретичний аналіз залежності, яка простежується за первинними даними, показує, що зростання кількості спожитого алкоголю на душу населення спричиняє зростання кількості зареєстрованих хуліганств у стані алкогольного сп’яніння.
Для підтвердження встановленої залежності побудуємо кореляційне поле, на якому зобразимо факторну ознаку х — споживання алкогольних напоїв на душу населення на осі абсцис, а результативну ознаку у — кількість зареєстрованих хуліганств — на осі ординат (рис. 6.1).
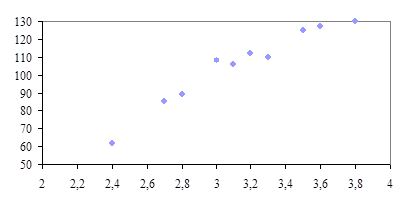
Рис. 6.1. Кореляційне поле залежності кількості зареєстрованих
хуліганств у стані алкогольного сп’яніння від споживання
алкогольних напоїв на душу населення
По розміщенню точок на кореляційному полі також можна зробити висновок, що залежність між факторною і результативною ознакою лінійна і виражається регресійним рівнянням виду 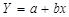 .
.
Для обчислення параметрів а і b будується наведена вище система нормальних рівнянь, необхідні суми для якої визначаються в табл. 6.1.
Таблиця 6.1
Date: 2015-07-27; view: 558; Нарушение авторских прав