
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Метод узловых потенциалов
|
|
Ток в любой ветви схемы можно найти по обобщенному закону Ома. Для того, чтобы можно было применить закон Ома, необходимо знать значение потенциалов узлов схемы. Метод расчета электрических цепей, в котором за неизвестные принимают потенциалы узлов схемы, называют методом узловых потенциалов. Число неизвестных в методе узловых потенциалов равно числу уравнений, которые необходимо составить для схемы по I закону Кирхгофа. Метод узловых потенциалов, как и метод контурных токов, – один из основных расчетных методов. В том случае, когда п- 1 < p (n – количество узлов, p – количество независимых контуров), данный метод более экономичен, чем метод контурных токов.
Проиллюстрируем на простом примере получение методики расчета электрической цепи методом узловых потенциалов:
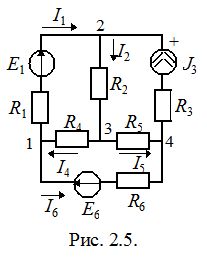
|
1. Записываем (n – 1) уравнение по I закону Кирхгофа (при выбранном опорном узле 4, потенциал которого условно принимаем равным нулю)
узел 1: – I1 + I4 - I6 = 0
узел 2: I1 – I2 + J3 = 0
узел 3: I2 – I4 + I5 = 0
2. Для каждого из m токов записываем выражение по обобщенному закону Ома через потенциалы узлов с учетом, что потенциал j4 = 0:
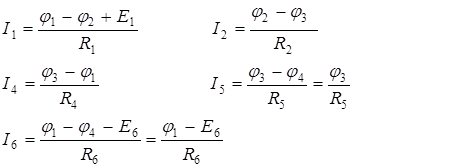
3. Полученные в п. 2 выражения подставляем в уравнения, составленные по I закону Кирхгофа
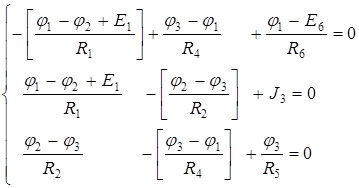
Приведем подобные слагаемые при различных потенциалах и получим каноническую систему уравнений:
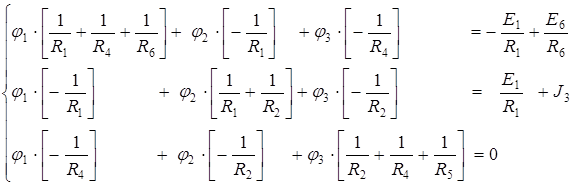 (2.10)
(2.10)
Введем обозначения:
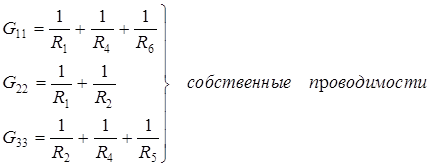
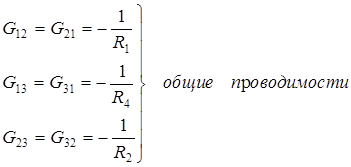
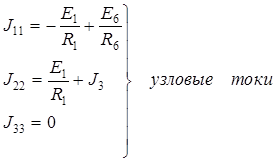
В окончательном виде система уравнений для контурных токов приобретает следующий вид:
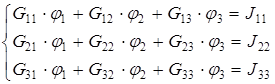 (2.11)
(2.11)
в матричной форме
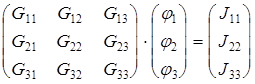 (2.12)
(2.12)
Собственная проводимость узла (G ii ) представляет собой арифметическую сумму проводимостей всех ветвей, соединенных в i -ом узле.
Общая проводимость i-ого и j-ого узлов (G ij = G ji ) представляет собой взятую со знаком «–» сумму проводимостей ветвей, присоединенных одновременно к i- ому и j- ому узлам.
Проводимости ветвей с источниками тока полагаются равными нулю и в собственные и общие проводимости не входят!
Узловой ток (J ii ) состоит из двух алгебраических сумм: первая содержит токи источников тока, содержащиеся в ветвях, соединенных в i -ом узле; вторая представляет собой произведение ЭДС источников напряжения на проводимости соответствующих ветвей, соединенных в i -ом узле. Со знаком «+» в эту сумму входят E и J источников, действие которых направлено к узлу, со знаком «–» остальные.
Решение системы уравнений по методу узловых потенциалов в общем случае выполняется методом Крамера при помощи определителей:
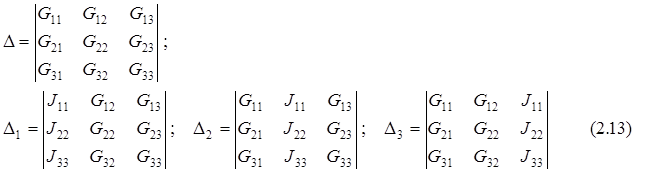
Тогда неизвестные потенциалы могут вычислены следующим образом:
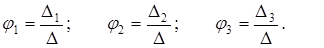 (2.14)
(2.14)
Нетрудно, показать, что аналогичную систему уравнений можно построить для случая n узлов в цепи. Тогда необходимо составить для (n- 1 ) узлов соответствующие уравнения, полагая потенциал n -ого узла, равным нулю.
Таким образом, методика расчета цепи постоянного тока методом узловых потенциалов следующая:
1. Обозначить все токи ветвей и их положительное направление.
2. Произвольно выбрать опорный узел (jn) и пронумеровать все остальные (n- 1) -e узлы.
3. Определить собственные и общие проводимости узлов, а также узловые токи, т.е. рассчитать коэффициенты в системе уравнений.
4. Записать систему уравнений в виде
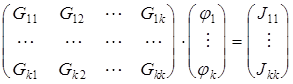 – матричная форма
– матричная форма
Или в развернутом виде:
алгебраическая форма
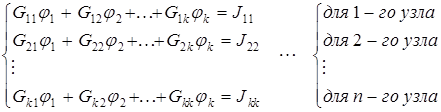
В этой системе каждому узлу соответствует отдельное уравнение.
5. Полученную систему уравнений решить относительно неизвестных (n – 1) потенциалов при помощи метода Крамера.
6. С помощью обобщенного закона Ома рассчитать неизвестные токи.
7. Проверить правильность расчетов при помощи баланса мощности.
Порядок расчета не зависит от вида источников, действующих в цепи. Однако, расчет упрощается в случае, когда между одной или несколькими парами узлов включены идеализированные источники ЭДС. Тогда напряжения между этими парами узлов становятся известными величинами, определенными условиями задачи. Для успешного решения подобных задач необходимо правильно обозначить опорный узел, в качестве которого может быть выбран только один из узлов, к которым присоединена ветвь с идеализированным источником ЭДС.
Если таких ветвей q, то количество уравнений в системе сократится до
k = n – 1 – q.
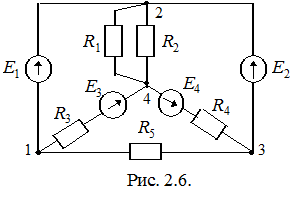
Пример.
Если в данной схеме в качестве опорного узла выбрать узел 1 (j 1=0), то потенциалы второго и третьего узлов можно считать известными и равными соответственно j 2 =E 1 и j 3 =E 1 –E 2. Тогда неизвестным остается только потенциал четвертого узла, для которого составим уравнение по методу узловых потенциалов:
|
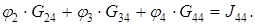
Следует отметить, что уравнения для 2 и 3 узлов составить не представляется возможным из-за появляющихся неопределенностей вида 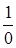 , т.к. сопротивление ветви, содержащей идеализированный источник ЭДС, равно нулю, а проводимость соответственно
, т.к. сопротивление ветви, содержащей идеализированный источник ЭДС, равно нулю, а проводимость соответственно 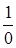 .
.
Подставим известные значения:
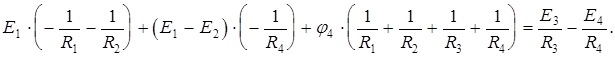
Из полученного уравнения найдем неизвестный 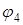 , а далее и все токи.
, а далее и все токи.
Для разветвленной цепи, имеющей только два узла и произвольное количество ветвей, метод узловых потенциалов вырождается в метод двух узлов. Решение сводится к отысканию значения потенциала одного из узлов, т.к. потенциал другого узла может быть принятым равным нулю.
Система уравнений превращается в одно уравнение:
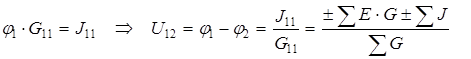 (2.15)
(2.15)
при условии, что 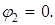
После определения U 12 токи ветвей и напряжения источников тока находят при помощи обобщенного закона Ома.
Пример.
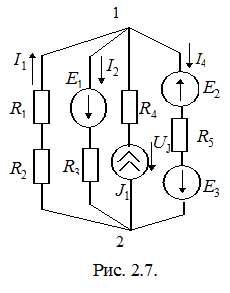
|
Пусть 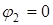 , тогда
, тогда
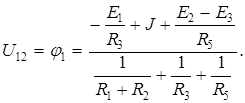
По обобщенному закону Ома:
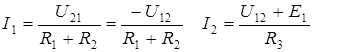
Date: 2015-07-27; view: 1200; Нарушение авторских прав