Метод контурных токов

Метод контурных токов является одним из основных методов расчета сложных электрических цепей, которым широко пользуются на практике.

При расчете методом контурных токов полагают, что в каждом независимом контуре течет свой контурный ток. Уравнения составляют относительно контурных токов, после чего определяют токи ветвей через контурные токи.

Таким образом, метод контурных токов можно определить как метод расчета, в котором за искомые принимают контурные токи. Число неизвестных в этом методе равно числу уравнений, которые необходимо было бы составить для схемы по II закону Кирхгофа, т.е. 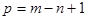. Следовательно, этот метод более экономичен при вычислениях, чем метод уравнений Кирхгофа.

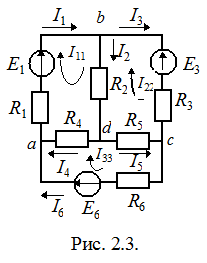
Разработаем алгоритм расчета цепей методом контурных токов на примере приведенной на рис. 2.3. схемы, в которой три независимых контура. Предположим, что в каждом контуре протекает свой контурный ток в указанном направлении. Для каждого из контуров составим уравнения по II закону Кирхгофа. При этом учтем, что по смежной ветви для контурных токов 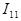и 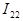(ветвь bd, содержащая сопротивление 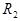) протекает ток 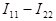, по смежной ветви для контурных токов 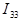и 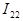(ветвь dс, содержащая сопротивление 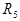) протекает ток 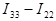, по смежной ветви для контурных токов 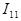и 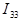(ветвь аd, содержащая сопротивление 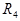) протекает ток .

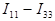Тогда уравнения по II закону Кирхгофа для каждого контура принимают следующий вид:

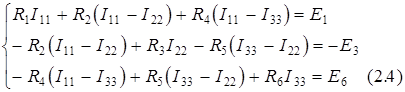Сгруппируем слагаемые при одноименных токах:

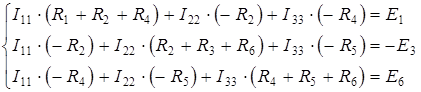(2.5)

Введем обозначения:

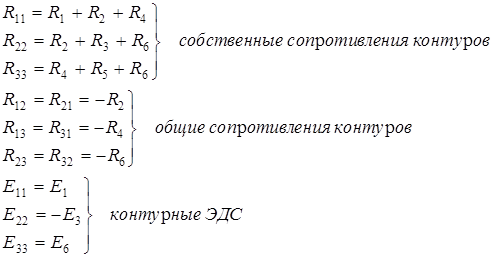
В окончательном виде система уравнений для контурных токов приобретает следующий вид:

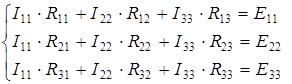(2.6)

в матричной форме

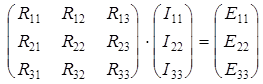(2.7)

Собственное сопротивление контура (R _ii ) представляет собой арифметическую сумму сопротивлений всех потребителей, находящихся в i -ом контуре.

Общее сопротивление контура (R _ij = R _ji ) представляет собой алгебраическую сумму сопротивлений потребителей ветви (нескольких ветвей), одновременно принадлежащих i -ому и j -ому контурам. В эту сумму сопротивление входит со знаком «+», если контурные токи протекают через данное сопротивление в одном направлении (согласно), и знак «–», если они протекают встречно.

Контурные ЭДС представляют собой алгебраическую сумму ЭДС источников, входящих в контур. Со знаком «+» в эту сумму входят ЭДС источников, действующих согласно с обходом контура, со знаком «–» входят ЭДС источников, действующих встречно.

Решение полученной системы удобно выполнить методом Крамера

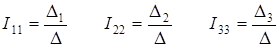, (2.8)

где D, D₁, D₂, D₃, – соответственно определители матриц:

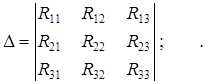
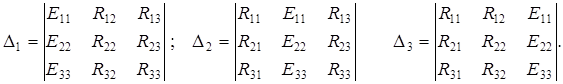(2.9)

По найденным контурным токам при помощи I закона Кирхгофа определяются токи ветвей.

Таким образом, методика расчета цепи постоянного тока методом контурных токов следующая:

1. Обозначить все токи ветвей и их положительное направление.

2. Произвольно выбрать совокупность p независимых контуров, нанести на схему положительное направление контурных токов, протекающих в выбранных контурах.

3. Определить собственные, общие сопротивления и контурные ЭДС и подставить их в систему уравнений вида (2.3).

4. Разрешить полученную систему уравнений относительно контурных токов, используя метод Крамера.

5. Определить токи ветвей через контурные токи по I закону Кирхгофа.

6. В случае необходимости, с помощью обобщенного закона Ома определить потенциалы узлов.

7. Проверить правильность расчетов при помощи баланса мощности.

Если в цепи содержится q источников тока, количество совместно рассматриваемых уравнений сокращается на q и становится равным р – q, поскольку токи в таких ветвях известны (для контуров с I _ii = J уравнение можно не записывать). В этом случае следует выбирать такую совокупность независимых контурных токов, чтобы часть из них стала известными. Для этого необходимо, чтобы каждый источник тока входил только в один контур. Напряжения U _J источников войдут в качестве неизвестных в правые части уравнений, т.е. в состав контурных ЭДС.

Пример.

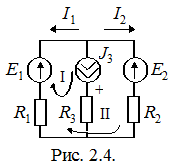
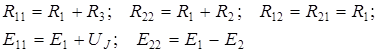
Тогда система уравнений по методу контурных токов примет следующий вид:

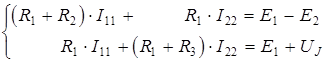
Причем, 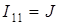, решив первое уравнение, можно получить 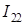. Далее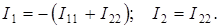

U_J можно определить из второго уравнения системы или, составив уравнение по II закону Кирхгофа для любого контура, в который входит источник тока.

Баланс мощности:

Date: 2015-07-27; view: 1115; Нарушение авторских прав