Расчет разветвленных цепей с одним источником

Разветвленную цепь с одним источником обычно упрощают, преобразуя в неразветвленную (рис. 2.1.), и решают методами, изложенными выше. Основная проблема состоит в нахождении токов и напряжений ветвей исходной схемы, поскольку в результате преобразования такие ветви не сохраняются.

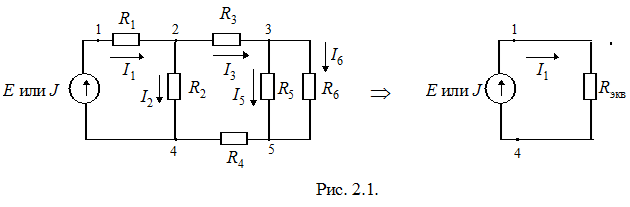
Для определения токов и напряжений в схеме рис. 2.1. сначала определяется R_экв смешанного соединения потребителей относительно зажимов источника (точки 1 и 4 на рис. 2.1.). Затем, если цепь питается источником напряжения, то определяется ток по формуле:

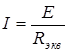
Если цепь питается источником тока, то определяется напряжение

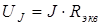
Порядок дальнейшего расчета одинаков для обоих случаев, т.к. известны E или U_J и I или J неразветвленной части схемы. Рассмотрим порядок расчета для представленной на рис. 2.1 цепи.

Ток в потребителе R₁ совпадает с найденным током неразветвленной части I, а напряжение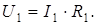

.

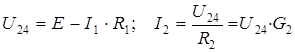Ток I₃ определяется по закону Кирхгофа: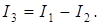

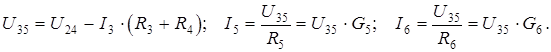
Указанный прием используется и в тех случаях, когда для упрощения цепи приходится прибегать к преобразованию «треугольник ® звезда» или «звезда ® треугольник». Недостаток заключается в том, что цепь приходится рассчитывать дважды – преобразованную и исходную.

При расчетах удобно пользоваться формулой о токах в двух параллельных пассивных ветвях. Выведем ее на примере схемы рис. 2.1. Напряжение 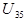по закону Ома определяется по формуле

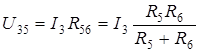
Тогда ток 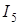можно определить

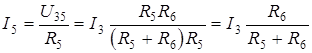(2.2)

Аналогично можно определить ток

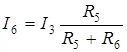(2.3)

Таким образом, ток в одной из двух параллельных ветвей равен току неразветвленной части (общей ветви), умноженному на сопротивление противоположной ветви, деленному на сумму сопротивлений обеих ветвей.

Известен еще один метод расчета таких цепей – метод пропорциональных величин. Он применим к «удлиненным» цепям (цепным соединениям).

Суть этого метода состоит в следующем: в ветви наиболее удаленной от источника (R₆) задаются некоторым значением тока или напряжения. Для удобства расчетов обычно это 1А или 1В. Затем перемещаясь к началу цепи определяют поочередно токи и напряжения всех ветвей вплоть до ветви, содержащей источник. Тем самым определяют какие напряжение U_вх и ток I_вх. должен иметь источник для того, чтобы вызвать во всех ветвях токи и напряжения вычисленных значений. Если ЭДС (Е) или задающий ток (J) с этими значениями не совпадают, то необходимо пропорционально изменить вычисленные значения токов и напряжений ветвей путем умножениях их на отношение или .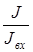

Для схемы на рис. 2.1. пусть I₆ = 1. Тогда

I₃ можно определить по I закону Кирхгофа: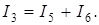

U₂₄ определяем по II закону Кирхгофа: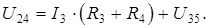

По закону Ома: 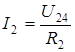, по I закону Кирхгофа: .

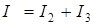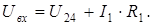
Коэффициент пересчета определяется следующим образом: 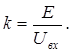Все рассчитанные значения токов и напряжений необходимо домножить на коэффициент k.

Date: 2015-07-27; view: 135; Нарушение авторских прав