Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Числовые выражения. Изучение правил порядка
|
|
Тема 20. Методика изучения алгебраического материала
План
1. Основные понятия математики.
2. Общие вопросы методики изучения алгебраического материала в курсе математики начальных классов.
3. Числовые выражения. Изучение правил порядка выполнения арифметических действий.
4. Выражения с переменной. Уравнения в начальном курсе математики.
5. Методика изучения числовых равенств и числовых неравенств
Основные понятия математики
Числовое выражение в общем виде можно определить так:
1) Каждое число является числовым выражением.
2) Если А и B - числовые выражения, то (А)+(В), (А) - (В), (А)×(В); (А):(В); (А)(В) и f (А) где f (x) - некоторая числовая функция) тоже являются числовыми выражениями.
Если в числовом выражении можно выполнить все указанные в нем действия, то полученное в результате действительное число называют числовым значением данного числового выражения, а о числовом выражении говорят, что оно имеет смысл. Иногда числовое выражение не имеет числового значения, т.к. не все указанные в нем действия выполнимы; о таком числовом выражении говорят, что оно не имеет (лишено) смысла. Так, следующие числовые выражения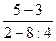 
; 
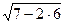и (7-7)0 не имеют смысла.
Таким образом, любое числовое выражение либо имеет одно числовое значение, либо лишено смысла.
Принят следующий порядок действий при вычислении значения числового выражения:
1. Сначала выполняются все операции внутри скобок. Если имеется несколько пар скобок, вычисления начинаются с самых внутренних.
2. Внутри скобок порядок вычислений определяется приоритетом операций: первыми вычисляются значения функций, затем выполняется возведение в степень, потом - умножение или деление, и последними - сложение и вычитание.
3. При наличии нескольких операций одного приоритета вычисления выполняются последовательно слева направо.
Числовое равенство - два числовых выражения A и B, соединенных знаком равенства («=»).
Числовое неравенство - два числовых выражения A и B, соединенных знаком неравенства («<», «>», «≤» или «≥»).
Выражение, содержащее переменную и обращающееся в числовое выражение при замене переменной ее значением, называется выражением с переменной или числовой формой.
Уравнение с одной переменной (с одним неизвестным) - предикат вида f 1(x) = f 2(x), x Î X, где f 1(x) и f 2(x) - выражения с переменной x, определенные на множестве X.
Всякое значение переменной x из множества X, при котором уравнение обращается в верное числовое равенство, называется корнем (решением) уравнения. Решить уравнение - это значит найти все его корни или доказать, что их нет. Множество всех корней уравнения (или множество истинности T предиката f 1(x) = f 2(x), x Î X) называют множеством решений уравнения.
Множество значений x, при которых определены обе части уравнения, называют областью допустимых значений (ОДЗ) переменной x или областью определения уравнения.
Общие вопросы методики изучения алгебраического материала
Начальный курс математики наряду с основным арифметическим материалом включает в себя и элементы алгебры, представленные следующими вопросами:
- числовые выражения;
- выражения с переменной;
- числовые равенства и неравенства;
- уравнения.
Целью включения элементов алгебры в курс математики начальных классов является:
- более полно и более глубоко рассматривать арифметический материал;
- доводить обобщения учащихся до более высокого уровня;
- создать предпосылки для более успешного изучения алгебры в среднем и старшем звене школы.
К элементам алгебры, включенным в курс математики начальных классов, относятся следующие вопросы:
- числовые выражения;
- выражения с переменной;
- числовые равенства и числовые неравенства;
- уравнения;
- неравенства с переменной.
Алгебраический материал не выделен в программе отдельной темой. Он распределен по всему курсу математики начальных классов отдельными вопросами. Изучаются эти вопросы, начиная с 1 класса, параллельно с изучением основного арифметического материала. Последовательность рассмотрения предложенных программой вопросов определяется учебником.
Усвоение изучаемых алгебраических понятий в начальных классах предполагает введение соответствующей терминологии и выполнение простейших операций без построения формально логических определений.
Числовые выражения. Изучение правил порядка
Date: 2015-08-15; view: 2217; Нарушение авторских прав