II. Квадратные уравнения с параметром и уравнения, приводимые к квадратным

В таких уравнениях в качестве «контрольных» берут обычно значения параметра, обращающие в нуль коэффициент при х ², так как в этом случае уравнение становится линейным, а также значение параметра, обращающие в нуль дискриминант уравнения, так как от значения дискриминанта зависит число действительных корней квадратного уравнения.

Пример 5. Решить уравнение с параметром

(а –1) х ²+2(2 а +1) х +(4 а +3) = 0

1. Найдем значения параметра, обращающие в нуль коэффициент при х

а– 1=0 Û а= 1

2. Решим уравнение при а= 1

0× х ²+2(2×1+1) х +4×1+3=0 Û 6 х +7=0 Û .

3. Найдем значения параметра, обращающие в нуль дискриминант уравнения

D =(2(2 а +1))²–4(а –1)(4 а +3)=(4 а +1)²–(4 а –4)(4 а +3)=4(5 а +4)

4(5 а +4)=0 Û .

4. Решим уравнение при , в этом случае уравнение будет иметь один действительный корень

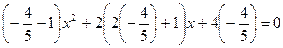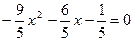Û Û

9 х ²+6 х +1=0 Û (3 х +1)²=0 Û .

5. Решим уравнение при а ¹1, 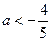. В этом случае D <0, поэтому уравнение действительных корней не имеет.

6. Решим уравнение при а ¹1, . В этом случае уравнение имеет два действительных корня

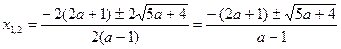
7. Ответ: 1) при , ;

2) при а= 1, ;

3) при 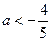, действительных корней нет;

4) при и а ¹1, .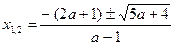

Приведем алгоритм решения задач этого типа.

1. Найти значения параметров и неизвестной, при которых уравнение не имеет смысла (если, конечно, такие есть).

2. Привести уравнение к стандартному виду квадратного уравнения (если это необходимо).

3. Найти «контрольные» значения параметра, обращающие в нуль коэффициент при х ².

4. Решить уравнение при этих значениях а, проверить, все ли найденные корни соответствуют п.1.

5. Найти «контрольные» значения параметра, обращающие в нуль дискриминант уравнения и найти корни уравнения при этом значении параметра, после чего проверить удовлетворяют ли они п.1.

6. Записать корни уравнения при значениях параметра, для которых D> 0, проверить, удовлетворяют ли они п.1.

7. Записать ответ.

Пример 6. Решить уравнение с параметром

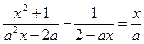
1. Так как а стоит в знаменателе дроби, то уравнение имеет смысл только при а ¹0. В знаменателе стоят и выражения а²х– 2 а и 2– ах, которые тоже должны быть отличны от нуля

а²х– 2 а ¹0 Û а (ах –2)¹0 Û а ¹0, ах –2¹0 Û а ¹0, ;

2– ах ¹0 Û .

Таким образом, мы видим, что .

2. Решим уравнение при а ¹0,

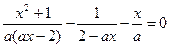Û Û

(1– а) х ²+2 х +1+ а =0...................(*)

3. Найдем значения параметра, обращающие в нуль коэффициент при х ²

1– а =0 Û а =1

4. Решим уравнение (*) при а =1

0× х ²+2 х +2=0 Û 2 х=– 2 Û х= –1

сразу проверим, не совпадает ли х с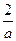

а =1 Þ 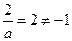, значит, при а =1, х=– 1.

5. Найдем значение параметра, обращающего в нуль дискриминант уравнения (*)

D= 4–4(1– а)(1+ а)=4–4(1– а ²)=4 а ²

4 а ²=0 Û а =0,

но при этом значении параметра уравнение не имеет смысла.

Замечаем, что так как D= 4 а ²>0 при любом значении а ¹0, поэтому уравнение (*) имеет два действительных корня при а ¹1, найдем их

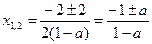Þ .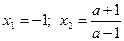

Проверим, чтобы

корень уравнения при а ¹–2.

Найдем чему равен х ₂ при а= –2

_.

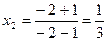a ²– a– 2 = 0, а это уравнение не имеет действительных корней, то есть

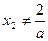ни при каком а ¹1.

6. Ответ: 1) а =0 уравнение не имеет смысла;

2) а =1, х=– 1;

3) а¹ 0, а¹ –2, ;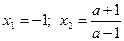

4) а=– 2, _.

Пример 7. При каких значениях р корни уравнения х ²+6 х + р +3=0 будут отрицательными?

1. Квадратное уравнение имеет действительные корни при условии D³ 0.

Найдем дискриминант этого уравнения и найдем значения параметра, удовлетворяющие этому условию

D= 36–4(p +3)=36–4 p –12=24–4 p

24–4 p ³0 Û p £6

2. При p £6 корни квадратного уравнения вычисляются по формулам

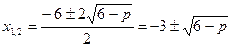
3. Найдем значения р, для которых х ₁<0 и x ₂<0, то есть решим систему

второе неравенство системы выполняется при любом p £6.

Решим первое неравенство системы

0£ <3 (так как арифметический корень – число неотрицательное).

0£6– р <9 Û –3< р £6.

4. Ответ: при –3< р £6 корни уравнения будут отрицательными.

Date: 2015-08-15; view: 700; Нарушение авторских прав