I. Линейные уравнения с параметром и уравнения, приводимые к линейным

В таких уравнениях «контрольными» значениями параметров, как правило, являются значения, обращающие в нуль коэффициенты при х.

Пример 1. Решить уравнение с параметром: 2 а (а –2) х=а– 2

1. «Контрольными» значениями являются значения, удовлетворяющие условию:

2 а (а –2)=0

решим это уравнение относительно переменной а.

2 а= 0 или а –2 = 0, откуда а= 0, а= 2.

2. Решим первоначальное уравнение при «контрольных» значениях параметра.

При а= 0 имеем 0× х=– 2, но это не имеет место ни при каких действительных значениях х, то есть в этом случае уравнение корней не имеет.

При а= 2 имеем 0× х= 0, это справедливо при любом значении х, значит, корнем уравнения является любое действительное число х.

3. Решим первоначальное уравнение, в случае, когда а¹ 0 и а¹ 2, тогда 2 а (а –2) ¹ 0 и обе части уравнения можно поделить на 2 а (а –2), получим:

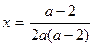, так как а¹ 2, то дробь можно сократить на (а –2), тогда имеем .

Ответ: при а= 0, корней нет;

при а= 2, корень – любое действительное число;

при а¹ 0, а¹ 2, .

Можно представить алгоритм решения такого типа уравнений.

1. Определить «контрольные» значения параметра.

2. Решить уравнение относительно х, при контрольных значениях параметра.

3. Решить уравнение относительно х, при значениях, отличных от «контрольных».

4. Записать ответ в виде:

Ответ: 1) при значениях параметра..., уравнение имеет корни...;

2) при значениях параметра..., уравнение имеет корни...;

3) при значениях параметра..., уравнение корней не имеет.

Пример 2. Решить уравнение с параметром

(а ²–2 а +1) х=а ²+2 а– 3

1. Найдем контрольные значения параметра

а ²–2 а +1=0 Û (а –1)²=0 Û а =1

2. Решим уравнение при а= 1

0× х= (1+2×1–3) Û 0× х= 0 Þ х – любое действительное число.

3. Решим уравнение при а¹ 1

а ²–2 а +1 ¹ 0 Þ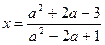

разложим числитель и знаменатель дроби на множители

так как а¹ 1, дробь можно сократить

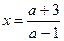
4. Ответ: 1) при а= 1, х – любое действительное;

2) при а¹ 1, .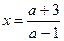

Пример 3. Решить уравнение с параметром

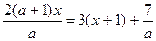
1. Так как параметр а стоит в знаменателе, то а обязательно должно быть отлично от нуля. При а¹ 0 приведем это уравнение к стандартному виду линейного уравнения, для чего обе части умножим на а.

2(а +1) х= 3 а (х +1)+7

2 ах +2 х= 3 ах +3 а +7

2 ах +2 х –3 ах= 3 а +7

(2– а) х= 3 а +7

найдем «контрольные» значения а

2– а= 0 Û а= 2

2. Решим уравнение при а= 2

0× х= 13

это равенство не имеет места ни при каких значениях х.

3. Решим уравнение при а¹ 2

2 –а¹ 0 Þ .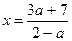

4. Ответ: 1) при а= 2, корней нет;

2) при а¹ 0, а¹ 2, ;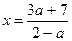

3) при а= 0 уравнение не имеет смысла.

Пример 4. Решить уравнение с параметром

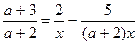
1. Так как параметр а стоит в знаменателе дроби, то чтобы уравнение имело смысл, а+ 2 обязательно должно быть отлично от нуля

а +2 ¹ 0 Û а¹– 2

так как х стоит в знаменателе дроби, то х¹ 0. Преобразуем уравнение

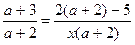
так как х¹ 0 и а¹– 2, уравнение равносильно уравнению

(а +3) х= 2 а –1

найдем контрольные значения параметра

а +3 = 0 Þ а=– 3.

2. Решим уравнение при а=– 3.

0× х=– 7

при любом х равенство места не имеет

3. Решим уравнение при а¹– 3, а+ 3 ¹ 0.

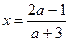
так как х¹ 0, то проверим, нет ли значений а, при которых х= 0, для этого приравняем полученную дробь к нулю

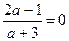Û ,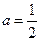

поэтому, чтобы уравнение имело смысл .

4. Ответ: 1) при а=– 3, а=– 2, 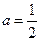, корней нет;

2) при а¹– 2, а¹– 3, , .

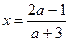Date: 2015-08-15; view: 657; Нарушение авторских прав