Общее определение тензоров

Векторы, ковекторы, линейные операторы, и билинейные формы - примеры тензоров. Они являются геометрическими объектами, которые представляются в числовой форме, после того, как выбран базис в пространстве. Это числовое представление является своим для каждого из них: векторы и ковекторы представляются одномерными массивами, линейные операторы и квадратичные формы - двумерными массивами. Кроме количества индексов, имеет значение также и их расположение. Координаты вектора нумеруются одним верхним индексом, который называется контравариантным индексом. Координаты ковектора нумеруются одним нижним индексом, который называется ковариантным индексом. В матрице билинейной формы мы используем два нижних индекса; поэтому билинейные формы называют дважды-ковариантными тензорами. Линейные операторы - тензоры смешанного типа; их элементы нумеруются одним нижним и одним верхним индексами. Число индексов и их положения определяют правила преобразования, т.е. то как компоненты каждого конкретного тензора ведут себя при смене базиса. В общем случае, любой тензор представляет собой многомерный массив с определенным числом верхних и нижних индексов. Давайте обозначать число этих индексов через r и s. Тогда получится тензор типа (r, s); или иногда используется термин валентность. Тензор типа (r, s), или тензор валентности (r, s) - это r-раз контравариантный и s-раз ковариантный тензор.

Все это была терминология; теперь давайте перейдем к точному определению.

Оно базируется на следующих общих формулах преобразования:

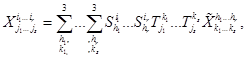(3.1)

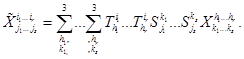(3.2)

Определение 1. Геометрический объект X, который в каждом базисе представляется (r + s)-мерным массивом 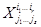вещественных чисел, удовлетворяющих правилам преобразования (3.1) и (3.2) при смене базиса, называется тензором типа (r, s), или валентности (r, s).

Индексы 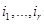и - свободные индексы. В правой стороне равенства (3.1) они распределены в S -ках и T -шках, каждый имеет только одно вхождение и сохраняет свою позицию при переходе из левой в правую часть равенства, т.е. верхние индексы 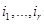остаются верхними, а нижние индексы остаются нижними в правой части равенства (3.1).

Остальные индексы 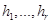и 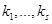- это индексы суммирования, они входят в правую часть (3.1) парами: один раз в качестве верхнего индекса и один раз в качестве нижнего индекса, один раз в S -матрице либо в T -матрице и второй раз среди индексов в компонентах массива .

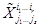При выражении 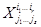через 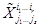каждый верхний индекс обслуживается ровно один раз матрицей прямого перехода S, порождая при этом ровно одно суммирование в формуле (3.1):

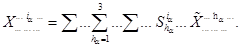(3.3)

Подобным же образом, каждый нижний индекс обслуживается матрицей обратного перехода T и тоже порождает одно суммирование в формуле (1):

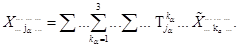(3.4)

Формулы (3.3) и (3.4) совпадают с (3.1), они записаны для того, чтобы сделать более понятным то, как записывается формула (3.1). Итак, определение тензоров дано.

Date: 2015-07-25; view: 468; Нарушение авторских прав