
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Линейные преобразования
|
|
Пусть переменные 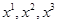 преобразуются в новые
преобразуются в новые 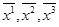 с помощью линейного преобразования
с помощью линейного преобразования
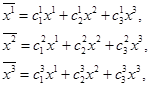
где 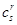 - константы (все индексы пробегают значения 1, 2, 3..., n независимо друг от друга.). Применяя условие о суммировании, можем записать эту систему уравнений в виде
- константы (все индексы пробегают значения 1, 2, 3..., n независимо друг от друга.). Применяя условие о суммировании, можем записать эту систему уравнений в виде
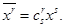 (1.1)
(1.1)
Мы предполагаем, что определитель преобразования 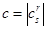 не равен нулю. Пусть
не равен нулю. Пусть 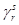 является алгебраическим дополнением элемента
является алгебраическим дополнением элемента 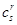 в определителе c деленным на величину
в определителе c деленным на величину 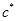 (
(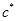 - обратная матрица). Тогда
- обратная матрица). Тогда
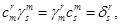 (1.2)
(1.2)
и мы можем разрешить систему уравнений (1.1) относительно x
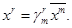 (1.3)
(1.3)
Это показывает, что данное преобразование обратимо.
Кроме того, если 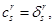 мы имеем
мы имеем
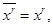
т. е. тождественное преобразование.
Если перейти сначала от переменных 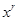 к
к 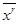 по (1.1), а затем от переменных
по (1.1), а затем от переменных 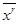 к
к 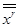 при помощи преобразования
при помощи преобразования
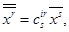
то мы видим, что переход от первоначальных переменных 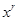 к
к 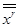 определяется формулой
определяется формулой
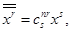
где
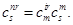
Это преобразование, следовательно, также линейное.
Говорят, что совокупность преобразований образует группу, когда она удовлетворяет следующим условиям: 1) если преобразования от 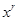 к
к 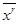 и от
и от 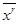 к
к 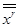 принадлежат данной совокупности, то преобразование от
принадлежат данной совокупности, то преобразование от 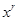 к
к 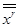 также принадлежат к ней; 2) совокупность преобразования содержит тождественное и обратное преобразования.
также принадлежат к ней; 2) совокупность преобразования содержит тождественное и обратное преобразования.
Таким образом, совокупность линейных преобразований образует группу.
Date: 2015-07-25; view: 407; Нарушение авторских прав