Надежность систем, работающих до первого отказа (показатели, методы расчета)

Под словом «элемент» мы будем понимать не только нераз­ложимую часть системы, но и любое устройство, надежность которого изучается независимо от надежности составляющих его частей.

Пусть в момент t=0 элемент начинает работу, а в момент t = τ происходит отказ. Будем говорить, что τ -время жизни элемента, Предположим, что τ -случайная величина с законом распределения

Q(t) = P{ τ <t}.

Функция Q(t) есть вероятность отказа элемента до момента t. Мы будем предполагать, что функция Q(t) непрерывна и существует непрерывная плотность вероятности отказа

q(t)=Q’(t)

Так, например, разрыв функции Q(t) означает, что в какой-то наперед заданный момент элемент может отказать с конечной вероятностью, что вряд ли может быть на практике. Исключение составляет лишь начальный момент t = 0, так как некоторые элементы отказывают в момент включения

Итак, мы предположили, что время жизни элемента τ есть случайная величина с законом распределения Q(t). Эта функция полностью определяет надежность нашего элемента. Наряду с ней и не менее часто употребляется и другая функция

P(t) = 1 – Q(t) = P{τ>t}

т. е. вероятность безотказной работы элемента за время t. Будем называть эту функцию так, как ее чаще всего называют, а именно, функцией надежности. функция n(t), которая равна числу элементов, не отказавших к моменту t. В начальный момент эта функция равна n(0) = N, а в момент каждого отказа она уменьшается на единицу. Отношение P_N(t) = 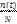называется эмпирической функцией надежности. Для больших N имеет место приближенное равенство:

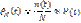
во многих случаях надежность характеризуют не функцией Р(t), а некоторыми числовыми величинами. Важнейшей из них является среднее время безотказной работы, которое определяется как математическое ожидание случайной величины τ.

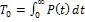
Другой характеристикой надежности является дисперсия времени жизни. Она может быть найдена из опыта, если испытывается N элементов τ_N, то при большом N

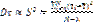, где

.

Величина 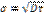дает нам среднеквадратическое уклонение случайного времени τ от своего среднего времени T₀.

Интенсивность отказа.

Пусть элемент проработал безотказно до момента t. Какова вероятность того, что он не откажет на участке (t, t₁) Обозначим эту вероятность через P(t, t₁). Пусть А - событие, означающее безотказную работу элемента на (0, t), а В- событие, означающее безотказную работу на (t, t₁). Тогда наша вероятность есть условная вероятность

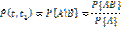
Но событие AB означает безотказную работу элемента на (0,t₁), поэтому

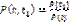Вероятность отказавыражается так

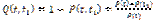
Положим теперь t₁=t+∆t и устремим ∆t к 0. Тогда

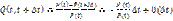Введем обозначение 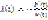. При малом дельта t 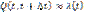. является локальной характеристикой надежности, определяющий надежность элемента в каждый данный момент времени. Говоря "по-инженерному", λ (t) есть вероятность того, что элемент, проработавший безотказно до момента t, откажет в последующую единицу времени (если, конечно, эта единица мала).

Date: 2015-07-25; view: 1024; Нарушение авторских прав