Метод пространства состояний

5.1.1.Постановка задачи

Имеются объекты, являющиеся системой, которая состоит из некоторого количества элементов. Каждый элемент может находиться в нескольких состояниях. Количество состояний каждого элемента конечно. Состояние системы определяется состоянием каждого элемента системы. Если изменяется состояние одного из элементов, то система переходит в новое состояние. Все возможные состояния системы образуют пространство состояний. Необходимо определить вероятности нахождения системы в том или ином состоянии с помощью метода пространства состояний.

5.1.2. Математическая модель надежности системы

При использовании метода пространства состояний в общем случае для системы S необходимо иметь математическую модель в виде множества состояний, в которых она может находиться.

Основные правила составления модели:

1. Математическую модель изображают в виде диаграммы пространства состояний или графа состояний (рис. 5.1).

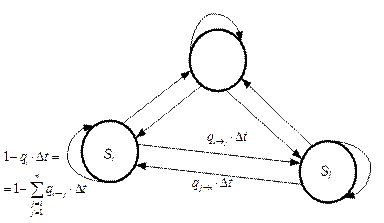
Рис. 5.1. Диаграмма (граф) пространства состояний

Элементами диаграммы пространства состояний являются кружки (вершины графа S ₁, S ₂, …, S _n) и стрелки. Кружки – возможные состояния системы S, а стрелки – возможные направления переходов из одного состояния S_i в другое S_j. Стрелки являются событиями.

Над или под стрелками указываются вероятности переходов из одного состояния в другое.

Петлёй обозначаются задержки в том или ином состоянии.

Диаграмма пространства состояний отображает конечное (дискретное) число возможных состояний системы.

2. Для описания случайного процесса перехода из состояния в состояние применяются вероятности состояний (см. п. 1.2) P ₁(t), P ₂(t), …, P _n(t). P _i(t) = P (S (t) = S_i) – вероятность нахождения системы в момент времени t в i -м состоянии.

Для любого времени t выполняется условие нормировки:

.

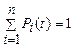(5.1)

3. По диаграмме пространства состояний составляется система обыкновенных дифференциальных уравнений первого порядка (система уравнений Чемпена – Колмогорова):

.

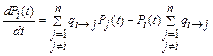(5.2)

Интенсивности переходов q_j®i и q_i®j должны быть постоянными величинами, т. е. независимыми от времени. Это возможно, когда все случайные величины, используемые в математической модели, распределены по экспоненциальному закону.

При составлении дифференциальных уравнений пользуются простейшим мнемоническим правилом:

- в левой части записываются производные по времени t от вероятности нахождения системы в каждом из возможных состояний ();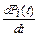

- число членов в правой части равно числу стрелок, соединяющих рассматриваемое состояние с другими состояниями;

- каждый член правой части равен произведению интенсивности перехода на вероятность того состояния, из которого выходит стрелка;

- знак произведения положителен, если стрелка входит в рассматриваемое состояние, и отрицателен, если стрелка выходит.

Проверкой правильности составления уравнений является равенство нулю суммы правых частей уравнений.

4 Чтобы решить систему дифференциальных уравнений для вероятностей состояний P ₁(t), P ₂(t), …, P _n(t), необходимо задать начальное значение вероятностей P ₁(0), P ₂(0), …, P _n(0) при t = 0, сумма которых равна 1, .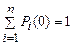

Если в начальный момент t = 0 состояние системы известно, например система S находится в i -м состоянии и P_i (0) = 1, то вероятности нахождения системы в любом другом состоянии равны 0.

Во многих приложениях интерес представляют только асимптотические значения вероятностей, в которых время наблюдения за системой стремится к бесконечности: P (t →¥). При возрастании периода наблюдения изменение P_i(t) уменьшается и при t →¥:

.

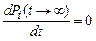(5.3)

Тогда уравнение Чемпена – Колмогорова представляется в виде

.

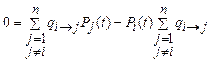(5.4)

Пример составления системы уравнений Чемпена – Колмогорова с тремя возможными состояниями системы.

В начале составляем диаграмму пространства состояний (рис. 5.2):

Рис. 5.2. Диаграмма пространства состояний для системы с тремя состояниями

На основании диаграммы пространства состояний записываем систему уравнений Чемпена – Колмогорова:

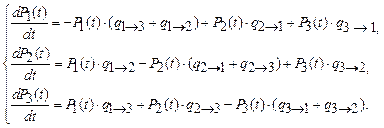
Так как из любых двух уравнений системы можно вывести третье, то при трех неизвестных имеем два независимых уравнения. Следовательно, чтобы решить систему, нужно составить еще одно независимое уравнение. Им является условие нормировки: .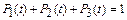

5.1.3. Связь частоты возникновения и продолжительности состояния с вероятностью нахождения системы в i-м состоянии и интенсивностью переходов для стационарных процессов

Частота появления i -го состояния W _i определяется как ожидаемое число пребываний системы в состоянии S_i в единицу времени при достаточно длительном наблюдении.

Чтобы связать частоту W _i, вероятность P_i и среднюю продолжительность данного состояния системы 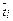, рассмотрим процесс функционирования системы, как состоящий из двух чередующихся интервалов времени – пребывание в состоянии S_i и пребывание вне этого состояния. Таким образом, система описывается процессом с двумя состояниями. Диаграмма пространства состояний для этого случая показана на рис 5.3.

Обозначим 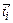как среднюю продолжительность пребывания вне состояния S_i.

Среднее время цикла в этом случае равно

.

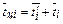(5.5)

Тогда

.

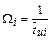(5.6)

Рис. 5.3. Процесс работы системы с двумя состояниями: «в состоянии i» и «вне состояния i»

Если умножить уравнение (5.6) на 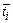, то правая часть примет вид 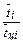, который соответствует геометрическому определению вероятности P_i. Тогда

.

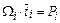(5.7)

Уравнение (5.7) дает связь между рассмотренными в этом разделе тремя параметрами.

Теперь свяжем частоту W _i, среднюю продолжительность данного состояния системы 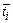и интенсивность переходов системы. Для этого введем понятие частоты перехода из состояния i в состояние j. Эта частота (W _i®j) определяется как ожидаемое число переходов из состояния i непосредственно в состояние j в единицу времени. Следовательно,

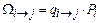
(5.8)

(подробный вывод формулы приведен в [3]).

Из определения W _i и W _i®j следует, что

.

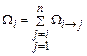(5.9)

Подставляя в это выражение уравнение (5.8), получаем

.

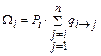(5.10)

Наконец, объединяя (5.7) и (5.10), получаем выражение для :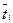

.

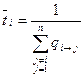(5.11)

При помощи уравнений (5.4), (5.10), (5.11) и условия нормировки можно вычислить все характеристики состояний, исходя из интенсивности переходов, определяющих данную систему.

В заключение данного раздела приведем алгоритм определения вероятностей нахождения объекта в каждом из возможных состояний в любой момент времени (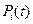) (при этом продолжительности каждого состояния распределены по экспоненциальному закону):

1. Составляется диаграмму пространства состояний по временной диаграмме состояний с неизвестными параметрами .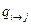

Date: 2015-07-25; view: 665; Нарушение авторских прав