Задачи для самоподготовки. Задача №1. Временная диаграмма состояний системы, которая может находиться в пяти состояниях, представлена на рис

Задача №1. Временная диаграмма состояний системы, которая может находиться в пяти состояниях, представлена на рис. 5.19.

Известно следующее:

- продолжительность пребывания системы в каждом из состояний подчинены экспоненциальному закону;

- средняя продолжительность пребывания системы в каждом из состояний:

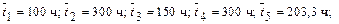
- S ₂È S ₃ = S ₆ – рабочее состояние; S ₁È S ₄ = S ₇ – состояние аварийного ремонта; S ₅ – состояние планово-предупредительного ремонта.

Рис. 5.19. Временная диаграмма состояний системы

Задание:

1. Составить диаграмму пространства состояний по данной временной диаграмме состояний системы.

Определить:

- частоту появления каждого из состояний (W₁, W₂, W₃, W₄, W₅ – 1/год);

- вероятности нахождения системы в каждом из пяти состояний в стационарном режиме работы (P ₁(¥), P ₂(¥), P ₃(¥), P ₄(¥), P ₅(¥));

- интенсивности переходов из состояния в состояние (q _1®2, q _1®3, q _3®2, q _4®5 и т. д. – 1/год).

2. Составить диаграмму пространства состояний для данной системы, которая имеет три состояния: S ₅, S ₆, S ₇. Определить с помощью этой диаграммы вероятности нахождения системы в работоспособном состоянии, состоянии аварийного ремонта и в состоянии планово-предупредительного ремонта для установившегося (стационарного) процесса.

Задача №2. Временная диаграмма состояний системы, которая может находиться в пяти состояниях, представлена на рис. 5.20.

Известно следующее:

- продолжительность пребывания системы в каждом из состояний подчинена экспоненциальному закону;

- средняя продолжительность пребывания системы в каждом из состояний:

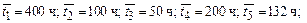
- S ₁È S ₂ = S ₆ – рабочее состояние; S ₃È S ₅ = S ₇ – состояние аварийного ремонта; S ₄ – состояние планово-предупредительного ремонта.

Рис. 5.20. Временная диаграмма состояний системы

Задание:

1. Составить диаграмму пространства состояний по данной временной диаграмме состояний системы.

Определить:

- частоту появления каждого из состояний (W₁, W₂, W₃, W₄, W₅ – 1/год);

- вероятности нахождения системы в каждом из пяти состояний в стационарном режиме работы (P ₁(¥), P ₂(¥), P ₃(¥), P ₄(¥), P ₅(¥));

- интенсивности переходов из состояния в состояние (q _1®2, q _1®3, q _3®2, q _4®5 и т. д. – 1/год).

2. Составить диаграмму пространства состояний для данной системы, которая имеет три состояния: S ₆, S ₇, S ₄. Определить с помощью этой диаграммы вероятности нахождения системы в работоспособном состоянии, состоянии аварийного ремонта и в состоянии планово-предупредительного ремонта для установившегося (стационарного) процесса.

Задача №3. Диаграмма пространства состояний системы представлена на рис. 5.21.

Известно следующее:

- продолжительность пребывания системы в каждом из состояний подчинена экспоненциальному закону;

- все интенсивности переходов из состояния в состояние имеют одинаковые значения:

q _1®2 = q _1®3 = q _1®4 = q _1®5 = q _2®1 = q _2®3 = q _2®4 = q _2®5 = q _3®1 = q _3®2 = q _3®4 = q _3®5 = q _4®1 = q _4®2 = q _4®3 = q _4®5 = q _5®1 = q _5®2 = q _5®3 = = q _5®4 = 2,5 год^-1;

- S ₁È S ₂ = S ₆ – работоспособное состояние; S ₃È S ₄È S ₅ = S ₇ – состояние аварийного ремонта;

- в начальный момент времени система находится в состоянии S ₃.

Задание:

Преобразовав исходную диаграмму пространства состояний в диаграмму с двумя состояниями, определить:

1) вероятность нахождения системы в работоспособном состоянии в момент времени t = 0,5 (года);

2) вероятность безотказной работы в момент времени t = 0,1 (года).

Задача №4. Диаграмма пространства состояний системы представлена на рис. 5.21.