
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Список использованных источников. 70
|
|
Введение. 4
Раздел I. Матрицы и определители. 5
§ 1.1. Матрицы, их виды.. 5
1.1.1. Виды матриц. 5
1.1.2. Задачи для самостоятельного решения. 7
§ 1.2. Действия над матрицами. 8
1.2.1. Сложение матриц. 8
1.2.2. Умножение матрицы на число. 8
1.2.3. Умножение матриц. 8
1.2.4. Свойства операций над матрицами. 10
§ 1.3. Определители 2, 3, n -го порядков. 13
§ 1.4. Основные свойства определителей. 16
§ 1.5. Миноры и алгебраические дополнения. Теорема разложения. 18
1.5.1. Теорема разложения. 18
§ 1.6. Обратная матрица. 20
1.6.1. План нахождения обратной матрицы.. 21
§ 1.7. Ранг матрицы.. 25
1.7.1. Методы вычисления ранга матрицы.. 25
Раздел II. Системы линейных алгебраических уравнений. 30
§ 2.1. Основные понятия и определения. 30
2.1.1.Эквивалентные преобразования систем линейных
алгебраических уравнений. 30
§ 2.2. Решение систем n линейных уравнений с n неизвестными
по формулам Крамера. 31
§ 2.3. Решение систем линейных уравнений матричным методом. 35
§ 2.4. Решение систем линейных уравнений методом Гаусса. 41
§ 2.5. Исследование систем линейных уравнений
по теореме Кронекера-Капелли. 51
Раздел III. Задания для выполнения расчетно-графической работы... 56
Раздел IV. Образец выполнения расчетно-графической работы... 68
Список использованных источников. 70
ВВЕДЕНИЕ
Математика проникла практически во все сферы человеческой деятельности. Это объясняется, во-первых, тем, что она способна создавать модели изучаемых явлений, а во-вторых — используется для обработки цифровых данных как средство расчета. В настоящее время различные численные и аналитические методы используются не только в естественных, но и в гуманитарных науках. С помощью математических методов можно более глубоко анализировать сложные экономические явления и процессы.
Как наука математика имеет определенное математическое мировоззрение, однако для специалистов в различных областях она является, прежде всего, мощным инструментарием при проведении необходимых расчетов и исследований, а также фундаментом, на котором строится современное знание высшего профессионального образования.
Широкое применение математики в самых различных областях науки и техники повышает требования к математической подготовке будущих специалистов. Преподавание математики в вузе ставит цель — ознакомить студентов с основами математического аппарата, необходимого для решения теоретических и практических задач, научить их самостоятельно изучать литературу по математике и ее приложениям.
В данном пособии рассматривается один из важнейших разделов высшей математики — «Линейная алгебра», который используется при решении различных задач, как математики, так и ее приложений.
Раздел I. МАТРИЦЫ И ОПРЕДЕЛИТЕЛИ
§ 1.1. Матрицы, их виды
Матрицей называется прямоугольная таблица, образованная из элементов некоторого множества, состоящая из m строк и n столбцов.
Матрица записывается в виде
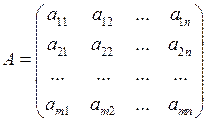 ,
,
где aij — элемент матрицы;
i = 1, 2, 3…, m — номер строки;
j = 1, 2, 3…, n — номер столбца.
Матрицу А называют матрицей размера m ´ n (или размерности m ´ n) и пишут Am´n.
Элементы, стоящие на диагонали, идущей из верхнего левого угла, образуют главную диагональ.
Наиболее часто рассматривают матрицы, элементами которых являются числа.
1.1.1. Виды матриц
1. Матрица, у которой число строк равно числу столбцов, т.е. m = n, называется квадратной матрицей n-го порядка. Например,
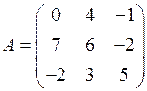 — квадратная матрица 3-го порядка.
— квадратная матрица 3-го порядка.
2. Квадратная матрица, у которой все элементы, кроме элементов главной диагонали, равны нулю, называются диагональной. При этом среди элементов, стоящих на главной диагонали, могут быть равные нулю. Например,
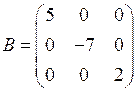 — диагональная матрица третьего порядка.
— диагональная матрица третьего порядка.
3. Диагональная матрица, у которой все элементы, стоящие на главной диагонали равны единице, называют единичной. Обозначается буквой Е. Например,
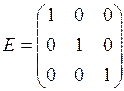 — единичная матрица 3-го порядка.
— единичная матрица 3-го порядка.
4. Квадратная матрица называется верхней (нижней) треугольной, если все элементы, расположенные ниже (выше) главной диагонали, равны нулю. Например,
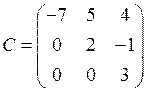 — верхняя треугольная матрица 3-го порядка;
— верхняя треугольная матрица 3-го порядка;
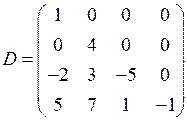
| — нижняя треугольная матрица 4-го порядка. |
5. Матрица, все элементы которой равны нулю, называется нулевой. Обозначается буквой О. Например,
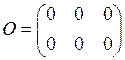 — нулевая матрица размерности
— нулевая матрица размерности 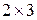 .
.
6. Матрица, содержащая один столбец (одну строку), называется матрицей-столбцом (матрицей-строкой). Например,
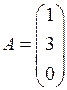 — матрица-столбец размерности
— матрица-столбец размерности 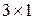 ;
;
В = (4; 2; 5; – 3) — матрица-строка размерности 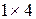 .
.
Две матрицы А и В одного размера называются равными, если равны все соответствующие элементы этих матриц, т.е. А = В, если aij = bij.
Матрица, полученная из данной, заменой каждой ее строки столбцом с тем же номером, называется транспонированной к данной. Обозначается АТ. Например, если
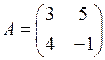 , то
, то 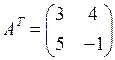 .
.
Задачи для самостоятельного решения
1.1. Дана матрица 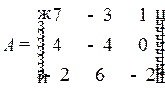 . Тогда сумма элементов, расположенных на главной диагонали этой матрицы, равна…
. Тогда сумма элементов, расположенных на главной диагонали этой матрицы, равна…
1) – 5 2) 1 3) 5 4) 9
1.2. Укажите соответствие между матрицей и ее типом
1) 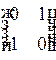 2)
2) 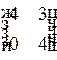 3)
3) 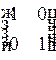 4)
4) 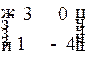
а) симметричная
б) единичная
с) нижняя треугольная
д) верхняя треугольная
1.3. Для матрицы 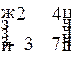 транспонированной матрицей будет матрица…
транспонированной матрицей будет матрица…
1) 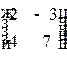 2)
2) 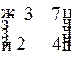 3)
3) 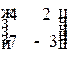 4)
4) 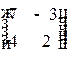
1.4. Матрица 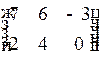 равна матрице…
равна матрице…
1) 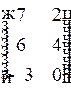 2)
2) 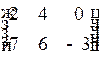 3)
3) 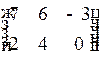 4)
4) 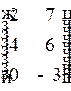
1.5. Укажите соответствие между матрицей и ее размерностью
1) 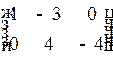 2)
2)  3)
3) 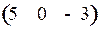 4)
4) 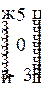
а) 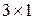 в)
в) 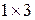 с)
с) 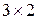 д)
д) 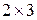
§ 1.2. Действия над матрицами
1.2.1. Сложение матриц
Суммой двух матриц А и В одинаковой размерности называется матрица С = А + В той же размерности, элементы которой равны сумме соответствующих элементов слагаемых матриц, т.е. 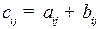 .
.
Пример 1.1. Вычислить сумму матриц А + В,
где 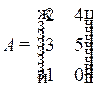 ,
, 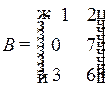 .
.
Решение
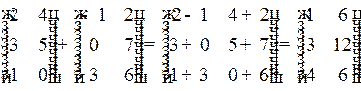 .
.
1.2.2. Умножение матрицы на число
Произведением матрицы А на число a называется матрица В = a А той же размерности, элементы которой получены умножением всех элементов матрицы А на число a, т.е. 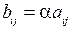 .
.
Пример 1.2. Вычислить 2 А, где 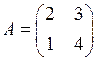 .
.
Решение
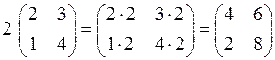 .
.
Следствие: Общий множитель всех элементов матрицы можно выносить за знак матрицы. Например,
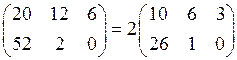 .
.
1.2.3. Умножение матриц
Произведение матриц 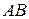 можно вычислить только, если число столбцов первой матрицы А равно числу строк второй матрицы В. В результате получим матрицу С, у которой столько же строк, как и у матрицы А, и столько же столбцов, как и у матрицы В. При этом каждый элемент сij матрицы С равен сумме произведений элементов i -ой строки матрицы А на соответствующие элементы j -го столбца матрицы В, т.е.
можно вычислить только, если число столбцов первой матрицы А равно числу строк второй матрицы В. В результате получим матрицу С, у которой столько же строк, как и у матрицы А, и столько же столбцов, как и у матрицы В. При этом каждый элемент сij матрицы С равен сумме произведений элементов i -ой строки матрицы А на соответствующие элементы j -го столбца матрицы В, т.е.
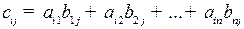 , где i = 1, 2, …, m; j = 1,2, …, p.
, где i = 1, 2, …, m; j = 1,2, …, p.
Схема умножения матриц представлена на рис. 1.

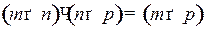

Рис. 1
Пример 1.3. Даны матрицы 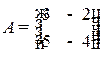 ,
, 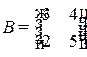 .
.
Найдите 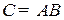 .
.
Решение
Найдем размерность матрицы-произведения С:
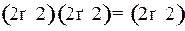 .
.
Вычислим элементы матрицы С:
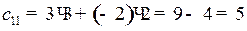 (сумма произведений элементов 1-й строки матрицы А на соответствующие элементы 1-го столбца матрицы В);
(сумма произведений элементов 1-й строки матрицы А на соответствующие элементы 1-го столбца матрицы В);
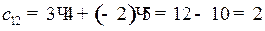 (сумма произведений элементов 1-й строки матрицы А на соответствующие элементы 2-го столбца матрицы В);
(сумма произведений элементов 1-й строки матрицы А на соответствующие элементы 2-го столбца матрицы В);
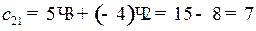 (сумма произведений элементов 2‑й строки матрицы А на соответствующие элементы 1-го столбца матрицы В);
(сумма произведений элементов 2‑й строки матрицы А на соответствующие элементы 1-го столбца матрицы В);
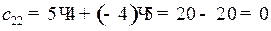 (сумма произведений элементов 2‑й строки матрицы А на соответствующие элементы 2-го столбца матрицы В).
(сумма произведений элементов 2‑й строки матрицы А на соответствующие элементы 2-го столбца матрицы В).
Тогда 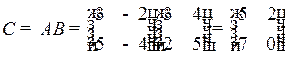 .
.
1.2.4. Свойства операций над матрицами
1. А + В = В + А;
2. А + (В + С) = (А + В) + С;
3. А + О = А;
4. А + (– А) = О;
5. 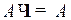 ;
;
6. 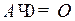 ;
;
7. 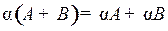 ;
;
8. 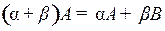 ;
;
9. 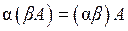 ;
;
10. 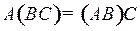 ;
;
11. 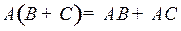 ;
;
12. 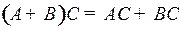 ;
;
13. 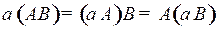 ;
;
14. 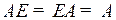 ,
,
где А, В, С, Е, О — матрицы, a, b — числа.
Переместительный закон умножения для матриц, в общем случае, не выполняется, т.е. АВ ¹ ВА.
Пример 1.4. Выполните указанные действия:
1) 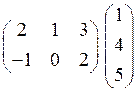 2)
2) 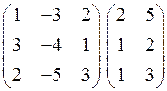 3)
3) 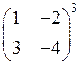
Решение
1) 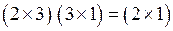 .
.
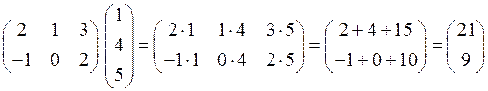 .
.
2) 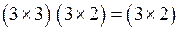 .
.
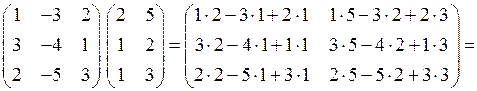
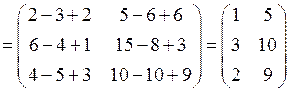 .
.
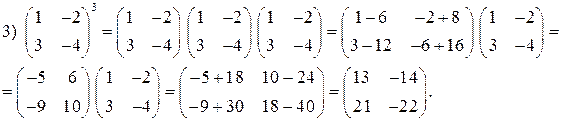
Задачи для самостоятельного решения
1.6. Даны матрицы 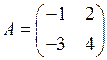 ,
, 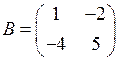 . Тогда разностью
. Тогда разностью 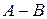 является матрица…
является матрица…
1) 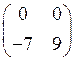 2)
2) 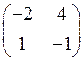 3)
3) 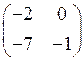 4)
4) 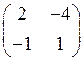
1.7. 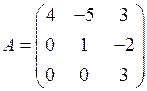 . Тогда матрица 4 А имеет вид…
. Тогда матрица 4 А имеет вид…
1) 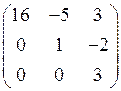 2)
2) 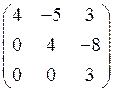 3)
3) 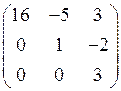
4) 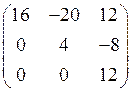 .
.
1.8. Произведением ВА матриц 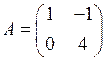 и
и 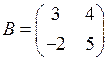 является матрица…
является матрица…
1) 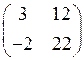 2)
2) 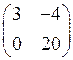 3)
3) 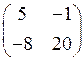 4)
4) 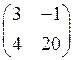
1.9. Размерность матрицы А — 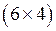 , а размерность матрицы В —
, а размерность матрицы В — 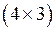 . Тогда произведение АВ имеет размерность…
. Тогда произведение АВ имеет размерность…
1) 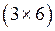 2)
2) 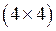 3)
3) 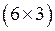 4)
4) 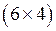 .
.
1.10. Даны матрицы  ,
, 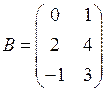 ,
, 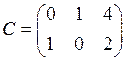 .
.
Укажите, в каком случае умножение матриц не определено.
1) СА 2) АВ 3) АА 4) ВА 5) ВС
1.11. Размерность матрицы А — 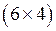 , а размерность матрицы В —
, а размерность матрицы В — 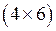 . Тогда сумма А + В …
. Тогда сумма А + В …
1) имеет размерность 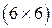
2) не определена
3) имеет размерность 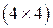
4) имеет размерность 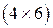
5) имеет размерность 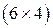
1.12. 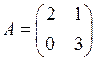 . Тогда матрица
. Тогда матрица 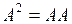 имеет вид…
имеет вид…
1) 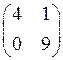 2)
2) 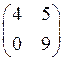 3)
3) 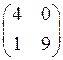 4)
4) 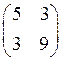
Выполните нижеуказанные действия.
1.13. 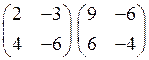 .
.
1.14. 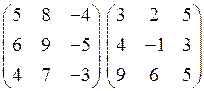 .
.
1.15. 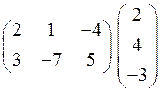 .
.
1.16. 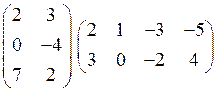
1.17. 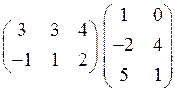 .
.
1.18. Найдите матрицу 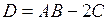 , где
, где
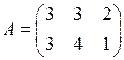 ,
,  ,
, 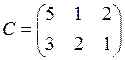 .
.
1.19. Дано матричное уравнение
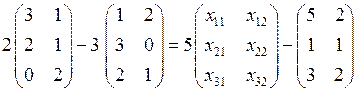 .
.
Найдите матрицу неизвестных.
1.20. Проверьте, выполняется ли равенство (А + В)2 = А 2 + 2 АВ + В 2, если 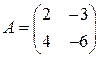 ,
, 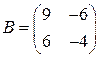 .
.
§ 1.3. Определители 2, 3, n-го порядков
Определителем 2-го порядка, соответствующим квадратной матрице 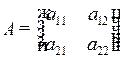 2-го порядка, называется число, равное
2-го порядка, называется число, равное 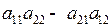 и обозначаемое
и обозначаемое 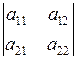 .
.
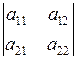 =
= 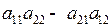 .
.
Определитель матрицы А обозначается D А, или 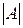 , или detA и читается соответственно дельта А, или определитель матрицы А, или детерминант матрицы А.
, или detA и читается соответственно дельта А, или определитель матрицы А, или детерминант матрицы А.
Элементы а 11, а 22 образуют главную диагональ определителя, а 12, а 21 — побочную. Схема вычисления определителя 2-го порядка представлена на рис. 2.

Рис. 2
Пример 1.5. Вычислить определитель 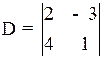 .
.
Решение
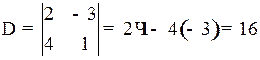 .
.
Ответ: 16.
Пример 1.6. Вычислить определитель 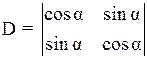 .
.
Решение
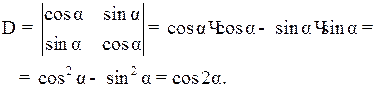
Ответ: cos2a.
Определителем 3-го порядка, соответствующим квадратной матрице
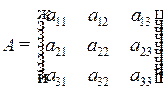 3-го порядка, называется число, равное
3-го порядка, называется число, равное
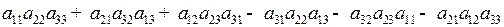 ,
,
и обозначаемое
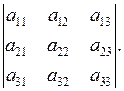
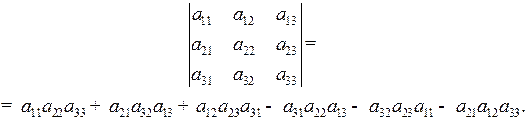
Схема вычисления определителя 3-го порядка по правилу треугольников (правилу Саррюса) представлена на рис. 3.

Рис. 3
Пример 1.7. Вычислить определитель 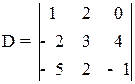 .
.
Решение
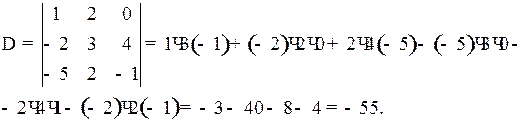
Ответ: – 55.
Пример 1.8.Найдите, при каком значении n определитель
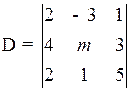 равен нулю.
равен нулю.
Решение
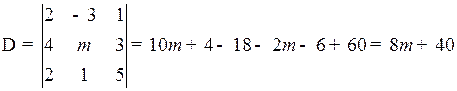 ;
;
D = 0, 8 m + 40 = 0, 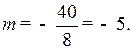
При m = – 5 определитель равен нулю.
Ответ: –5.
Определителем n -го порядка, соответствующим квадратной матрице размерности 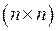 , называется число, найденное по определенному закону, представляющему из себя сумму n! слагаемых.
, называется число, найденное по определенному закону, представляющему из себя сумму n! слагаемых.
§ 1.4. Основные свойства определителей
1. Определитель не изменится, если его строки поменять местами с соответствующими столбцами. Это действие называется транспонированием.
Пусть 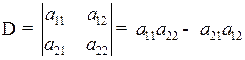 .
.
Транспонируем определитель D:
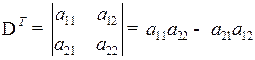 ;
;
D Т = D.
2. Если в определителе поменять местами какие-либо две строки (столбца), то определитель изменит знак на противоположный.
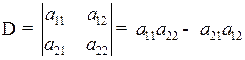 ;
;
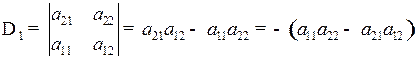 ;
;
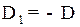 .
.
3. Общий множитель элементов какой-либо строки (столбца) определителя можно вынести за знак определителя.
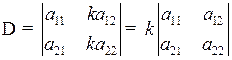 .
.
4. Если в определителе какая-либо строка (столбец) состоит из нулей, то определитель равен нулю.
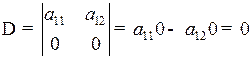 .
.
5. Если в определителе какие-либо две строки (столбца) пропорциональны, то определитель равен нулю.
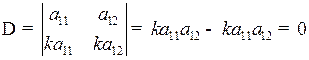 .
.
6. Если все элементы какой-либо строки (столбца) умножить на одно и тоже число и прибавить к соответствующим элементам другой строки (столбца), то определитель не изменится.
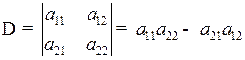 .
.
Элементы 1-й строки умножим на число k и прибавим к элементам 2-й строки:
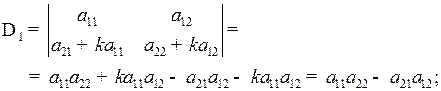
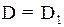 .
.
Пример 1.9. Вычислить определитель 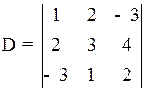
двумя способами:
1) по правилу треугольников;
2) упростив определитель по свойствам и затем применив правило треугольников.
Решение
1) По правилу треугольников:
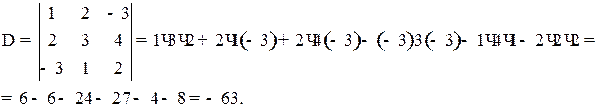
2) Используя свойство (6), умножим элементы 1-й строки на (–2) и прибавим к соответствующим элементам 2-й строки. Затем умножим элементы 1-й строки на 3 и прибавим к соответствующим элементам 3-й строки. Получим:
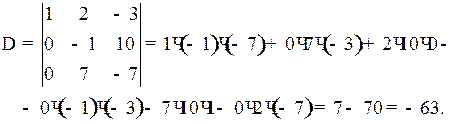
Ответ: – 63.
§ 1.5. Миноры и алгебраические дополнения.
Теорема разложения
Минором Mij. элемента aij определителя n -го порядка называется определитель (n – 1)-го порядка, который получается после вычеркивания i -й строки и j -го столбца, на пересечении которых стоит этот элемент.
Пусть, дан определитель 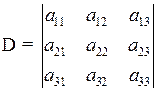 .
.
Минор элемента а 11 получается после вычеркивания 1-й строки и 1-го столбца определителя, т.е. 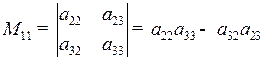 .
.
Минор элемента а 23 получается после вычеркивания 2-й строки и 3-го столбца определителя, т.е. 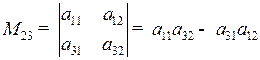 .
.
Алгебраическим дополнением Аij элемента aij определителя называется минор Mij, взятый со знаком (– 1) i + j .
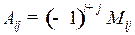 .
.
Например, в условиях предыдущего примера:
А 11 = (– 1)1+1 М 11 = М 11 = а 22 а 33 – а 32 а 23,
А 23 = (– 1)2+3 М 23 = – М 23 = – (а 11 а 32 – а 31 а 12) = а 31 а 12 – а 11 а 32.
1.5.1. Теорема разложения
Определитель равен сумме произведений элементов любой строки (столбца) на их алгебраические дополнения.
Пусть 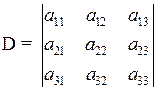 .
.
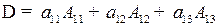 — разложение определителя по элементам первой строки;
— разложение определителя по элементам первой строки;
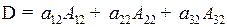 — разложение определителя по элементам второго столбца.
— разложение определителя по элементам второго столбца.
Пример 1.10. Вычислить определитель 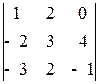 , разложив его по элементам первой строки.
, разложив его по элементам первой строки.
Решение
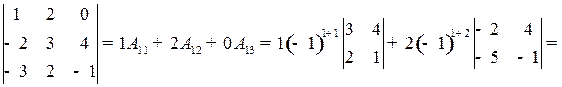
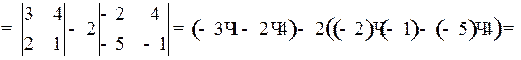
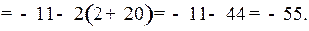
Ответ: – 55.
Замечание. Теорема разложения позволяет понизить порядок определителя на единицу.
Пример 1.11. Вычислить определитель 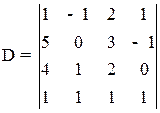 , используя свойство (6) и теорему разложения.
, используя свойство (6) и теорему разложения.
Решение
Элементы 1-й строки прибавим к соответствующим элементам 2-й строки. Потом элементы 1-й строки умножим на (–1) и прибавим к соответствующим элементам 4-й строки. Затем разложим определитель по элементам 4-го столбца. Получим:
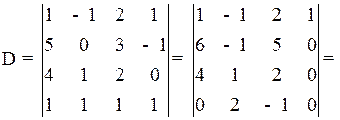
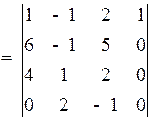
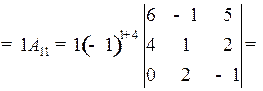
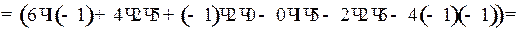
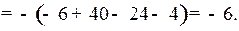
Ответ: – 6.
Задачи для самостоятельного решения
Вычислить определители:
1.21. 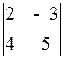 . 1.22.
. 1.22. 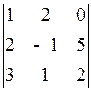 . 1.23.
. 1.23. 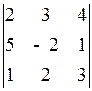 .
.
1.24. 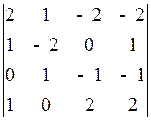 . 1.25.
. 1.25. 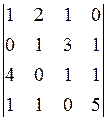 .
.
Решить уравнения:
1.26. 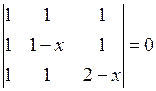 . 1.27.
. 1.27. 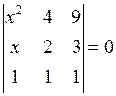 .
.
§ 1.6. Обратная матрица
Квадратная матрица А называется невырожденной, если ее определитель не равен нулю, и вырожденной, если ее определитель равен нулю.
Например, матрица 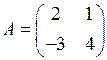 — невырожденная, так как ее определитель
— невырожденная, так как ее определитель 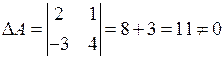 , а матрица
, а матрица 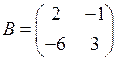 — вырожденная, так как ее определитель
— вырожденная, так как ее определитель  .
.
Матрица А –1 называется обратной к матрице А, если при умножении этой матрицы на данную как справа, так и слева получается единичная матрица:
АА –1 = А –1 А = Е.
Для того, чтобы квадратная матрица А имела обратную, необходимо и достаточно, чтобы она была невырожденной, т.е. D А ¹ 0.
1.6.1. План нахождения обратной матрицы
1. Находим D А — определитель матрицы А.
2. Находим алгебраические дополнения всех элементов матрицы А и составляем из них матрицу А *.
3. Транспонируем матрицу А * и получаем союзную матрицу 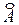 .
.
4. Находим обратную матрицу по формуле:
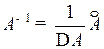 . (1.1)
. (1.1)
Проверить правильность нахождения обратной матрицы А –1 можно, исходя из определения, вычислив АА –1 или А –1 А. Должна получиться единичная матрица Е.
Пример 1.12. Найдите матрицу, обратную к матрице 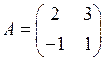 . Результат проверьте, вычислив произведение данной и полученной матриц.
. Результат проверьте, вычислив произведение данной и полученной матриц.
Решение
1. Найдем определитель матрицы А:
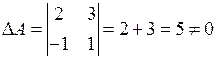 .
.
Следовательно, матрица А невырожденная, и для нее существует обратная матрица.
2. Найдем алгебраические дополнения всех элементов матрицы А:
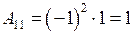 ,
, 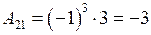 ,
,
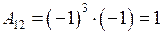 ,
, 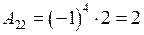 .
.
Составим матрицу А * из алгебраических дополнений элементов матрицы А:
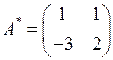 .
.
3. Транспонируем матрицу А* и получаем союзную матрицу 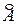 :
:
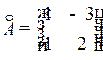 .
.
4) Находим обратную матрицу по формуле (1.1) 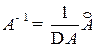 :
:
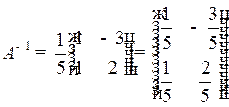 .
.
Проверка:
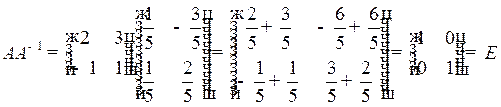 .
.
Следовательно, обратная матрица А– 1 найдена верно.
Пример 1.13. Найдите матрицу, обратную к матрице
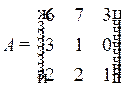 . Выполните проверку.
. Выполните проверку.
Решение
1. Найдем определитель матриц А:

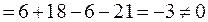 .
.
Следовательно, матрица А является невырожденной, и для нее существует обратная матрица.
2. Составим матрицу А * из алгебраических дополнений элементов матрицы А:
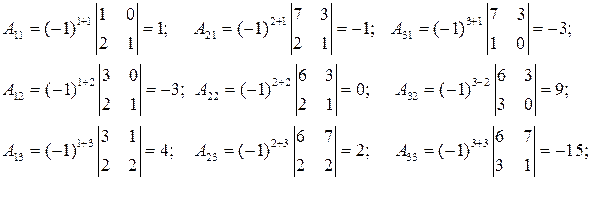
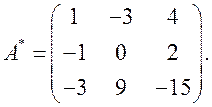
3. Транспонируем матрицу А *, получаем союзную матрицу 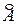 :
:
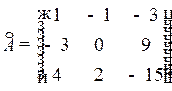 .
.
4. Найдем обратную матрицу А–1 по формуле (1.1) 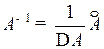 :
:
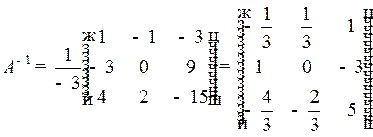 .
.
Проверка:
Найдем произведение А –1 А:
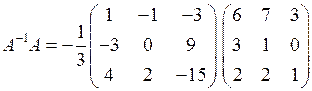 ;
;
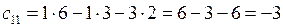 ,
,
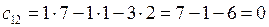 ,
,
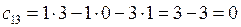 ,
,
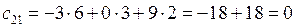 ,
,
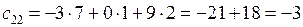 ,
,
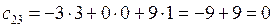 ,
,
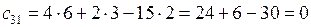 ,
,
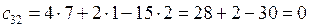 ,
,
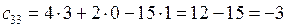 .
.
Тогда
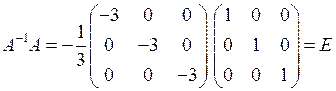 .
.
Следовательно, обратная матрица А –1 найдена верно.
Итак,
 .
.
Задачи для самостоятельного решения
1.28. Матрица 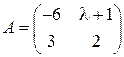 является вырожденной при l, равном…
является вырожденной при l, равном…
1) 3; 2) – 3; 3) 5; 4) другой ответ.
1.29. Матрица 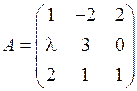 имеет обратную, если…
имеет обратную, если…
1)  ; 2)
; 2) 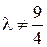 ; 3)
; 3) 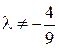 ; 4)
; 4) 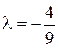 .
.
1.30. Выясните, для каких из приведенных ниже матриц имеются обратные:
1) 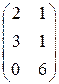 ; 2)
; 2) 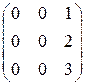 ; 3)
; 3) 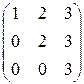 ; 4)
; 4) 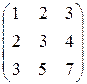 .
.
1.31. При каких значениях l матрица 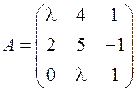 не имеет обратной?
не имеет обратной?
1.32. Найдите матрицу, обратную к матрице 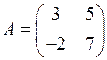 , и сделайте проверку.
, и сделайте проверку.
1.33. Найдите матрицу, обратную к матрице 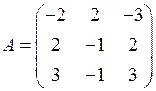 , и сделайте проверку.
, и сделайте проверку.
1.34. Покажите, что матрица 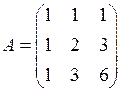 является обратной к матрице
является обратной к матрице 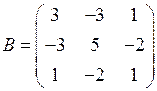 .
.
§ 1.7. Ранг матрицы
Рассмотрим матрицу размера 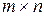 .
.
Рангом матрицы А называется наивысший порядок отличного от нуля минора этой матрицы.
Ранг матрицы А обозначается 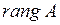 или
или 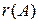 .
.
Из определения следует:
1) 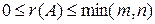 , где
, где 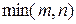 ― меньшее из чисел m и n;
― меньшее из чисел m и n;
2) 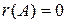 тогда и только тогда, когда все элементы матрицы равны нулю, т.е.
тогда и только тогда, когда все элементы матрицы равны нулю, т.е. 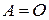 ;
;
3) для квадратной матрицы n -го порядка 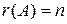 тогда и только тогда, когда матрица А невырожденная, т.е.
тогда и только тогда, когда матрица А невырожденная, т.е. 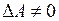 .
.
1.7.1. Методы вычисления ранга матрицы
1. Метод окаймления миноров
При вычислении ранга матрицы методом окаймления миноров следует переходить от миноров меньших порядков к минорам больших порядков. Если уже найден минор k -го порядка, отличный от нуля, то вычисляют лишь миноры (k + 1)-го порядка, окаймляющие минор k -го порядка. Если все они равны нулю, то ранг матрицы равен k.
Пример 1.14.Найти ранг матрицы 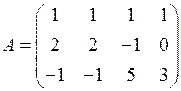 .
.
Решение
Так как матрица А имеет размер 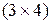 , то ее ранг
, то ее ранг
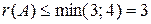 .
.
Минор 1-го порядка 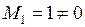 .
.
Окаймляем минор 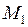 2-й строкой и 2-м столбцом, получаем минор 2-го порядка
2-й строкой и 2-м столбцом, получаем минор 2-го порядка
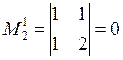 .
.
Окаймляем минор 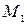 2-й строкой и 3-м столбцом. Для этого меняем 2-й и 3-й столбцы местами. Получаем минор 2-го порядка
2-й строкой и 3-м столбцом. Для этого меняем 2-й и 3-й столбцы местами. Получаем минор 2-го порядка
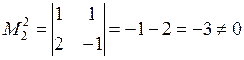 .
.
Вычисляем миноры 3-го порядка, окаймляющие минор второго порядка 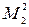 :
:
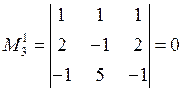 , так как имеет два одинаковых столбца;
, так как имеет два одинаковых столбца;
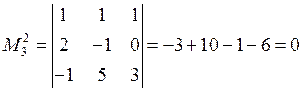 .
.
Так как все окаймляющие миноры 3-го порядка равны нулю, то 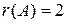 .
.
Ответ: 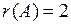 .
.
Примечание. В общем случае определение ранга матрицы методом окаймления миноров достаточно трудоемко.
2. Метод элементарных преобразований
К элементарным преобразованиям матриц относятся:
1) отбрасывание нулевой строки (столбца);
2) умножение всех элементов строки (столбца) на число, не равное нулю;
3) перемена местами строк (столбцов);
4) транспонирование;
5) прибавление к каждому элементу одной строки (столбца) соответствующих элементов другой строки (столбца), умноженных на одно и то же число.
Ранг матрицы не изменяется при ее элементарных преобразованиях.
Если одна матрица получается из другой с помощью конечного числа элементарных преобразований, то эти две матрицы называются эквивалентными.
Эквивалентные матрицы имеют одинаковые ранги.
С помощью элементарных преобразований матрицу можно привести к ступенчатому виду:
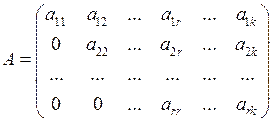 ,
,
где 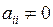 ; i = 1, 2, …, r;
; i = 1, 2, …, r; 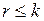 .
.
Ранг ступенчатой матрицы равен числу ее строк r, так как имеется минор r-го порядка, не равный нулю:
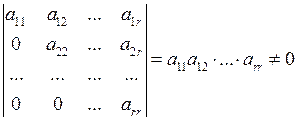 .
.
Алгоритм вычисления ранга матрицы с помощью элементарных преобразований рассмотрим на следующем примере.
Пример 1.8.Найти ранг матрицы 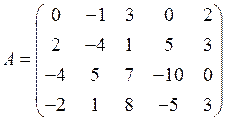 .
.
Решение
1. Если 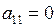 , то при перестановке строк или столбцов добиваемся того, что
, то при перестановке строк или столбцов добиваемся того, что 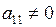 . Лучше, если
. Лучше, если 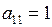 .
.
В данном примере умножим 2-й столбец на 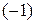 и поменяем его местами с 1-м:
и поменяем его местами с 1-м:
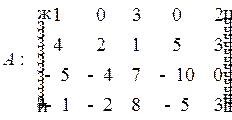 .
.
2. Если 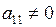 , то, умножая элементы 1-й строки на подходящие числа и прибавляя соответственно к ниже стоящим строкам, добиваемся того, чтобы все элементы 1-го столбца в них равнялись нулю.
, то, умножая элементы 1-й строки на подходящие числа и прибавляя соответственно к ниже стоящим строкам, добиваемся того, чтобы все элементы 1-го столбца в них равнялись нулю.
В данном примере умножим элементы 1-й строки на 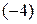 , затем на 5 и на 1 и прибавим соответственно ко 2-й, 3-й, 4-й строкам:
, затем на 5 и на 1 и прибавим соответственно ко 2-й, 3-й, 4-й строкам:
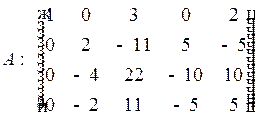 .
.
3. Если в полученной матрице 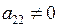 , то, умножая элементы 2-й строки на подходящие числа и прибавляя соответственно к ниже стоящим строкам, добиваемся того, чтобы все элементы 2-го столбца в них равнялись нулю.
, то, умножая элементы 2-й строки на подходящие числа и прибавляя соответственно к ниже стоящим строкам, добиваемся того, чтобы все элементы 2-го столбца в них равнялись нулю.
В данном примере умножим элементы 2-й строки на 2, затем на 1 и прибавим соответственно к 3-й и 4-й строкам:
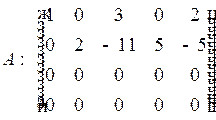 .
.
4. Если в процессе преобразований получаются нулевые строки (столбцы), то их вычеркиваем.
В данном примере вычеркиваем 3-ю и 4-ю нулевые строки:
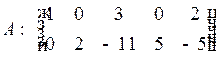 .
.
Получили матрицу ступенчатого вида. Ее ранг равен числу ненулевых строк, т.е. двум. Следовательно, и ранг данной матрицы 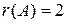 .
.
Ответ: 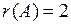 .
.
Задачи для самостоятельного решения
Вычислить ранги матриц:
1.35. 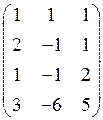 . 1.36.
. 1.36. 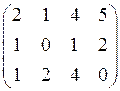 . 1.37.
. 1.37. 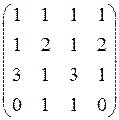 .
.
1.38. 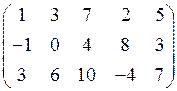 . 1.39.
. 1.39. 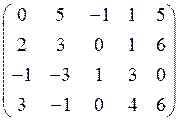 .
.
1.40. Найдите все значения параметра a, при которых ранг матрицы 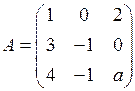 равен трем.
равен трем.
1.41. Найдите все значения параметра a, при которых ранг матрицы  равен двум.
равен двум.
Раздел II. СИСТЕМЫ ЛИНЕЙНЫХ
АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ
§ 2.1. Основные понятия и определения
Система m линейных алгебраических уравнений с n неизвестными имеет вид
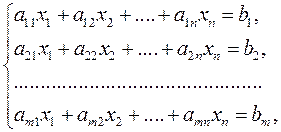
где аij — числовые коэффициенты при неизвестных,
i = 1, 2, …, m — номер уравнения,
j = 1, 2, …, n — номер неизвестной,
xj — неизвестные,
bi — свободные члены.
Решением системы называется совокупность чисел (с 1, с 2, …, сn), при подстановке которых вместо соответствующих неизвестных все уравнения системы обращаются в верные равенства.
Система уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет ни одного решения.
Совместная система линейных уравнений называется определенной, если она имеет одно решение, и неопределенной, если она имеет бесчисленное множество решений.
Если в системе все свободные члены bi равны нулю, то она называется однородной, а если хотя бы один из свободных членов bi не равен нулю, то она называется неоднородной.
Две системы с одним и тем же числом неизвестных называются равносильными (эквивалентными), если каждое решение одной из них является решением другой и наоборот.
2.1.1. Эквивалентные преобразования
систем линейных алгебраических уравнений
1. Перемена местами двух уравнений.
2. Умножение обеих частей какого-либо уравнения на действительное число, не равное нулю.
3. Прибавление к обеим частям одного уравнения системы соответствующих частей другого уравнения, умноженного на одно и то же действительное число.
4. Вычеркивание из системы уравнения вида 0 x 1 + 0 x 2 + …+ 0 xn = 0, так как ему удовлетворяют любые значения неизвестных.
Любое конечное число эквивалентных преобразований приводит исходную систему в ей равносильную.
§ 2.2. Решение систем n линейных уравнений
с n неизвестными по формулам Крамера
Рассмотрим систему трех линейных уравнений с тремя неизвестными
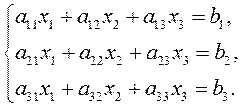
Определитель, составленный из коэффициентов при неизвестных, называется определителем системы (главным определителем системы):
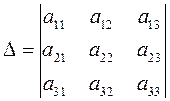 .
.
Обе части первого уравнения умножим на алгебраическое дополнение А 11 элемента а 11, обе части второго уравнения — на алгебраическое дополнение А 21 элемента а 21, обе части третьего уравнения — на алгебраическое дополнение А 31 элемента а 31 и сложим соответствующие части этих уравнений. Затем сгруппируем члены с х 1, с х 2 и с х 3 и вынесем их за скобки:
| (а 11 А 11 + а 21 А 21 + а 31 А 31) х 1 + (а 12 А 11 + а 22 А 21 + а 32 А 31) х 2 + + (а 13 А 11 + а 23 А 21 + а 33 А 31) х 3 = b 1 A 11 + b 2 A 21 + b 3 A 31. | (2.1) |
В равенстве (2.1) коэффициент при х 1 — это определитель системы D, разложенный по элементам первого столбца по теореме разложения.
Коэффициенты при х 2 и при х 3 равны нулю по теореме аннулирования (сумма произведений элементов любого столбца (строки) на алгебраические дополнения элементов другого столбца (строки) равна нулю).
В правой части стоит определитель, полученный из определителя D путем замены первого столбца (коэффициенты при х 1) столбцом свободных членов. Обозначим его через D x 1:
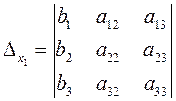 .
.
Тогда равенство (2.1) можно записать в виде 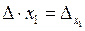 .
.
Если D ¹ 0, то
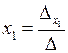 .
.
Аналогично можно найти х 2 и х 3:
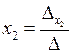 ,
, 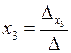 ,
,
где 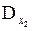 получен из определителя D путем замены второго столбца (коэффициенты при х 2) столбцом свободных членов, а
получен из определителя D путем замены второго столбца (коэффициенты при х 2) столбцом свободных членов, а 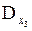 — заменой третьего столбца (коэффициенты при х 3) столбцом свободных членов.
— заменой третьего столбца (коэффициенты при х 3) столбцом свободных членов.
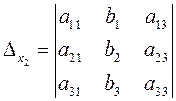 ,
, 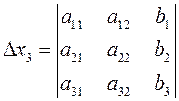 .
.
Итак, если определитель системы D ¹ 0, то решение системы можно найти по формулам:
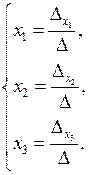
Эти формулы называются формулами Крамера.
Теорема Крамера. Если определитель системы n линейных алгебраических уравнений с n неизвестными не равен нулю, то система совместна и имеет единственное решение, которое можно найти по формулам
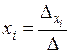 , (2.2)
, (2.2)
где i = 1, 2, 3,…, n, 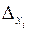 получается из определителя D путем замены i -го столбца определителя
получается из определителя D путем замены i -го столбца определителя 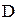 столбцом свободных членов.
столбцом свободных членов.
Замечание.
Теорема Крамера позволяет не только найти единственное решение системы, но и исследовать систему, не решая ее:
1) если D ¹ 0, то система имеет единственное решение;
2) если D = 0 и все 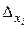 (i =1, 2, 3,…, n) тоже равны нулю, то система совместна, и имеет бесконечное множество решений.
(i =1, 2, 3,…, n) тоже равны нулю, то система совместна, и имеет бесконечное множество решений.
3) если D = 0 и хотя бы один из 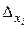 (i =1, 2, 3,…, n) не равен нулю, то система несовместна.
(i =1, 2, 3,…, n) не равен нулю, то система несовместна.
Пример 2.1. Решить систему 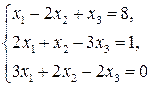
по формулам Крамера.
Решение
Найдем определитель системы по правилу треугольников:
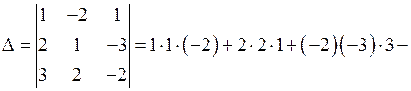
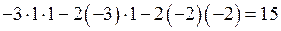 .
.
Так как D ¹ 0, то система имеет единственное решение.
Найдем это решение по формулам Крамера (2.2)
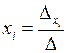 , i =1, 2, 3.
, i =1, 2, 3.
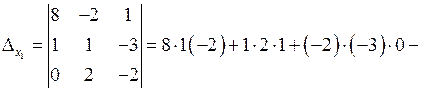
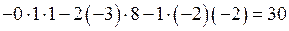 .
.
Примечание. В определителе D заменили первый столбец столбцом свободных членов.
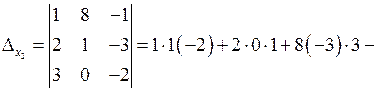
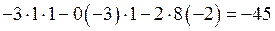 .
.
Примечание. В определителе D заменили второй столбец столбцом свободных членов.
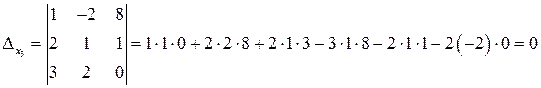 .
.
Примечание. В определителе D заменили третий столбец столбцом свободных членов.
Тогда

Итак, (2; – 3; 0) — решение системы.
Ответ: (2; – 3; 0).
Задачи для самостоятельного решения
Решить системы по формулам Крамера:
2.1. 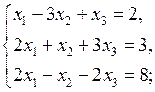 2.3.
2.3. 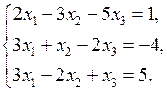
2.2. 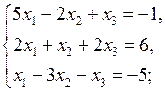
2.5. Определить, при каких значениях а и b система
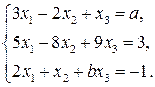
1) имеет единственное решение;
2) не имеет решений.
§ 2.3. Решение систем линейных уравнений
матричным методом
Рассмотрим неоднородную систему n линейных уравнений с n неизвестными
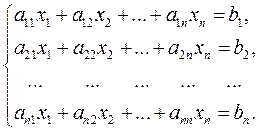 (2.3)
(2.3)
Введем обозначения:
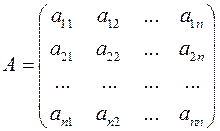
| — матрица системы, составленная из коэффициентов при неизвестных; |
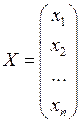 — матрица-столбец неизвестных;
— матрица-столбец неизвестных;
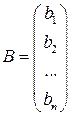 — матрица-столбец свободных членов.
— матрица-столбец свободных членов.
Тогда систему (2.3) можно записать в матричной форме
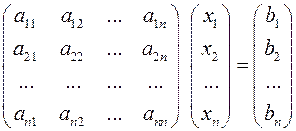 ,
,
т.е.
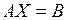 . (2.4)
. (2.4)
Если матрица А невырожденная, т.е. D А ¹ 0, то для нее существует обратная матрица А – 1.
Умножим обе части матричного уравнения (2.4) слева на А – 1, получим
А – 1(АХ) = А – 1 В.
Используя свойство ассоциативности произведения матриц, имеем
(А – 1 А) Х = А – 1 В.
Так как по определению обратной матрицы А – 1 А = Е, то
ЕХ = А – 1 В.
Так как ЕХ = Х, то
Х = А – 1 В. (2.5)
Пример 2.2. С помощью обратной матрицы решить систему уравнений
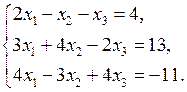
Решение
Введем обозначения:
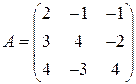 ;
; 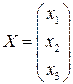 ;
; 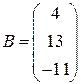 .
.
Тогда данная система уравнений записывается в матричной форме
 или АХ = В.
или АХ = В.
Его решение ищем по формуле (2.5):
Х = А – 1 В.
Найдем матрицу А – 1, обратную к матрице А.
Вычислим определитель матрицы А:
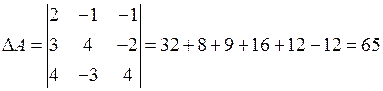 .
.
Так как D А ¹ 0, то матрица А невырожденная и, следовательно, имеет обратную матрицу А – 1.
Вычислим алгебраические дополнения всех элементов матрицы А:
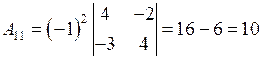 ;
;
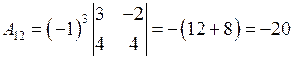 ;
;
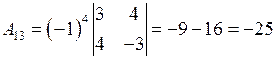 ;
;
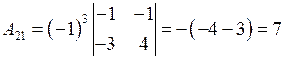 ;
;
 ;
;
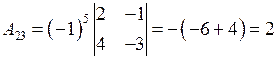 ;
;
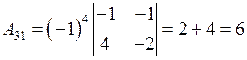 ;
;
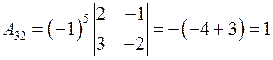 ;
;
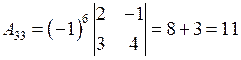 .
.
Составим матрицу А * из алгебраических дополнений:
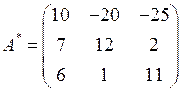 .
.
Транспонируем матрицу А * и получаем союзную матрицу 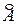 :
:
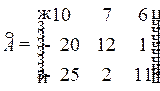 .
.
Находим обратную матрицу А -1 по формуле (1.1):
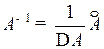 .
.
Тогда
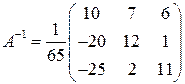 .
.
Находим матрицу-столбец неизвестных Х = А – 1 В по формуле (2.5):
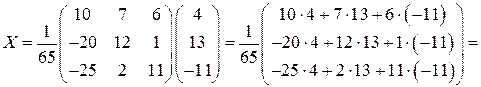
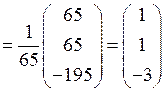 .
.
Итак,
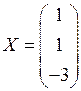 ,
,
т.е. х 1 = 1, х 2 = 1, х 3 = – 3.
Тогда (1; 1; – 3) — решение данной системы.
Ответ: (1; 1; – 3).
Рассмотрим решение других матричных уравнений.
Пример 2.3. Даны матрицы
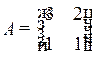 ,
, 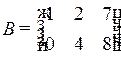 ,
, 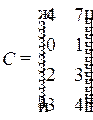 .
.
Решить матричные уравнения:
а) АХ = В; б) ХА = С.
1. Решение уравнения АХ = В находим по формуле (2.5):
Х = А – 1 В,
если D А ¹ 0.
Найдем обратную матрицу А – 1:
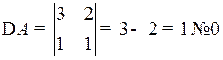 , то обратная матрица А – 1 существует.
, то обратная матрица А – 1 существует.
Алгебраические дополнения элементов матрицы А:
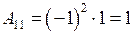 ;
; 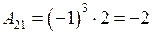 ;
;
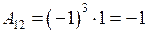 ;
; 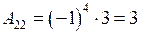 .
.
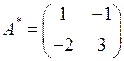
| — матрица из алгебраических дополнений элементов матрицы А. | |
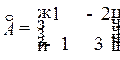
| — союзная матрица к матрице А. | |
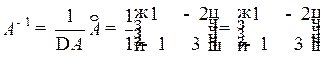
| — матрица, обратная к матрице А. | |
Тогда
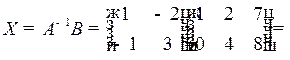
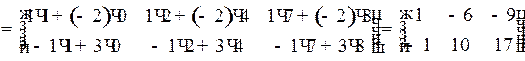 .
.
Ответ: 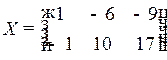 .
.
2. Чтобы решить матричное уравнение ХА = С, умножим обе части справа на обратную матрицу А –1:
(ХА
Date: 2015-07-25; view: 574; Нарушение авторских прав