
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Основные положения. Электрический ток в полупроводниках, как впрочем, и в любых других материалах, определяется концентрацией и подвижностью свободных носителей заряда
|
|
Электрический ток в полупроводниках, как впрочем, и в любых других материалах, определяется концентрацией и подвижностью свободных носителей заряда. Особенностью полупроводников является то, что их электропроводность в очень большой степени зависит от ничтожного количества примесей и от внешних энергетических воздействий.
В зависимости от степени чистоты различают собственные (можно пренебречь влиянием примесей при данной температуре) и примесные полупроводники.
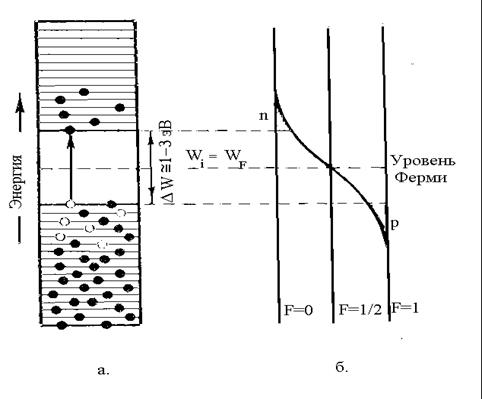
Электропроводность полупроводников целесообразно рассматривать с привлечением зонной теории твердого тела. На рис. 2.1, а приведена энергетическая диаграмма собственного полупроводника. Распределение электронов по энергиям в твердом теле в общем случае подчиняется статистике Ферми–Дирака. Вероятность нахождения электрона на уровне с энергией W определяется функцией
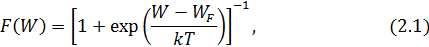
где W – энергия уровня, вероятность заполнения которого рассматривается; WF – энергия характеристического уровня, относительно которого кривая вероятности симметрична (уровень Ферми). При Т =0 К функция Ферми обладает следующими свойствами: при W ≤ WF F(W) = 1, при W > WF F(W) = 0 (рис. 2.1, б).
 |
Любой энергетический уровень может быть занят электроном либо оставаться свободным (занятым дыркой). Сумма вероятностей этих двух событий равна единице
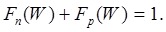 (2.2)
(2.2)
Вероятность заполнения энергетического уровня W электроном
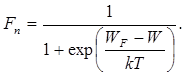 (2.3)
(2.3)
Функция вероятности для дырок Fp аналогична функции вероятности для электронов, но для дырок энергия возрастает при перемещении вниз от уровня Ферми.
В полупроводниках электрический ток переносят электроны, находящиеся в свободной зоне (зоне проводимости) и в валентной зоне (заполненной зоне). Соответственно, удельная проводимость полупроводника будет задаваться соотношением
γ = е (n μ n + p μ p), (2.4)
где е – заряд электрона; n и p – концентрации квазисвободных электронов и дырок соответственно; μ n и μ p – подвижность электронов и дырок, соответственно.
Концентрация свободных носителей зависит от температуры и расположения разрешенных уровней на энергетической зонной диаграмме полупроводника. При температуре абсолютного нуля Т =0 К квазисвободные носители в полупроводнике отсутствуют n = p = 0, следовательно отсутствует и проводимость γ = 0.
При повышении температуры часть электронов, обмениваясь энергией с колебаниями атомов кристаллической решетки (фононами), переходит на более высокие уровни энергии и попадает в зону проводимости (рис. 2.1, а). В результате концентрация свободных носителей n и p возрастает при увеличении температуры.
В собственных полупроводниках концентрации свободных электронов и дырок равны: nin = рin (индекс in – от английского intrinsic (собственный). Вероятность перехода электронов из валентной зоны в зону проводимости определяется шириной запрещенной зоны полупроводника ∆ W и температурой. Концентрацию электронов (дырок) определяют интегрированием по энергии произведения функции распределения плотности энергетических уровней в зоне проводимости и вероятности заполнения этих уровней электронами. Получают выражение для собственной концентрации носителей заряда
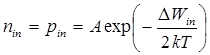 ; (2.5)
; (2.5)
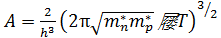 , (2.6)
, (2.6)
где k – постоянная Больцмана; h – постоянная Планка; Т – абсолютная температура; mn* и mp* – эффективные массы электрона или дырки, соответственно.
Величина A ~ T 3/2 представляет собой слабую функцию от температуры по сравнению с экспоненциальным множителем exp (- ∆ Win /2kT).
Анализ собственной электропроводности представляет теоретический интерес, поскольку дает представление о возможностях материала. Практический интерес представляют примесные полупроводники, эксплуатационные свойства которых определяются в основном примесями.
В примесных полупроводниках наряду с собственными носителями появляются дополнительные носители. Примеси создают дополнительные уровни в запрещенной зоне полупроводника.

|
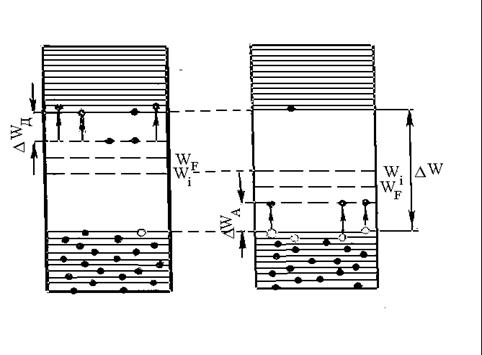
Концентрация примесей мала, расстояния между примесными атомами велико, их электронные оболочки не взаимодействуют друг с другом, соответственно примесные энергетические уровни являются дискретными, а не расщепляются в зону в отличие от уровней основных атомов (рис. 2.2).
При малой концентрации примесей вероятность непосредственного перехода электронов от одного примесного атома к другому ничтожна. Электроны переходят либо в зону проводимости с примесных донорных уровней (см. рис. 2.2, а) с образованием квазисвободных электронов (полупроводник n -типа), либо на примесные уровни акцепторов из валентной зоны (см. рис. 2.2, б) с образованием квазисвободных дырок в ней (полупроводник р -типа).
Концентрация примесных носителей задается соотношением
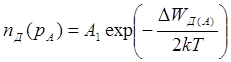 ; (2.7)
; (2.7)
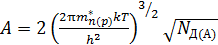 , (2.8)
, (2.8)
где ∆ W Д(А) – энергия ионизации доноров (акцепторов); N Д(А) – концентрация примесей доноров (акцепторов) в полупроводнике; индекс «Д» или «А» соответствует примесным носителям.
Энергия возбуждения свободных носителей в примесном полупроводнике много меньше, чем в собственном
∆ W Д(А) << ∆ W in.
Это приводит к тому, что ощутимые концентрации свободных носителей заряда в примесных полупроводниках появляются при существенно более низких температурах.
В случае донорных примесей ток обусловлен перемещением преимущественно электронов, имеем полупроводник n-типа:
n = nin + nд; р = рin; n >> р. (2.9)
В полупроводнике с акцепторными примесями ток обусловлен перемещением преимущественно дырок, имеем полупроводник p-типа:
р = рin + рд; n = nin; р >> n. (2.10)
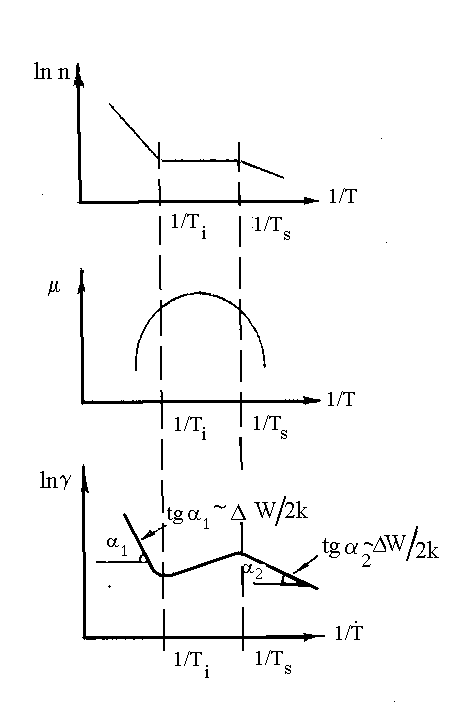
Зависимость концентрации носителей заряда от температуры. В общем случае на графике зависимости концентрации свободных носителей заряда от температуры для примесного полупроводника наблюдаются три участка (рис. 2.3, а).
В области низких температур (Т < Тs) ток обусловлен примесными носителями. График зависимости
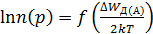 (2.11)
(2.11)
представляет собой прямую линию с тангенсом угла наклона, пропорциональным ∆ W Д(А). С увеличением температуры число носителей, поставляемых примесями, возрастает. Это происходит до тех пор, пока не истощатся электронные ресурсы примесных атомов.
В области средних температур (Тs < Т < Тi) все примеси уже ионизированы (истощены), а перехода электронов через запещенную зону еще не обнаруживается (собственных носителей еще мало). Участок кривой с постоянной концентрацией носителей заряда называется областью истощения примесей
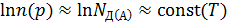 . (2.12)
. (2.12)
При высоких температурах (Т > Тi) начинается быстрый рост концентрации носителей вследствие перехода электронов через запрещенную зону. Концентрация собственных носителей превышает концентрацию примесных, то есть полупроводник из примесного становится собственным, хотя примеси в нем имеются. Наклон данного участка характеризует ширину запрещенной зоны полупроводника
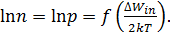 (2.13)
(2.13)
Температура насыщения примесей Тs может быть определена из условия
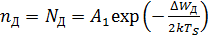 (2.14)
(2.14)
как 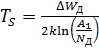 . (2.15)
. (2.15)
Температура перехода к собственной проводимости определяется из условия: nin = N Д, тогда
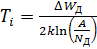 . (16)
. (16)

Зависимость подвижности носителей заряда от температуры. Кроме концентрации свободных носителей заряда на величину электропроводности оказывает влияние подвижность носителей, которая в общем виде может быть представлена соотношением:
μ ~ Тχ . (2.17)
Подвижность носителей определяется в основном двумя конкурирующими процессами, зависящими от температуры прямо противоположным образом (рис. 3.1, б). Эти два механизма приводят к наличию двух участков в кривой температурной зависимости подвижности.
В первом случае рассеяние носителей заряда происходит на ионизированных примесях (при столкновением носителей с ионизированными атомами примесей). При низких температурах интенсивность тепловых колебаний решетки невелика и преобладающим оказывается данный механизм. Показатель χ = 3/2 (μ ~ Т3/2).
Во втором случае рассеяние носителей заряда происходит при столкновении их с колеблющимися атомами кристаллической решетки полупроводника. Показатель χ = - 3/2 (μ ~ 1/Т3/2). При рассеянии носителей на тепловых колебаниях решетки средняя длина свободного пробега l ср одинакова для носителей с различными скоростями и обратно пропорциональна абсолютной температуре полупроводника.
Эти процессы протекают всегда одновременно, но при низких температурах преобладает рассеяние носителей на примесях, а при высоких – рассеяние на тепловых колебаниях решетки (фононах). Суммарная подвижность носителей тока определяется наиболее интенсивным процессом.
Зависимость удельной проводимости полупроводника от температуры. Поскольку зависимость подвижности носителей заряда от температуры носит степенной характер, а температурная зависимость концентрации носителей – экспоненциальная функция, то именно она, как более сильная, и будет в основном определять изменения удельной проводимости с температурой как при низких, так и при высоких температурах
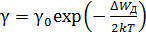 ;
; 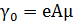 (2.18)
(2.18)
Данная зависимость, представленная в координатах lnγ = f (1/Т), приведена на рис. 2.3, в. Из участков примесной (Т < Тs) и собственной (Т > Тi) проводимости по тангенсу угла наклона прямых линий в координатах lnγ = f (1/Т) можно определить ширину запрещенных зон ∆W Д(А) и ∆Win соответственно. Для этого необходимо из графика определить tgα соответствующего участка
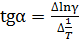 , (2.19)
, (2.19)
который с другой стороны определяется выражением
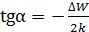 . (2.20)
. (2.20)
Таким образом, в общем случае температурная зависимость проводимости полупроводника имеет сложный характер (рис. 2.3, в). Для средних температур на участке истощения примесей в температурной зависимости проводимости будет проявляться зависимость подвижности носителей заряда от температуры и предэкспоненциальных множителей А или А 1.
При средних температурах по наклону прямой линии в координатах ln γ =f (ln T) можно определить показатель χв зависимости μ ~Т χ и сделать вывод о доминирующем механизме рассеяния.
Удельная электропроводность полупроводника так же, как и металла, может быть измерена четырехзондовым методом и рассчитана по формуле:
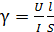 , (2.21)
, (2.21)
где S – площадь поперечного сечения кристалла полупроводника; l – расстояние между измерительными потенциальными зондами (2 и 3) (рис. 2.4); I – ток, протекающий между токовыми зондами (1 и 4); U – падение напряжения на длине l; U= 1/2 (|u 1 |+| u 2 |), а u 1и u 2 – падения напряжения, измеренные при двух противоположных направлениях протекания тока I (для устранения нелинейности вольт-амперной характеристики контакта металл-полупроводник).
Подробно методика применения четырехзондового метода приведена в описании к работе 3.
Date: 2015-07-25; view: 785; Нарушение авторских прав