Форми сигналів

За формою сигнали поділяються на неперервні та дискретні.

Неперервні сигнали можуть приймати неперервну множину значень (континуум) в певному інтервалі (в часі і за рівнем).

Дискретні сигнали описуються за допомогою кінцевого набору чисел або дискретних значень певної функції.

Тобто, неперервні сигнали (рис. 3.15, а) зображуються функцією, безперервною в часі на відрізку спостереження 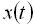, а дискретні (рис. 3.15, б) поступають тільки в певні моменти часу та зображаються дискретною функцією .

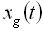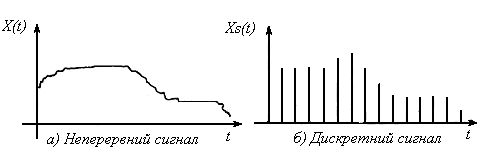
Рисунок 3.15 – Неперервні та дискретні сигнали

До елементарних детермінованих сигналів належить зокрема і одинична функція (стрибок).

При вивченні властивостей каналів передачі інформації, сигналів та завад абстрагуються від їх конкретної фізичної природи та призначення і оперують з їх моделями. Модель (англ. model) – це є вибраний спосіб опису об’єкта, процесу або явища, який відображає суттєві з погляду розв’язання даної задачі фактори. Оцінка електронних систем потребує виявлення кількісних співвідношень між основними параметрами джерела інформації і системи, тому дослідження здійснюється на математичних моделях.

Як відомо, інформація міститься в повідомленнях, зміст яких наперед невідомий і джерело інформації видає їх з певною ймовірністю. Передбачити точно зміну інформаційного параметра неможливо. Це означає, що інформаційний сигнал принципово являє собою випадкове коливання і його аналітичною моделлю може бути лише випадковий процес, який визначається імовірнісними характеристиками. Детерміноване коливання (сигнал) відображає відоме повідомлення, і немає сенсу його передавати. Йому відповідає модель у вигляді функції, що повністю визначена в часі. Разом з тим, вивчення моделей детермінованих сигналів дозволяє робити аналіз більш складних випадкових сигналів.

Сукупність детермінованих сигналів може подавати випадковий процес.

Навіть при експериментальному аналізі досить доречно вводити допоміжні функції (рис. 3.16).

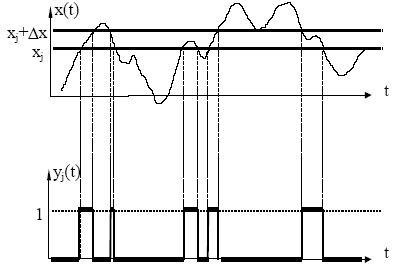
Рисунок 3.16 – Формування реалізацій 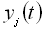випадкових функцій 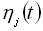з реалізації 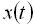випадкового процесу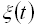

Існуючі аналізатори законів розподілу дозволяють визначати емпіричні функції розподілу та гістограми досліджуваних випадкових процесів. Блок-схема аналізатора наведена на рис. 3.17.

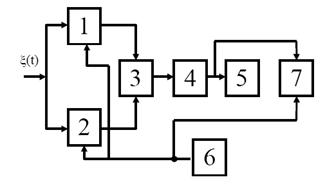
Рисунок 3.17 – Блок-схема аналізатора законів розподілу

Блок-схема складається з таких блоків:

1 – амплітудний селектор (компаратор) з порогом ;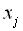

2 – амплітудний селектор (компаратор) з порогом ;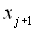

3 – пристрій віднімання;

4 – пристрій усереднення;

5 – індикатор;

6 – генератор пилкоподібної напруги;

7 – осцилограф.

Аналіз законів розподілу здійснюється, наприклад, для таких випадкових процесів як гаусів шум, синусоїдальний і пилкоподібний сигнал з випадковими фазами, адитивної суміші корисного сигналу та завади.

Спектральне подання випадкових сигналів

Розглянемо спектральне подання стаціонарних випадкових процесів. Стаціонарні випадкові процеси – це процеси, що протікають у часі однорідно, мають вигляд неперервних випадкових коливань навколо середнього значення .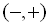

Якщо математичне сподівання, дисперсія, середнє квадратичне відхилення та кореляція є постійними, то такі процеси – стаціонарні.

Якщо існують випадкові процеси, що не витримують таких умов, але на деякому певному інтервалі відхиленням даних параметрів від константи можна знехтувати, то такий процес називають квазістаціонарним.

В будь-якій динамічній системі випадковий процес починається з так званого “перехідного” процесу і потім переходить в установлений режим, який з деяким наближенням можна вважати стаціонарним. Потрібно сказати, що стаціонарні випадкові процеси неперервні в часі, а значить не мають ні початку, ні кінця. Відомо два поняття: стаціонарність в обмеженому розумінні і стаціонарність у широкому.

Під стаціонарними процесами у вузькому смислі розуміють випадкові процеси, для яких функції розподілу щільності імовірності 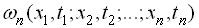вільного порядку 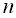не змінюються при будь-якому зсуві всієї групи точок повздовж осі часу

.

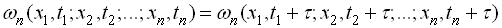З наведеного визначення можна сказати, що для стаціонарних процесів:

а) одновимірна функція розподілу щільності імовірності не залежить від часу

;

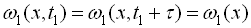б) двовимірна функція розподілу щільності імовірності залежить тільки від різниці часу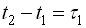

;

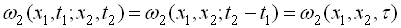в) тривимірна функція розподілу щільності імовірності залежить тільки від двох різниць часу 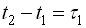та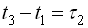

.

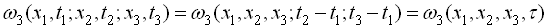Оскільки математичне сподівання і дисперсія виражаються через одновимірну функцію розподілу щільності імовірності, то для стаціонарного процесу математичне сподівання й дисперсія не залежать від часу. Унаслідок залежності двовимірної функції розподілу тільки від різниці часу 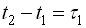, кореляційна функція стаціонарного процесу також залежить тільки від різниці часу .

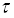Стаціонарною випадковою функцією в широкому смислі називається така випадкова функція 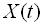, математичне сподівання якої постійне, а кореляційна функція залежить тільки від різниці аргументів, тобто

, ,

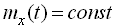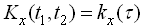де .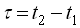

Дисперсія стаціонарної випадкової функції постійна

.

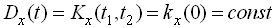Нормована кореляційна функція 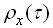стаціонарної випадкової функції 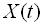має вигляд

.

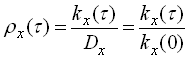Спектральне розкладання

,

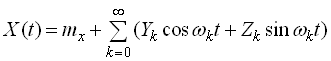де 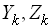, 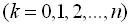– центровані некорельовані випадкові розміри.

Спектри потужності випадкових функцій визначаються аналогічно спектрам потужності детермінованих сигналів. Середня потужність випадкового процесу 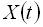, зареєстрованого в процесі однієї реалізації на інтервалі 0 - 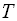з використанням рівності Парсеваля може бути обчислена за формулою:

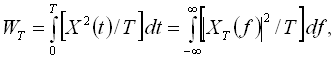
де 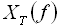– спектральна густина одиничної реалізації .

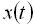При збільшенні інтервалу 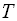енергія процесу на інтервалі необмежено наростає, а середня потужність прямує до певної границі:

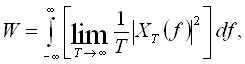
де підінтегральна функція є спектральною густиною потужності даної реалізації випадкового процесу:

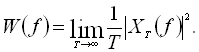
Досить часто цей вираз називають просто спектром потужності. Густина потужності є суттєвою, невід’ємною та парною функцією частоти. В загальному випадку густину потужності необхідно усереднювати за множиною реалізацій, але для ергодичних процесів допустимо усереднювати за однією тривалою в часі реалізацією.

Спектральна щільність будь-якої стаціонарної випадкової функції є невід’ємною функцією .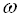

Спектральна щільність 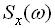і кореляційна функція 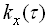пов’язані перетворенням Фур’є. У дійсній формі вони мають вигляд

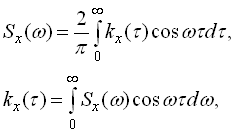
приймаючи, що 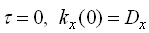отримаємо .

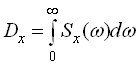Нормованою спектральною щільністю називається відношення спектральної щільності до дисперсії випадкової функції

.

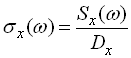Date: 2015-07-22; view: 426; Нарушение авторских прав