Випадкові сигнали та їх характеристики

Для опису випадкових процесів використовують методи теорії ймовірностей. У загальному випадку повною характеристикою випадкового процесу є його багатовимірна щільність імовірностей. Для стаціонарних гаусівських процесів одновимірна щільність імовірностей визначається дисперсією випадкового процесу. Для опису гаусівських процесів достатніми характеристиками є й кореляційна функція процесу. Однієї з характеристик випадкового сигналу є його спектральна щільність потужності, пов'язана з кореляційною функцією узагальненим перетворенням Фур'є.

Спектр випадкового процесу є суцільним. Для випадкових процесів з постійною спектральною щільністю й нескінченною смугою частот потужність нескінченна, а кореляційна функція є дельта-функцією. Такий процес має нескінченну дисперсію, є некорельованим і називається білим шумом. У випадкового процесу з постійною спектральною щільністю в обмеженій смузі частот потужність є скінченною і її можна визначити.

Отож, розглянемо дане питання більш детально. Під випадковим (стохастичним) процесом розуміють таку випадкову функцію часу 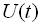, значення якої в кожен момент часу випадкові. Конкретний вигляд випадкового процесу, зареєстрованого у деякому досліді, називають реалізацією випадкового процесу. Дані, які характеризують всю множину можливих реалізацій називаються ансамблем.

Основними ознаками, за якими класифікують випадкові процеси є: простір станів, часовий параметр та статичні залежності між випадковими величинами 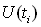в різні моменти часу .

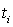Простором станів (англ. space of states) називають множину можливих значень випадкової величини 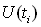. Випадковий процес у якому множини станів складають континуум, а зміна станів можлива в будь-які моменти часу, називають неперервним випадковим процесом. Якщо зміна станів допускається лише в кінцевому чи поточному числі моментів часу, то говорять про неперервну випадкову величину.

Відповідно до визначення випадковий процес 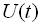може бути описаний системою 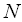звичайно залежних випадкових величин 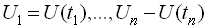, взятих в різні моменти часу 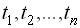. При необмеженому збільшенні числа 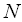така система еквівалентна випадковому процесу, що розглядається.

В більшості випадків для характеристики випадкових процесів використовують моментні функції перших двох порядків: математичне сподівання, дисперсію, а також кореляційну функцію

,

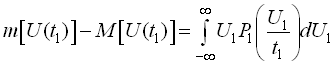де 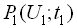– одновимірна щільність імовірності або одновимірна функція розподілення випадкового процесу. Фізико-математичне сподівання виражає значення сукупності вибірок випадкового процесу у визначений момент часу .

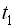Дисперсія – це математичне сподівання квадрата відхилення величини 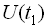від математичного сподівання у визначений момент часу .

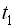Дисперсія виражається формулою

.

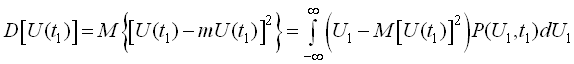Вона виражає розкид значення випадкової величини навколо математичного сподівання. Корінь квадратний з дисперсії прийнято називати середнім квадратичним відхиленням випадкової величини

.

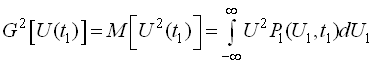Фізично початковий момент другого порядку є повною середньою потужністю випадкової величини.

Випадкові процеси можуть мати однакові математичні сподівання й дисперсію, але різко відрізняються за швидкістю зміни своїх значень у часі рис 3.14.

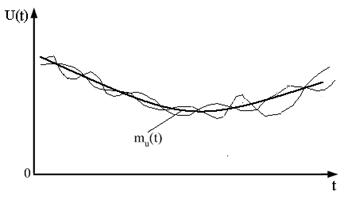
Рисунок 3.14 – Математичне сподівання для різних процесів

Тому для оцінювання ступеня статичної залежності миттєвих значень процесу 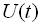в будь-які моменти часу 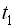та 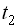використовується випадкова функція аргументів 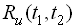, яка називається автокореляційною або просто кореляційною функцією.

При конкретних аргументах 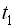та 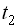вона дорівнює кореляційному моменту значень процесу 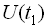та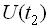

.

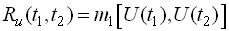Двовимірним законом розподілу випадкової функції 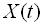називається закон розподілу 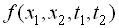системи двох випадкових розмірів 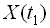та 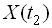, що є значеннями випадкової функції для різних значень аргументів 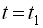та .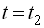

Математичним сподіванням випадкової функції 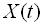називається невипадкова функція 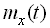, яка при кожному даному значенні аргументу дорівнює математичному сподіванню значення випадкової функції при тому ж значенні аргументу .

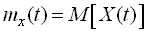Кореляційною функцією випадкової функції 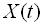називається невипадкова функція двох аргументів 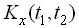, яка при кожній парі значень 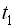та 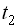дорівнює кореляційному моменту відповідних значень випадкової функції

,

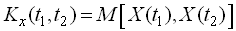де 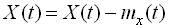– центрована випадкова функція.

При 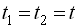кореляційна функція 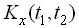перетворюється в дисперсію випадкової функції 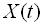, тобто

.

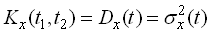Нормованою кореляційною функцією випадкової функції 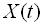називається функція

.

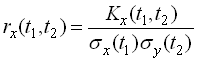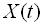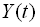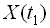Взаємною кореляційною функцією двох випадкових функцій та називається функція двох аргументів , яка при кожній довільно обраній парі їх значень дорівнює кореляційному моменту відповідних значень та 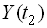цих випадкових функцій

.

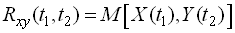Нормованою взаємною кореляційною функцією двох випадкових функцій 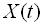та 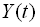називається функція

.

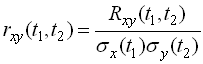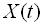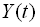Випадкові функції та називаються некаліброваними, якщо .

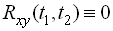Канонічним розкладанням випадкової функції 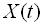називається подання її у вигляді

,

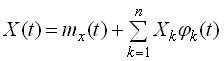де 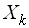, 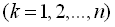– центрована некорельована випадкова величина з дисперсією 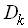; 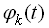– невипадкова функція.

Date: 2015-07-22; view: 316; Нарушение авторских прав