Средние величины и показатели вариации. В процессе обработки и обобщения статистических данных возникает необходимость определения средних величин

В процессе обработки и обобщения статистических данных возникает необходимость определения средних величин. Как правило, индивидуальные значения одного и того же признака из различных единиц совокупности неодинаковы.

Средняя величина – обобщающая характеристика изучаемого признака в исследуемой совокупности. Она отражает его типичный уровень в расчете на единицу совокупности в конкретных условиях места и времени.

Средней арифметической величиной называется такое среднее значение признака, при вычислении которого общий объем признака в совокупности сохраняется неизменным.

Иначе можно сказать, что средняя арифметическая величина – среднее слагаемое.

Средняя арифметическая бывает простая и взвешенная.

Средняя арифметическая простая равна сумме отдельных значений признака, деленной на число этих значений.

Отдельные значения признака называют вариантами и обозначают через х (х₁, х₂, х₃, …х_n), число единиц совокупности обозначают через n, среднее значение признака – через . Следовательно, средняя арифметическая простая равна:

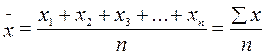. (1.1)

Простая средняя арифметическая применяется в случаях, когда имеются отдельные значения признака, т.е. данные не сгруппированы.

Если данные представлены в виде рядов распределения или группировок, то средняя исчисляется иначе:

, (1.2)

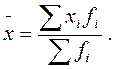(1.3)

Полученная формула называется средней арифметической взвешенной.

Из нее видно, что средняя зависит не только от значений признака, но и от их частот, т.е. от состава совокупности, от ее структуры

Анализ систематической вариации позволяет оценить степень зависимости изменений в изучаемом признаке от определяющих ее факторов. Например, изучая силу и характер вариации в выделяемой совокупности, можно оценить, насколько однородной является данная совокупность в количественном, а иногда и качественном отношении, а, следовательно, насколько характерной является исчисленная средняя величина. Степень близости данных отдельных единиц к средней измеряется рядом абсолютных, средних и относительных показателей.

К таким показателям относятся размах вариации, среднее линейное отклонение, дисперсия, среднее квадратическое отклонение, коэффициент вариации.

Размах вариации – это разность между наибольшим (Х _maх) и наименьшим (Х _min) значениями вариантов.

R = Х _maх – X _min. (1.4)

Безусловным достоинством этого показателя является простота расчета. Однако размах вариации зависит от величины только крайних значений признака, поэтому область его применения ограничена достаточно однородными совокупностями. В частности, на практике он находит применение в предупредительном контроле качества продукции.

Точнее характеризует вариацию признака показатель, основанный на учете колеблености всех значений признака. К таким показателям относятся среднее линейной отклонение, дисперсия и среднее квадратичное отклонение, представляющее собой среднюю арифметическую из отклонений индивидуальных значений признака от средней арифметической.

1. Среднее линейное отклонение d вычисляется по следующим формулам:

· для несгруппированных данных:

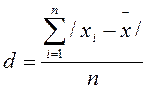, (1.5)

где х - индивидуальное значение признака;

- среднее значение признака в совокупности;

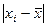- модуль отклонений каждой варианты х_i от средней

n – количество отклонений.

· для сгруппированных данных (среднее линейное отклонение взвешенное):

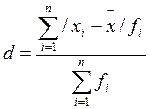, (1.6)

где f_i – частоты значений признака.

Дисперсия – это средняя арифметическая квадратов отклонений каждого значения признака от общей средней. В зависимости от исходных данных дисперсия может быть невзвешенной (простой) или взвешенной.

2. Дисперсия рассчитывается по следующим формулам:

· для несгруппированных данных:

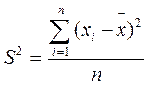; (1.7)

· для сгруппированных данных:

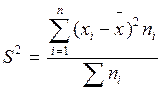(1.8)

Дисперсия обладает рядом свойств, некоторые из них позволяют упростить ее вычисления:

- дисперсия постоянной величины равна нулю;

- если все варианты значений признака уменьшить на одно и то же число, то дисперсия не уменьшится;

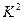- если все варианты значений признака уменьшить в одно и то же число раз ( раз), то дисперсия уменьшится в раз.

3. Среднее квадратичное отклонение S представляет собой корень квадратный из дисперсии:

· для несгруппированных данных:

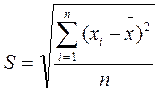; (1.9)

· для вариационного ряда:

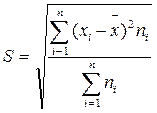. (1.10)

Размах вариации, среднее линейное и среднее квадратичное отклонение являются величинами именованными. Они имеют те же единицы измерения, что и индивидуальные значения признака.

Дисперсия и среднее квадратическое отклонение – наиболее широко применяемые показатели вариации. Кроме того, дисперсия может быть разложена на составные элементы, позволяющие оценить влияние различных факторов, обусловливающих вариацию признака.

При сравнении колеблемости различных признаков в одной и той же совокупности или же при сравнении колеблености одного и того же признака в нескольких совокупностях с различной величиной средней арифметической пользуются относительными показателями вариации. Этими показателями вычисляются как отношение абсолютных показателей вариации к средней арифметической (или медиане). Используя в качестве абсолютного показателя вариации размах вариации, среднее линейное отклонение, среднее квадратическое отклонение, получают относительные показатели колеблености (чаще всего они выражаются в процентах).

Коэффициент осцилляции отражает относительную колеблемость крайних значений признака вокруг средней.

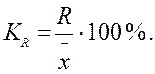(1.11)

Относительное линейное отклонение характеризует долю усредненного значения абсолютных отклонений от средней величины:

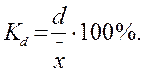(1.12)

Коэффициент вариации:

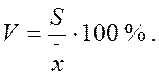(1.13)

Наиболее часто применяемый показатель относительной колеблености – коэффициент вариации. Его используют не только для сравнительной оценки вариации, но и для характеристики однородности совокупности. Совокупность считается однородной, если коэффициент вариации не превышает 33 %.

Date: 2015-07-24; view: 363; Нарушение авторских прав