
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Закон Ома, I, II законы Кирхгофа в дифференциальной форме
|
|
Выделим в проводящей среде небольшой параллелепипед объемом V (рис. 16.1).
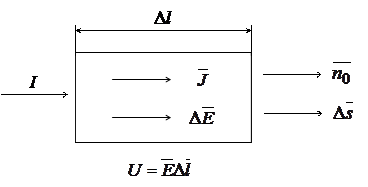 |
Рис. 16.1. Параллелепипед в проводящей среде
Длина ребер параллелепипеда D l, площадь поперечного сечения D s.
Расположим его так, чтобы напряженность поля была в нем направлена параллельно ребру. В силу малости объема можно считать, что напряженность поля одна и та же во всем элементарном объеме:
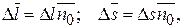
где 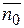 – единичный вектор по направлению
– единичный вектор по направлению 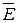 .
.
Ток:
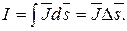 (16.2)
(16.2)
Напряжение на элементе объема:
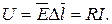 (16.3)
(16.3)
Сопротивление элемента объема:
 , (16.4)
, (16.4)
где g – удельная проводимость среды.
Поставив в (16.3) выражения (16.2) и (16.4) получим:
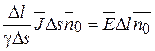 ,
,
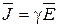 . (16.5)
. (16.5)
Выражение (16.5) называют законом Ома в дифференциальной форме. Это уравнение справедливо для областей вне источников ЭДС. В областях, занятых источниками ЭДС, существует также так называемое стороннее электрическое поле, обеспечивающее непрерывное движение зарядов в электрической цепи. Это поле обусловлено химическими, электрохимическими, тепловыми и термоэлектрическими процессами. Закон Ома в дифференциальной форме для областей, занятых источниками ЭДС
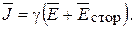 (16.6)
(16.6)
Уравнение (16.6) называется обобщенным законом Ома. Если от обеих частей взять интеграл по замкнутому контуру, то получим второй закон Кирхгофа в дифференциальной форме.
Если в проводящей среде выделить некоторый объем, по которому протекает постоянный, не изменяющийся во времени ток, то можно сказать, что ток, входящий в объем, равняется току, выходящему из объема, иначе в этом объеме происходило бы накопление электрических зарядов, что опыт не подтверждает. Математически это записывают так:
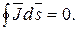 (16.7)
(16.7)
Разделим правую и левую часть уравнения (16.7) на объем и возьмем предел в случае, когда объем стремится к нулю
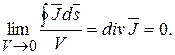 (16.8)
(16.8)
Соотношение (16.8) называется первым законом Кирхгофа в дифференциальной форме. Он гласит, что в установившемся режиме (при постоянном токе) в любой точке тока нет ни истока, ни стока линий тока проводимости 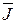 .
.
Date: 2015-07-24; view: 4974; Нарушение авторских прав