
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Текстовые задачи
|
|
Летнее домашнее задание
Преобразование тригонометрических выражений
Найдите значение выражения:
1.1 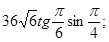 1.2
1.2  1.3
1.3 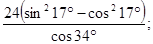
1.4  1.5
1.5 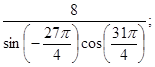 1.6
1.6 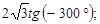
1.7 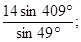 1.8
1.8 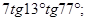 1.9
1.9 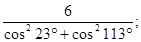
1.10 найти 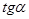 , если
, если 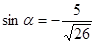 и
и 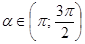 ;
;
1.11 найти 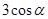 , если
, если 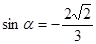 и
и 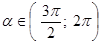 ;
;
1.12 найти 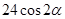 , если
, если 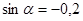 ; 1.13 найти
; 1.13 найти 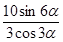 , если
, если 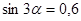 ;
;
1.14 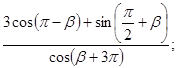 1.15 найти
1.15 найти 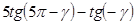 , если
, если 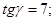
1.16 найти 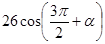 , если
, если 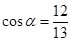 и
и 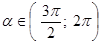 ;
;
1.17 найти  , если
, если 
1.18 найти 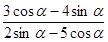 , если
, если 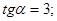
1.19 найти 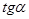 , если
, если 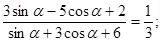
1.20 найти  , если
, если 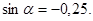
Текстовые задачи
2.1 В 2008 году в городском квартале проживало 20000 человек. В 2009 году, в результате строительства новых домов, число жителей выросло на 2%, а в 2010 году — на 3% по сравнению с 2009 годом. Сколько человек стало проживать в квартале в 2010 году?
2.2 Семья состоит из мужа, жены и их дочери студентки. Если бы зарплата мужа увеличилась вчетверо, общий доход семьи вырос бы на 165%. Если бы стипендия дочери уменьшилась вдвое, общий доход семьи сократился бы на 1%. Сколько процентов от общего дохода семьи составляет зарплата жены?
2.3 Митя, Антон, Паша и Гоша учредили компанию с уставным капиталом 100000 рублей. Митя внес 24% уставного капитала, Антон — 55000 рублей, Паша — 0,18 уставного капитала, а оставшуюся часть капитала внес Гоша. Учредители договорились делить ежегодную прибыль пропорционально внесенному в уставной капитал вкладу. Какая сумма от прибыли 600000 рублей причитается Гоше? Ответ дайте в рублях.
2.4 Смешали 8 литров 10-процентного водного раствора некоторого вещества с 12 литрами 40-процентного водного раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора?
2.5 Виноград содержит 90% влаги, а изюм — 5%. Сколько килограммов винограда требуется для получения 52 килограммов изюма?
2.6 Имеется два сплава. Первый сплав содержит 10% никеля, второй — 35% никеля. Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 30% никеля. На сколько килограммов масса первого сплава меньше массы второго?
2.7 Смешав 54-процентный и 61-процентный растворы кислоты и добавив 10 кг чистой воды, получили 46-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 56-процентный раствор кислоты. Сколько килограммов 54-процентного раствора использовали для получения смеси?
2.8 Смешали некоторое количество 20-процентного раствора некоторого вещества с таким же количеством 16-процентного раствора этого вещества. Сколько процентов составляет концентрация получившегося раствора?
2.9 Клиент А. сделал вклад в банке в размере 7600 рублей. Проценты по вкладу начисляются раз в год и прибавляются к текущей сумме вклада. Ровно через год на тех же условиях такой же вклад в том же банке сделал клиент Б. Ещё ровно через год клиенты А. и Б. закрыли вклады и забрали все накопившиеся деньги. При этом клиент А. получил на 836 рублей больше клиента Б. Какой процент годовых начислял банк по этим вкладам?
2.10 Из пункта A в пункт B одновременно выехали два автомобиля. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью 26 км/ч, а вторую половину пути — со скоростью, на 39 км/ч большей скорости первого, в результате чего прибыл в В одновременно с первым автомобилем. Найдите скорость первого автомобиля. Ответ дайте в км/ч.
2.11 Велосипедист выехал с постоянной скоростью из города А в город В, расстояние между которыми равно 88 км. На следующий день он отправился обратно в А со скоростью на 3 км/ч больше прежней. По дороге он сделал остановку на 3 часа. В результате велосипедист затратил на обратный путь столько же времени, сколько на путь из А в В. Найдите скорость велосипедиста на пути из В в А. Ответ дайте в км/ч.
2.12 Два велосипедиста одновременно отправились в 96-километровый пробег. Первый ехал со скоростью, на 4 км/ч большей, чем скорость второго, и прибыл к финишу на 4 часа раньше второго. Найти скорость велосипедиста, пришедшего к финишу первым. Ответ дайте в км/ч.
2.13 Из городов A и B, расстояние между которыми равно 310 км, навстречу друг другу одновременно выехали два автомобиля и встретились через 2 часа на расстоянии 170 км от города B. Найдите скорость автомобиля, выехавшего из города A. Ответ дайте в км/ч.
2.14 Расстояние между городами A и B равно 620 км. Из города A в город B выехал первый автомобиль, а через час после этого навстречу ему из города B выехал со скоростью 80 км/ч второй автомобиль. Найдите скорость первого автомобиля, если автомобили встретились на расстоянии 300 км от города A. Ответ дайте в км/ч.
2.15 Товарный поезд каждую минуту проезжает на 400 метров меньше, чем скорый, и на путь в 210 км тратит времени на 1 час больше, чем скорый. Найдите скорость товарного поезда. Ответ дайте в км/ч.
2.16 Расстояние между городами A и B равно 203 км. Из города A в город B выехал автомобиль, а через 3 часа следом за ним со скоростью 110 км/ч выехал мотоциклист, догнал автомобиль в городе C и повернул обратно. Когда он вернулся в A, автомобиль прибыл в B. Найдите расстояние от A до C. Ответ дайте в километрах.
2.17 Первый велосипедист выехал из поселка по шоссе со скоростью 13 км/ч. Через час после него со скоростью 10 км/ч из того же поселка в том же направлении выехал второй велосипедист, а еще через час после этого — третий. Найдите скорость третьего велосипедиста, если сначала он догнал второго, а через 3 часа 57 минут после этого догнал первого. Ответ дайте в км/ч.
2.18 Первую треть трассы автомобиль ехал со скоростью 60 км/ч, вторую треть – со скоростью 120 км/ч, а последнюю – со скоростью 110 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.
2.19 Первый час автомобиль ехал со скоростью 120 км/ч, следующий час — со скоростью 90 км/ч, а затем три часа — со скоростью 45 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.
2.20 Первые 120 км автомобиль ехал со скоростью 60 км/ч, следующие 120 км — со скоростью 80 км/ч, а затем 150 км — со скоростью 100 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.
2.21 Поезд, двигаясь равномерно со скоростью 60 км/ч, проезжает мимо придорожного столба за 57 секунд. Найдите длину поезда в метрах.
2.22 По двум параллельным железнодорожным путям друг навстречу другу следуют скорый и пассажирский поезда, скорости которых равны соответственно 80 км/ч и 40 км/ч. Длина пассажирского поезда равна 350 метрам. Найдите длину скорого поезда, если время, за которое он прошел мимо пассажирского поезда, равно 24 секундам. Ответ дайте в метрах.
2.23 Два человека отправляются из одного и того же места на прогулку до опушки леса, находящейся в 2,4 км от места отправления. Один идёт со скоростью 3 км/ч, а другой — со скоростью 4,2 км/ч. Дойдя до опушки, второй с той же скоростью возвращается обратно. На каком расстоянии от точки отправления произойдёт их встреча?
2.24 Дорога между пунктами А и В состоит из подъёма и спуска, а её длина равна 8 км. Пешеход прошёл путь из А в В за 2 часа 45 минут. Время его движения на спуске составило 1 час 15 минут. С какой скоростью пешеход шёл на спуске, если скорость его движения на подъёме меньше скорости движения на спуске на 2 км/ч? Ответ выразите в км/ч.
2.25 Два мотоциклиста стартуют одновременно в одном направлении из двух диаметрально противоположных точек круговой трассы, длина которой равна 6 км. Через сколько минут мотоциклисты поравняются в первый раз, если скорость одного из них на 18 км/ч больше скорости другого?
2.26 Из одной точки круговой трассы, длина которой равна 44 км, одновременно в одном направлении стартовали два автомобиля. Скорость первого автомобиля равна 112 км/ч, и через 48 минут после старта он опережал второй автомобиль на один круг. Найдите скорость второго автомобиля. Ответ дайте в км/ч.
2.27 Из пункта A круговой трассы выехал велосипедист, а через 30 минут следом за ним отправился мотоциклист. Через 10 минут после отправления он догнал велосипедиста в первый раз, а еще через 30 минут после этого догнал его во второй раз. Найдите скорость мотоциклиста, если длина трассы равна 30 км. Ответ дайте в км/ч.
2.28 Часы со стрелками показывают 6 часов 35 минут. Через сколько минут минутная стрелка в пятый раз поравняется с часовой?
2.29 Два гонщика участвуют в гонках. Им предстоит проехать 68 кругов по кольцевой трассе протяжённостью 6 км. Оба гонщика стартовали одновременно, а на финиш первый пришёл раньше второго на 15 минут. Чему равнялась средняя скорость второго гонщика, если известно, что первый гонщик в первый раз обогнал второго на круг через 60 минут? Ответ дайте в км/ч.
2.30 Моторная лодка прошла против течения реки 192 км и вернулась в пункт отправления, затратив на обратный путь на 4 часа меньше. Найдите скорость лодки в неподвижной воде, если скорость течения равна 2 км/ч. Ответ дайте в км/ч.
2.31 Пристани А и В расположены на озере, расстояние между ними 390 км. Баржа отправилась с постоянной скоростью из А в В. На следующий день после прибытия она отправилась обратно со скоростью на 3 км/ч больше прежней, сделав по пути остановку на 9 часов. В результате она затратила на обратный путь столько же времени, сколько на путь из А в В. Найдите скорость баржи на пути из А в В. Ответ дайте в км/ч.
2.32 Расстояние между пристанями А и В равно 120 км. Из А в В по течению реки отправился плот, а через час вслед за ним отправилась яхта, которая, прибыв в пункт В, тотчас повернула обратно и возвратилась в А. К этому времени плот прошел 24 км. Найдите скорость яхты в неподвижной воде, если скорость течения реки равна 2 км/ч. Ответ дайте в км/ч.
2.33 По морю параллельными курсами в одном направлении следуют два сухогруза: первый длиной 120 метров, второй — длиной 80 метров. Сначала второй сухогруз отстает от первого, и в некоторый момент времени расстояние от кормы первого сухогруза до носа второго составляет 400 метров. Через 12 минут после этого уже первый сухогруз отстает от второго так, что расстояние от кормы второго сухогруза до носа первого равно 600 метрам. На сколько километров в час скорость первого сухогруза меньше скорости второго?
2.34 Путешественник переплыл море на яхте со средней скоростью 18 км/ч. Обратно он летел на спортивном самолете со скоростью 414 км/ч. Найдите среднюю скорость путешественника на протяжении всего пути. Ответ дайте в км/ч.
2.35 Заказ на 182 детали первый рабочий выполняет на 1 час быстрее, чем второй. Сколько деталей в час делает второй рабочий, если известно, что первый за час делает на 1 деталь больше?
2.36 Двое рабочих, работая вместе, могут выполнить работу за 15 дней. За сколько дней, работая отдельно, выполнит эту работу первый рабочий, если он за 2 дня выполняет такую же часть работы, какую второй — за 3 дня?
2.37 Первая труба пропускает на 4 литра воды в минуту меньше, чем вторая. Сколько литров воды в минуту пропускает первая труба, если резервуар объемом 140 литров она заполняет на 8 минут дольше, чем вторая труба заполняет резервуар объемом 84 литра?
2.38 Каждый из двух рабочих одинаковой квалификации может выполнить заказ за 8 часов. Через 2 часа после того, как один из них приступил к выполнению заказа, к нему присоединился второй рабочий, и работу над заказом они довели до конца уже вместе. Сколько часов потребовалось на выполнение всего заказа?
2.39 Первый насос наполняет бак за 28 минут, второй — за 44 минуты, а третий — за 1 час 17 минут. За сколько минут наполнят бак три насоса, работая одновременно?
2.40 Игорь и Паша красят забор за 21 час. Паша и Володя красят этот же забор за 28 часов, а Володя и Игорь — за 36 часов. За сколько часов мальчики покрасят забор, работая втроем?
2.41 Первая труба наполняет резервуар на 16 минут дольше, чем вторая. Обе трубы наполняют этот же резервуар за 6 минут. За сколько минут наполняет этот резервуар одна вторая труба?
2.42 В помощь садовому насосу, перекачивающему 8 литров воды за 3 минуты, подключили второй насос, перекачивающий тот же объем воды за 6 минут. Сколько минут эти два насоса должны работать совместно, чтобы перекачать 20 литров воды?
2.43 Витя и Гриша выполняют одинаковый тест. Витя отвечает за час на 25 вопросов текста, а Гриша — на 30. Они одновременно начали отвечать на вопросы теста, и Витя закончил свой тест позже Гриши на 10 минут. Сколько вопросов содержит тест?
2.44 Плиточник должен уложить 280 м2 плитки. Если он будет укладывать на 6 м2 в день больше, чем запланировал, то закончит работу на 6 дней раньше. Сколько квадратных метров плитки в день планирует укладывать плиточник?
2.45 Две бригады, состоящие из рабочих одинаковой квалификации, одновременно начали строить два одинаковых дома. В первой бригаде было 20 рабочих, а во второй — 29 рабочих. Через 3 дня после начала работы в первую бригаду перешли 5 рабочих из второй бригады, в результате чего оба дома были построены одновременно. Сколько дней потребовалось бригадам, чтобы закончить работу в новом составе?
2.46 При двух одновременно работающих принтерах расход бумаги составляет 1 пачку за 12 минут. Определите, за сколько минут израсходует пачку бумаги первый принтер, если известно, что он сделает это на 10 минут быстрее, чем второй.
2.47 Рабочие прокладывают тоннель длиной 105 метров, ежедневно увеличивая норму прокладки на одно и то же число метров. Известно, что за первый день рабочие проложили 9 метров туннеля. Определите, сколько метров туннеля проложили рабочие в последний день, если вся работа была выполнена за 7 дней.
2.48 Турист идет из одного города в другой, каждый день проходя больше, чем в предыдущий день, на одно и то же расстояние. Известно, что за первый день турист прошел 9 километров. Определите, сколько километров прошел турист за пятый день, если весь путь он прошел за 9 дней, а расстояние между городами составляет 189 километров.
2.49 Компания "Альфа" начала инвестировать средства в перспективную отрасль в 2001 году, имея капитал в размере 4500 долларов. Каждый год, начиная с 2002 года, она получала прибыль, которая составляла 100% от капитала предыдущего года. А компания "Бета" начала инвестировать средства в другую отрасль в 2005 году, имея капитал в размере 5000 долларов, и, начиная с 2006 года, ежегодно получала прибыль, составляющую 300% от капитала предыдущего года. На сколько долларов капитал одной из компаний был больше капитала другой к концу 2009 года, если прибыль из оборота не изымалась?
2.50 Бизнесмен Бубликов получил в 2000 году прибыль в размере 5000 рублей. Каждый следующий год его прибыль увеличивалась на 300% по сравнению с предыдущим годом. Сколько рублей заработал Бубликов за 2003 год?
Date: 2015-07-24; view: 624; Нарушение авторских прав