Главная Случайная страница


Полезное:

Как сделать разговор полезным и приятным Как сделать объемную звезду своими руками Как сделать то, что делать не хочется? Как сделать погремушку Как сделать так чтобы женщины сами знакомились с вами Как сделать идею коммерческой Как сделать хорошую растяжку ног? Как сделать наш разум здоровым? Как сделать, чтобы люди обманывали меньше Вопрос 4. Как сделать так, чтобы вас уважали и ценили? Как сделать лучше себе и другим людям Как сделать свидание интересным?


Категории:

АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника






Резерфорд тəжірибесі

⇐ ПредыдущаяСтр 4 из 106Следующая ⇒

 

Альфа бөлшегінің шашырауын Резерфорд мынадай түрде түсіндірді. Яғни, альфа бөлшегі өте ауыр бөлшек, олай болса осындай ауыр бөлшекті үлкен бұрышқа шашырату үшін, оған өте ауыр оң зарядты бөлшектер əсер ету керек. Егер атом ішінде ондай бөлшек кездесетін болса, онда олардың арасында Кулондық күш əсер етеді:

 

F 2 Ze 2 (1.2.1)  
r 2  
     

мұндағы 2е - альфа бөлшегінің заряды, Ze - атом ішіндегі оң бөлшектің заряды.

 

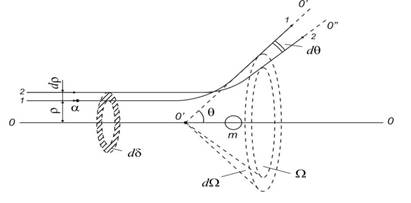
1.2-сурет

 

Осындай бөлшектердің əсерлесуін мынадай сызбамен көрсете аламыз (1.2-сурет). m - зерттелетін атом, ОО – түзудің бойында орналасқан. Осы түзуге параллель ρ – қашықтықта υ - жылдамдықпен альфа бөлшегі бағытталған болса, ол m - атомға жақындағанда, бастапқы бағытынан Ө-бұрышқа ауытқиды, ол

 

~ 16 ~


O O - пен OO - бағытының арасындағы ауытқу бұрышы болып табылады. Олай болса m - атомға (ядроға) жақын келген альфа бөлшегінің ауытқу бұрышының шамасы:

 

ctg     m        
  (1.2.2)  
  2 Ze 2  

 

мұндағы, – ең жақын келу қашықтығы (немесе нысаналы

 

қашықтық) деп аталады.

Егер атом ядросына альфа бөлшектің жақын келу қашықтығы -дан d дейін өзгерсе, онда шашырау бұрышы -дан

 

d -ға дейін өзгереді.                                          
Альфа бөлшектері         атом       ядросымен əсерлескенге  
дейін,көлденең қимасы dσ болатын сақина арқылы өтеді:    
        d 2 d               (1.2.3)  
оны эффективті қима деп атаймыз.               2 -    
(1.2.2) теңдікті     квадраттап,     одан тауып,  
дифференциалдайық                                                
          ctg 2           2     4     2      
            m            
                              4 Z 2 e 4        
                2 Ze 2                          
                                   
                                ctg       (1.2.4)  
        m   2          
                     
Сонда                                              
                                                 
  d 1   2 Ze           ctg                  
                         
                                   
                        d       (1.2.5)  
  m                              
                                   
                  sin                        
                                           

 


Осы (1.2.5) теңдікті (1.2.3) теңдікке қойсақ, онда

 

~ 17 ~


  1   2Ze 2 2 ctg               ctg       sin        
                       
  2               2 1 cos  
d2               d              
2   m 2     2                     2    
              sin 2           1 cos 2 sin   2  
                Ze2   2 d                    
2 sin d d                         ;                
                                   
                m 2       4                    
                                 
                          sin       2                  
                                                 



  Ze2 2 sin d      
2                  
m 2        
      4   (1.2.6)  
        sin   2    
               

 

Осы қимадан бірлік уақыт ішінде өтетін - бөлшегінің саны N болып, оған қарастырылып отырған заттың бірлік көлемінде n - ядро əсер етсе, онда d денелік бұрыш ішінде, -дан d дейін бұрылатын - бөлшегінің саны

 

        Ze 2     d      
                    (1.2.7)  
      m 2        
dN nN      
              sin          
                     
Бұл (1.2.7) Резерфорд формуласы деп аталады. Бұл  
формуладан dN ~     , яғни dN-нің шамасы - sin 4    
     
  sin 4      
                   
                     
                       

байланысты болады, егер шашырау бұрышы артса, онда dN-нің шамасы кемиді, олардың көбейтіндісі (·)

тұрақты болып қалады.

 

Осыларды қорыта келіп Резерфорд (өз теориясында) атомның ядролық моделінде электрон ядроны айнала үдей қозғалады деген тұжырымға келді. Сондықтан да бұл Э. Резерфорд модельін планетарлық модель деп атайды.


 

Жоғарыдағы (1.2.7) теңдеуді пайдалана отырып, атом ядросының зарядының мөлшерін табуға болады. Қалыпты жағдайда атом бейтарап, сондықтан оның ядросының заряды болуға тиіс, мұндағы Z-бүтін сан. Ол туралы түсінік кейінірек айтылады. Резерфордтың шəкірті Д. Чадвик тəжірибе жүзінде альфа бөлшегінің шашырауын бақылау арқылы Z(e)шамасын анықтады (мыс, күміс, платина, азот, т.б. үшін). Шашырау бұрышын анықтайтын (1.2.2) формула бойынша, альфа бөлшегінің ядроға ең жақын келу қашықтығын анықтады.

 

~ 18 ~


Сонымен атомның кішкене бөлігіне шоғырланған оң зарядталған атом ядросының радиусы 10-14 – 10-15 м шамасында, ал атом радиусы 10-10м, ядроның өлшемі атомынан жүз мың есе кіші, ядро заряды +Ze, сол ядроны айнала қозғалып жүрген электронның саны Z-ке тең деген қорытынды жасады.

 


⇐ Предыдущая12345678910Следующая ⇒





Date: 2015-07-24; view: 1651; Нарушение авторских прав


mydocx.ru - 2015-2024 year. (0.018 sec.) Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав - Пожаловаться на публикацию