Закон Ома. Сопротивление проводников

Законы постоянного тока

Закон Ома. Сопротивление проводников.

Закон Ома, открытый экспериментально, гласит: сила тока, протекающего по однородному проводнику, пропорциональна разности потенциалов на его концах (напряжению U):

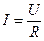, (4.1)

где R –величина электрического сопротивления проводника. Единицей сопротивления служит ом (Ом), равный сопротивлению такого проводника, в котором при напряжении 1 В течет ток силой 1 А.

Величина сопротивление R зависит от формы и размеров проводника, от его материала и температуры, а также — это следует помнить — от конфигурации (распределения) тока по проводнику. В случае провода смысл сопротивления не вызывает сомнений. В общем случае объемного распределения тока уже нельзя говорить о сопротивлении, пока не указаны или расположение подводящих к интересующему нас проводнику проводов, или конфигурация тока. Зависимость сопротивления от температуры устанавливает формула:

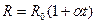(4.2),

где R₀ сопротивление проводника при 0º С, 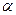− температурный коэффициент сопротивления, единица измерения в СИ (К^-1).

Проводники могут быть соединены последовательно и параллельно. При последовательном соединении n проводников (рис.4.1) общее сопротивление определяется так:

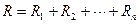(4.3)

Рис. 4.1 Последовательное соединение сопротивлений.

При параллельном соединении n проводников (рис.4.2) общее сопротивление равно

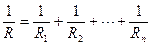(4.4)

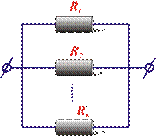
Рис.4.2 Параллельное соединение сопротивлений.

В простейшем случае однородного цилиндрического проводника сопротивление

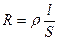, (4.5)

где l –длина проводника, S – площадь его поперечного сечения, -зависящий от свойств материала коэффициент, называемый удельным электрическим сопротивлением вещества. Если l =1 и S =1, то R численно равна . В СИ измеряется в Ом − метрах (Ом·м) Значения удельного электрического сопротивления для наиболее хороших проводников (медь, алюминий) составляют при комнатной температуре несколько единиц на 10^-8 Ом · м.

Закон Ома (4.1) и формула (4.5) позволяют найти силу тока в проволоках и вообще в тех случаях, когда трубки тока являются цилиндрами постоянного сечения. Однако часто приходится силу тока в проводящих средах, в которых трубки тока не имеют цилиндрической формы. Примерами могут служить сферический и цилиндрический конденсаторы, в которых пространство между обкладками заполнено проводящей средой. В этом случае формула (4.5) уже неприменима, так как расстояние l различно для разных точек поверхности обкладок, а площадь S имеет разную величину.

Однако закон Ома можно представить в другой форме, которая пригодна и для решения задач о токах в проводящих средах.

Рассмотрим в однородной и изотропной проводящей среде небольшой отрезок трубки тока длиной ∆ l (рис. 4.3) и два близких эквипотенциальных ее сечения 1 и 2. Обозначим их потенциалы через U₁ и U₂, а среднюю величину площади сечений – через ∆S

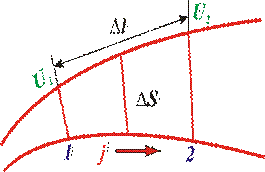
Рис.4.3. К закону Ома в дифференциальной форме

Применяя к этому отрезку закон Ома (4.1) и формулу (4.5), получим

,

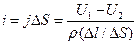или, сокращая на ∆S и вводя величину удельной электропроводности среды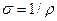

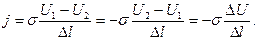
Чтобы последняя формула была совершенно точна, нужно перейти к пределу при ∆ l →0, так как только в этом случае рассматриваемый отрезок трубки можно считать цилиндрическим и применять формулу (4.5). Но

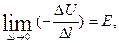
где Е – напряженность электрического поля внутри проводника.

Учитывая, что 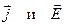векторы, и что внутри изотропных сред они направлены одинаково, находим окончательно

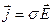(4.6)

Это соотношение носит название дифференциальной формы закона Ома. В отличие от (4.1) (интегральной формы закона Ома), оно содержит величины, характеризующие электрическое состояние среды в одной и той же точке. Иначе говоря, соотношение (4.6) выражает локальный закон Ома.

В анизотропных средах, каковыми являются многие кристаллы, направления 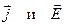, вообще говоря, уже не совпадают. В этом случае вместо формулы (4.6) получаются более сложные соотношения.

Величина называется удельной электрической проводимостью материала. Единица, обратная Ому, называется сименсом (См). Соответственно, единицей является сименс на метр (См / м)

Допустим для простоты, что в проводнике носители лишь одного знака. Согласно формуле (4.6) плотность тока в этом случае равна

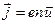(4.7)

Сравнение этого выражения с формулой (4.6) приводит к заключению, что скорость упорядоченного движения носителей тока пропорциональна напряженности поля, т.е. силе, сообщающей носителям упорядоченной движение. Пропорциональность скорости приложенной к телу силе наблюдается в тех случаях, когда кроме силы, вызвавшей движение, на тело действует сила сопротивления среды. Эта сила вызывается взаимодействием носителей тока с частицами, из которых построено вещество проводника. Наличие силы сопротивления упорядоченному движению носителей тока обуславливает электрическое сопротивление проводника.

Способность вещества проводить электрический ток характеризуется его удельным сопротивлением или удельной проводимостью . Эти величины определяются химической природой вещества и условиями, в частности температурой, при которых оно находится.

Для большинства металлов при температуре, близкой к комнатной изменяется аналогично R, т.е. 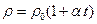и изменяется пропорционально термодинамической температуре Т

~ Т.

При низких температурах наблюдается отступление от этой зависимости (рис.4.4). В большинстве случаев зависимость от Т следует кривой 1.

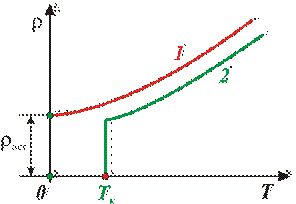
Рис.4.4. Зависимость удельного сопротивления от температуры

Остаточное сопротивление 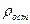в сильной степени зависит от чистоты металла и наличия остаточных механических напряжений в образце. Поэтому после отжига 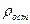заметно уменьшается. У абсолютно чистого металла с идеально правильной кристаллической решеткой при абсолютном нуле 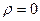. У большой группы металлов и сплавов при температуре порядка нескольких кельвинов сопротивление скачком обращается в нуль (кривая 2 на рис.4.4). Впервые это явление, названное сверхпроводимостью, было обнаружено в 1911г. Камерлинг-Оннесом для ртути. В дальнейшем сверхпроводимость была обнаружена у свинца, олова, цинка, алюминия и других металлов, а также у ряда сплавов. Для каждого сверхпроводника была обнаружена критическая температура Т_к, при которой он переходит в сверхпроводящее состояние. При действии на сверхпроводник магнитного поля сверхпроводящее состояние нарушается.

Зависимость электрического сопротивления от температуры положено в основу термометра сопротивления. Такой термометр представляет собой металлическую (обычно платиновую) проволочку, намотанную на фарфоровый или алюминиевый каркас. Проградуированный по постоянным температурным точкам термометр сопротивления позволяет измерить с погрешностью порядка нескольких сотых кельвин как низкие, так и высокие температуры. В последнее время все большее применение находят термометры сопротивления из полупроводников.

О заряде внутри проводника с током. Если ток постоянный, то избыточный заряд внутри однородного проводника всюду равен нулю (см. теорему Гаусса). Избыточный заряд может появиться только на поверхности однородного проводника, в местах соприкосновения с другими проводниками, а также там, где проводник имеет неоднородности.

Если токи стационарны, то распределение электрических зарядов в проводящей среде (вообще говоря, неоднородной) не меняется во времени, хотя и происходит движение зарядов: в каждой точке на место уходящих зарядов непрерывно поступают новые. Эти движущиеся заряды создают такое же кулоновское поле, что и неподвижные заряды той же конфигурации. Стало быть, электрическое поле стационарных токов — поле потенциальное.

Вместе с тем электрическое поле в случае стационарных токов существенно отличается от электростатического — кулоновского поля неподвижных зарядов. Последнее внутри проводников при равновесии зарядов равно нулю. Электрическое поле у стационарных токов есть также кулоновское поле, однако заряды, его возбуждающие, находятся в движении. Поэтому поле 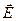у стационарных токов существует и внутри проводников с током.

Date: 2015-07-24; view: 605; Нарушение авторских прав