Пример построения двухмерного сечения в виде эллипса

При исследовании процесса получения сварных соединений (таблица 6.2) найдено уравнение регрессии второго порядка для 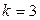, являющееся адекватной математической моделью:

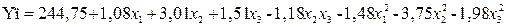(6.10)

Так как трудно представить геометрический образ для всех трех факторов, исследование проводится с помощью двух факторов, например, 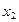и 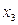. Фиксирование значения третьего фактора осуществляется на нулевом уровне, т.е. .

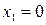Подставив в уравнение (6.10) значение 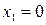, получают следующее уравнение:

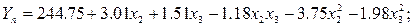(6.11)

Таблица 6.2 - Интервалы и уровни варьирования факторов для сварки материалов

Фактор	Обозначе-ние фактора	Уровень варьирования	Интервал варьиро-вания
нижний -1	нулевой 0	верхний +1
Давление на свариваемый материал, Па трикотажное полотно арт. 271304
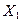
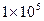
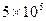
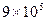
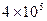
искусственная кожа арт. 023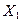
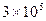
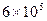
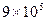
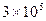
Время сварки, с:
трикотажное полотно арт. 271304		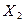0,5	3,5	6,5	3,0
искусственная кожа арт. 023		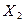3,0	5,0	7,0	2,0
Сила анодного тока, А		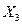0,55	0,75	0,95	0,2

Определяют координаты нового центра. Для этого уравнение дифференцируют это по 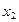и 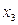и приравнивают частные производные нулю:

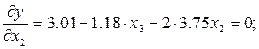
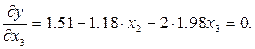
Вычисляют определитель системы:

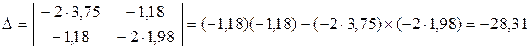
Определитель не равен нулю, следовательно, исследуемая поверхность имеет центр.

Решают систему уравнений (6.12) методом подстановки, вычисляют координаты нового центра в старых осях координат: , .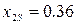

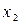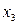Подставляя в уравнение (6.11) вместо и координаты центра 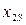и 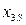, получают значение параметра оптимизации 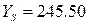в центре поверхности отклика:

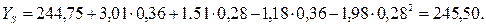
Переносим начало системы координат 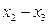в центр фигуры. При параллельном переносе системы координат в центр фигуры в исходном уравнении исчезают члены, содержащие линейные эффекты, и изменяется свободный член. Коэффициенты других членов не изменяются. В новой системе координат свободный член уравнения равен значению параметра оптимизации 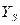в центре фигуры.

После переноса начала координат в новый центр уравнение примет вид:

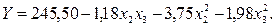(6.13)

Для исключения парного взаимодействия факторов определяют угол поворота осей координат в точке:

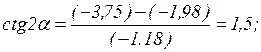
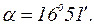
Далее определяют коэффициенты регрессии в канонической форме:

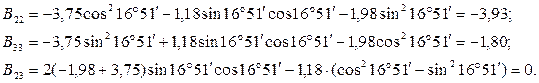
В результате получается уравнение в канонической форме

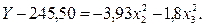(6.14)

Практика подтверждает точность расчетов (6.9):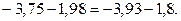

Проводятся старые оси координат 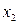и 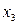. Граничные значения факторов соответствуют области их определения (в натуральных величинах). В этом примере фактор 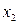– время сварки варьируется от 0,5 до 6,5, фактор 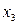– сила анодного тока – от 0,55 до 0,95 А (Таблица 6.3). Для нахождения нового центра в старых осях координат используют координаты 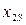и 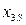. Переход от кодированных значений факторов к натуральным осуществляется по уравнению:

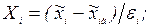(6.15)

где – натуральное значение 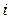-го фактора; 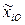– натуральное значение основного уравнения 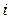-го фактора; 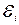– интервал варьирования 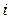-го фактора.

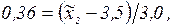
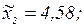
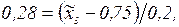
Координаты нового центра в старых осях координат в точке S(4,58; 0,81). Производится поворот осей координат в точке 0 на величину угла 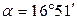, а затем параллельный перенос осей координат в новый центр (точку ).

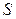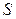
Построение линий равного значения отклика осуществляется в новой системе координат 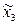. Значения параметра оптимизации выбираются через равные промежутки с учетом величин параметра оптимизации в области эксперимента.

При 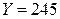уравнение (6.14) принимает вид:

.

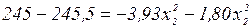Преобразуем это уравнение в стандартную форму:

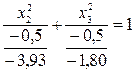или .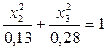

Оба коэффициента уравнения положительны, центр фигуры является максимумом, а вытянут эллипс вдоль оси 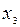(величина этого коэффициента минимальна).

Эллипс пересекается осью 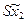в двух точках А(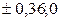), а с осью 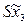– В(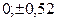). От точки 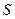по оси 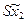откладывают вправо и влево величину 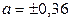; затем по оси 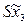величину 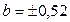в кодированных величинах (таблица). Полученные точки соединяют плавной кривой. Для более точного построения можно найти еще несколько промежуточных точек, например, задаемся значением 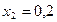и получаем точку С 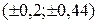и т.д. Аналогично строят другие контурные линии. Основой для построения служат данные табл. 6.3, получаемые подстановкой различных значений параметра оптимизации в уравнение (6.14).

Кривые с равными значениями параметра оптимизации – эллипса приведены на рис.6.1.

Таблица 6.3 – Данные для построения контурных кривых поверхности отклика

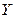
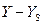
		Каноническое уравнение поверхности отклика	Величины полуосей
а	в
	-0,5		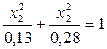0,36	0,52
	-1,5		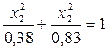0,62	0,91
	-2,5		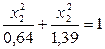0,8	1,18
	-3,5		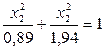0,94	1,39
	-4,5		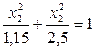1,07	1,58
	-5,5		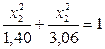1,18	1,75

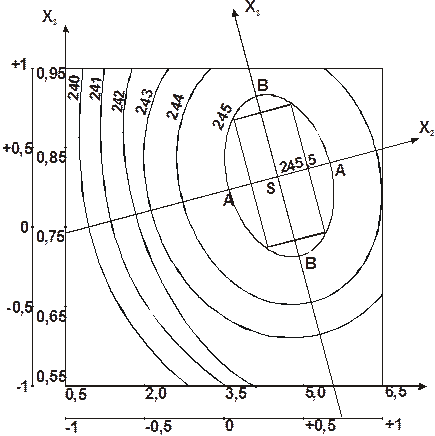
Рисунок6.1 – Контуры кривых с равными значениями

параметра оптимизации – эллипса

Вариант задания

По условию задачи (таблица 6.2) для математической модели процесса (объекта), выбранной в соответствии с вариантом задания (табл. 6.4), который определяется суммой двух последних цифр номера зачетной книжки студента, построить двухмерные сечения поверхностей отклика.

Таблица 6.4 - Варианты задания

№	Вид материала	Параметр оптимизации	Уравнение регрессии	Факторы
	Трикотажное полотно арт.	Прочность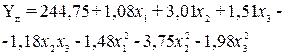
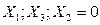
	Жесткость
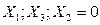
	Искусственная кожа арт.023	Прочность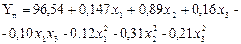
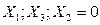
	Жесткость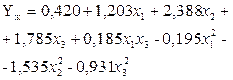

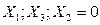
Содержание отчета по работе

1. Интервалы и уровни варьирования факторов для заданного варианта (табл. 6.2), уравнение регрессии.

2. Расчет координат нового центра и угла поворота осей координат в новом центре.

3. Уравнение регрессии в канонической форме.

4. Характеристика вида поверхности отклика.

5. Расчет данных для построения контурных кривых поверхности отклика, представленный в виде табл. 6.3.

6. Рисунок с сечениями поверхности отклика.

7. Выводы по работе.

Контрольные вопросы

1. С какой целью выполняется каноническое преобразование уравнений?

2. В чем заключается каноническое преобразование уравнений второй степени?

3. Как определяют положение нового центра в старых осях координат?

4. Как производится поворот осей координат?

5. Как определяют вид поверхности отклика?

6. Какова последовательность построения двухмерных сечений?

7. Какую информацию дает анализ семейства кривых?

Date: 2015-07-24; view: 740; Нарушение авторских прав