Канонический анализ математической модели

ЗАДАНИЕ 6

ПОСТРОЕНИЕ ГРАФИЧЕСКОЙ ЗАВИСИМОСТИ

МАТЕМАТИЧЕСКОЙ МОДЕЛИ

Канонический анализ математической модели

После получения адекватной математической модели объекта исследований можно получить наглядное представление о геометрическом образе изучаемой функции отклика построением соответствующей геометрической поверхности в двух- или трехмерном пространстве.

В результате выполнения плана второго порядка получают полином второй степени, адекватно описывающий область оптимума:

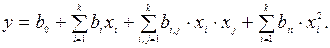(6.1)

Уравнение второй степени в таком виде анализировать сложно, поэтому путем преобразований его приводят к канонической форме. После канонического преобразования уравнения регрессии (при 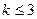) можно легко определить, к какому типу относится геометрический образ изучаемой функции отклика, пользуясь известными перечнями стандартных поверхностей второго порядка.

При 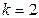геометрический образ изучаемой функции можно представить в виде контурных линий. Возможны четыре типа контурных линий. Каждая линия представляет собой проекцию сечений поверхности отклика плоскостью, параллельной плоскости чертежа при значениях параметра оптимизации, равных 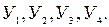Такие линии называют линиями равного отклика, так как каждая линия соответствует определенному значению параметра оптимизации. Контурные кривые, характеризующие область оптимума, описываемую уравнением второго порядка при числе факторов , приведены на рис. 6.1. Некоторые виды контурных поверхностей, характеризующие область оптимума, приведены в таблице 8.1.

С помощью уравнения регрессии в канонической форме все многообразие поверхностей отклика разделяют на три класса:

1) поверхности, имеющие экстремум – максимум или минимум (см. рис. 6.1,а, табл. 6.1, №1), в этом случае все коэффициенты канонического уравнения имеют одинаковые знаки, центр фигуры находится вблизи центра эксперимента;

2) поверхности типа минимакса (см. рис. 6.1,б, табл. 6.1, № 2, 3), коэффициенты канонического уравнения имеют разные знаки, центр фигуры находится вблизи центра эксперимента;

3) поверхности типа возрастающего возвышения или гребня (см. рис. 6.1, в, г, табл. 6.1, № 4, 8, 9), некоторые коэффициенты канонического уравнения близки к нулю, центр удалён от центра эксперимента.

Эллипсы соответствуют поверхности отклика, имеющей экстремум в центре (рис. 6.1 а). Коэффициенты 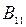и 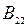имеют одинаковые знаки. Если они положительны, то центр фигуры является максимумом, а если отрицательны – минимумом. Эллипс вытянут по той оси, которой соответствует меньший по абсолютной величине коэффициент в каноническом уравнении. В этом случае значение параметра оптимизации увеличивается при движении от центра фигуры по одной оси и уменьшается при движении по другой.

Поверхность отклика в почти стационарной области характеризуется серией параллельных прямых, если один из коэффициентов канонического уравнения равен нулю (рис. 6.1 в).

Поверхность типа возрастающего возвышения («гребня») характеризуется контурными кривыми в виде парабол (рис. 6.1 г). Такая поверхность бывает, если один из коэффициентов канонического уравнения близок к нулю. Центр фигуры находится в бесконечности.

Гиперболы (рис. 6.1 б) соответствуют поверхности отклика типа минимакса.

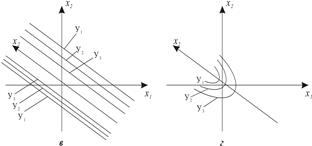
Рисунок 6.1 – Контурные кривые, полученные сечением поверхностей равных значений отклика: a – экстремум; б – минимакс; в – стационарное возвышение;

г – возрастающее возвышение

Таблица 6.1 - Поверхности отклика

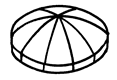
№ п/п	Схематическое изображение	Название поверхности	Каноническое уравнение
		Эллипсоид (в т.ч. Сфера и эллипсоид вращения)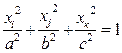
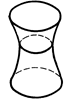
		Однополосный гиперболоид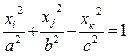
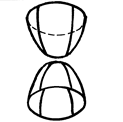
		Двухполосный гиперболоид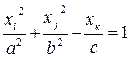
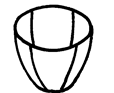
		Эллиптический параболоид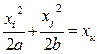
		Эллиптический цилиндр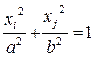
Окончание табл. 6.1
		Гиперболический параболоид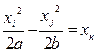
		Гиперболический цилиндр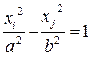
		Параблический цилиндр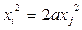
		Пара параллельных плоскостей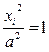

Date: 2015-07-24; view: 894; Нарушение авторских прав