Производная кинетической энергии по времени. Производную кинетической энергии по времени находим по правилу вычисления производной произведения и производной сложной функции

Производную кинетической энергии по времени находим по правилу вычисления производной произведения и производной сложной функции

.

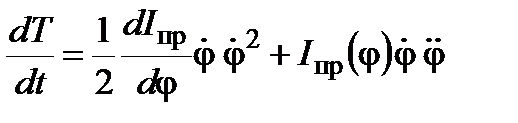Здесь

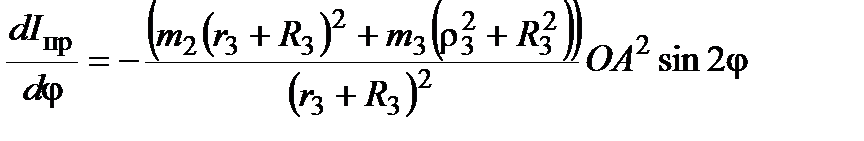
2.3. Элементарная работа и мощность внешних сил и работа внешних сил на конечном перемещении (механизм в горизонтальной плоскости)

В случае, когда механизм расположен в горизонтальной плоскости работу совершает только вращающий момент 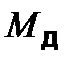. Элементарная работа при этом определяется равенством

.

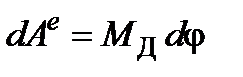Мощность

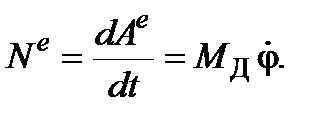
Работа при повороте маховика на угол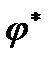

.

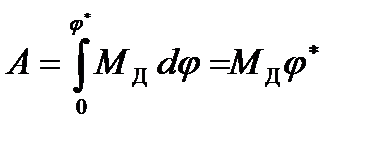2.4. Определение угловой скорости маховика при его повороте на угол φ*

Для определения угловой скорости маховика применяем теорему об изменении кинетической энергии в конечной форме, полагая, что механизм в начальный момент находился в покое.

, , .

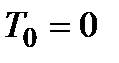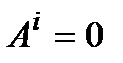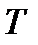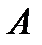Подстановка в это равенство найденных выражений и дает

,

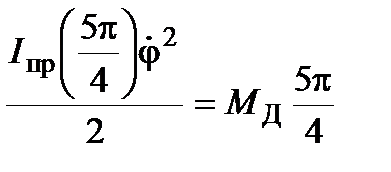где .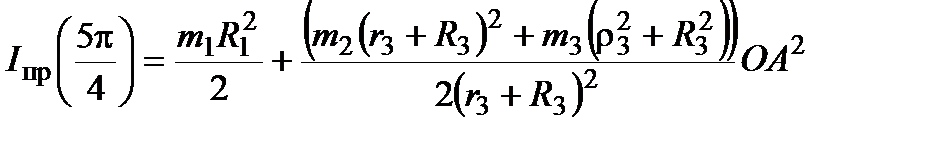

Тогда

.

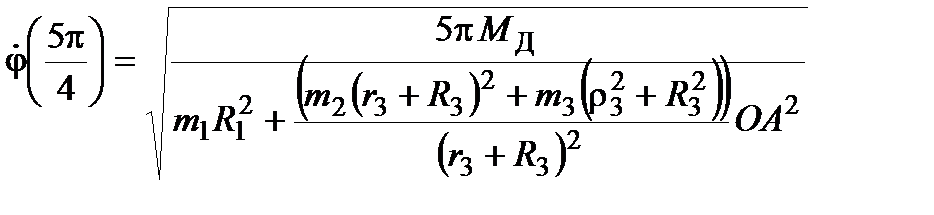2.5. Определение углового ускорения маховика при его повороте на угол φ*

Воспользуемся теоремой об изменении кинетической энергией в дифференциальной форме

, .

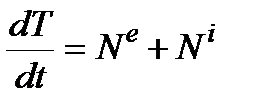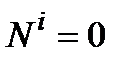Подставляя в это уравнение найденные выше значения, находим

.

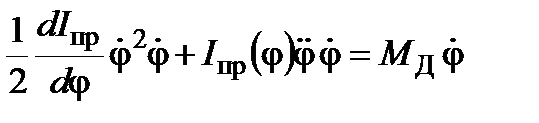Откуда

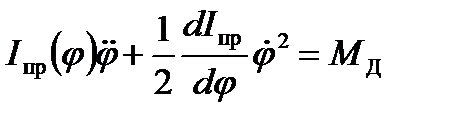(1)

и

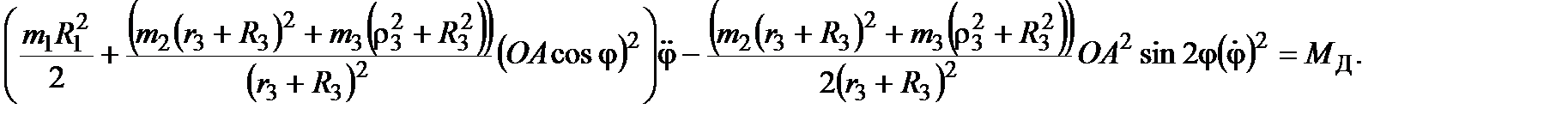
Это дифференциальное уравнение второго порядка описывает движение кулисного механизма. Оно может быть проинтегрировано только численно, а также использовано для нахождения углового ускорения маховика в произвольном его положении.

Определим угловое ускорение маховика при угле его поворота .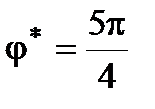

.

Date: 2015-07-24; view: 504; Нарушение авторских прав