Анализ отчетов

Программа Поиск решения (Solver) готовит три вида отчетов, торые характеризуют найденное решение задачи: отчет по результа-там, отчет по устойчивости и отчет по пределам. Ниже описывается структура отчетов и экономическая интерпретация результатов реше-ния оптимизационных задач менеджмента.

Геометрическая интерпретация задачи о красках

В этом разделе мы приводим простейшую геометрическую интер­претацию задачи о красках для того, чтобы читателю было проще ра зобраться с основными понятиями, используемыми в при анализе от четов.

Эта интерпретация иллюстрируется следующим графиком (рис. 1.3).

На осях координат отложены суточные объемы производства кра сок, определенные выше как содержимое изменяемых ячеек (см. По иск решения, Общие рекомендации по разработке структур ЭТ).

Тонкими линиями представлены ограничения для задачи о красках

ограничения по запасам продуктов:

Продукт П1; 1*Краска_Н + 2*Краска_В <= 6; (1

Продукт П2: 2* Краска_Н + 1* Краска_В <= 8; (2

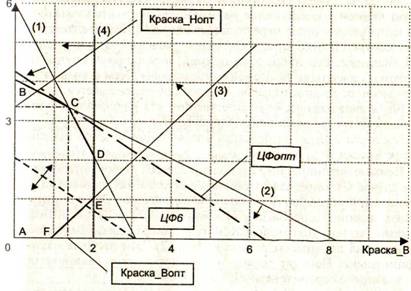
Рис. 1.3. Геометрическая интерпретация задачи о красках

ограничения по сбыту:

Краска_В <= Краска_Н+1; (3)

Краска_В <=2; <4)

Эти ограничения мы вводили в электронную таблицу (см. табл. 2).

На рис. 1.3 все прямые ограничений построены по отношениям (1)—(4), в которых знаки неравенства заменены знаками равенства. Маленькие стрелки на рисунке рядом с прямыми ограничений указы-вают на область, в которой действуют соответствующие ограничения. Например, для ограничения (4) это область левее прямой (4), т. е. диапазон, в котором Краска_В <= 2 (и, конечно, КраскаВ >= 0).

Пересечения прямых ограничений образуют область ABCDEF, в которой только и могут находиться оптимальные решения задачи. Эта область называется полигоном возможных решений.

Целевая функция (ЦФ) задана выражением

3*Краска_Н + 2*Краска_В,

которое уже использовалось Нами при составлении ЭТ. На рисунке приведена прямая ЦФ₆, определенная уравнением

3*Краска_Н + 2*Краска_В = 6,

32

Часть 1. Поиск решений на электронных таблицах

Анализ отчетов

33

т. е. для случая, когда ЦФ принимает значение 6 (тыс. долл.). Стрелки у этой прямой, указывающие на знаки «+» и «—», показывают, в ка­ком направлении будет перемещаться прямая ЦФ (параллельно самой себе) соответственно при увеличении значений ЦФ и уменьшении этих значений. Все точки этой прямой, находящиеся внутри полиго­на, будут удовлетворять ограничениям задачи. Чем больше прибыль, получаемая от продажи красок, тем дольше перемещается прямая ЦФ от ЦФ_б в направлении «+». Естественно, что максимальное значение прибыли будет наблюдаться в единственной точке полигона — точке С. Это точка и будет определять оптимальные объемы производства красок Краска_Н_0ПТ и Краска_В_опт.

Прямые ограничений, проходящие через точку оптимума (в на­шем случае С), определяют связанные ограничения, остальные прямые ограничений определяют несвязанные ограничения. Эти термины опре­деляют влияние запасов соответствующих ресурсов на оптимальное решение задачи. Для используемого примера связанными являются ограничения по запасам ресурсов (1) и (2). Эти ресурсы называются дефицитными. Понятие дефицитного ресурса тесно связано с поняти­ем связанного ограничения.

Изменение запасов дефицитного ресурса всегда изменяет значе­ние целевой функции и соответственно оптимальное решение задачи. Недефицитный ресурс не влияет на такое решение, но, разумеется, в определенных пределах. Для ситуации, изображенной на рис. 1.3, ре­сурс сбыта краски В (2 т в день, ограничение (4)) недефицитен. Но если спрос на этот вид краски начнет уменьшаться и достигнет вели­чины, меньшей значения Краска_В_опт, он станет дефицитным.

Из этого примера видно, что в зависимости от изменения условий производства и сбыта красок ресурсы могут менять свой статус, т. е. переходить из дефицитных в недефицитные, и наоборот. Возможно­сти таких изменений определяют устойчивость бизнес-процессов в системах менеджмента.

Коэффициенты в системе ограничений (1)—(4) и в ЦФ определяв ют углы наклона прямых на рисунке. Эти коэффициенты полностью определяются исходными данными задачи, вместе с тем вариации та­ких коэффициентов могут представлять самостоятельный интерес в исследовании систем менеджмента. Например, если в нашей задаче прямая ЦФ окажется параллельной прямой ограничения (2), то мак­симальному значению ЦФ будет соответствовать множество решений (все точки отрезка ВС на рисунке).

Эти и подобные им аспекты при проведении исследований на ЭТ анализируются на основе использования отчетов, создаваемых про-граммой поиска решений.

К сожалению, в общем случае для сложных задач с большим ко­личеством переменных столь наглядную геометрическую интерпрета­цию задачи поиска решения дать не удается.

Date: 2015-07-23; view: 446; Нарушение авторских прав