Как возвести матрицу в куб и более высокие степени?

Данные операции также определены только для квадратных матриц. Чтобы возвести квадратную матрицу 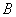в куб, нужно вычислить произведение:

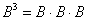
Фактически это частный случай умножения трёх матриц, по свойству ассоциативности матричного умножения: 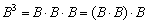. А матрица, умноженная сама на себя – это квадрат матрицы: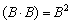

Таким образом, получаем рабочую формулу: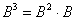

То есть задание выполняется в два шага: сначала матрицу необходимо возвести в квадрат, а затем полученную матрицу 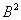умножить на матрицу .

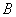Пример 8

Возвести матрицу 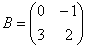в куб.

Это небольшая задачка для самостоятельного решения.

Возведение матрицы в четвёртую степень проводится закономерным образом:

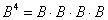
Используя ассоциативность матричного умножения, выведем две рабочие формулы. Во-первых: 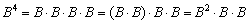– это произведение трёх матриц.

1) 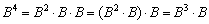. Иными словами, сначала находим , затем домножаем его на «бэ» – получаем куб, и, наконец, выполняем умножение ещё раз – будет четвёртая степень.

2) Но существует решение на шаг короче: 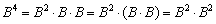. То есть, на первом шаге находим квадрат и, минуя куб, выполняем умножение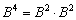

Дополнительное задание к Примеру 8:

Возвести матрицу 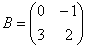в четвёртую степень.

Как только что отмечалось, сделать это можно двумя способами:

1) Коль скоро известен куб, то выполняем умножение .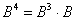

2) Однако, если по условию задачи требуется возвести матрицу только в четвёртую степень, то путь выгодно сократить – найти квадрат матрицы и воспользоваться формулой .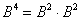

Оба варианта решения и ответ – в конце урока.

Аналогично матрица возводится в пятую и более высокие степени. Из практического опыта могу сказать, что иногда попадаются примеры на возведение в 4-ую степень, а вот уже пятой степени что-то не припомню. Но на всякий случай приведу оптимальный алгоритм:

1) находим ;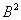
2) находим ;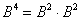
3) возводим матрицу в пятую степень: .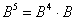

Вот, пожалуй, и все основные свойства матричных операций, которые могут пригодиться в практических задачах.

Во втором разделе урока ожидается не менее пёстрая тусовка.

Date: 2015-07-23; view: 2023; Нарушение авторских прав