
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Кут між прямою і площиною. Умови паралельності та перпендикулярності прямої і площини
|
|
Кутом між прямою і площиною називається кут між цією прямою та її проекцією на дану площину. Нехай площина П і пряма 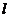 задані рівняннями
задані рівняннями
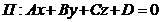 і
і 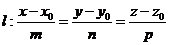 .
.
Позначимо гострий кут між прямою 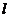 та її проекцією
та її проекцією 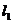 на площину П (рис. 4) через j, а кут між нормальним вектором
на площину П (рис. 4) через j, а кут між нормальним вектором 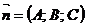 площини П та напрямним вектором
площини П та напрямним вектором 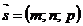 прямої
прямої 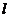 – через
– через 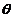 . Якщо
. Якщо 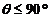 , то
, то 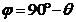 , тому
, тому 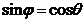 ; якщо ж
; якщо ж 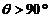 , то
, то 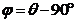 і
і 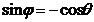 . Отже, в будь-якому випадку
. Отже, в будь-якому випадку 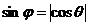 . Але
. Але 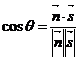 , тому кут між прямою і площиною знаходиться за формулою
, тому кут між прямою і площиною знаходиться за формулою

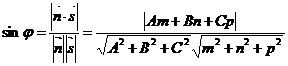 (14)
(14)
Приклад. 6. Обчислити кут між прямою 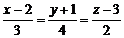 і площиною
і площиною 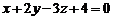 .
.
… Використаємо формулу (14), в якій А= 1, В= 2, С=- 3, m= 3, n= 4, p= 2, то
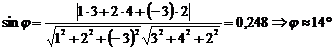 . †
. †
Якщо пряма 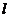 і площина П паралельні, то вектори
і площина П паралельні, то вектори 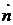 і
і 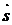 перпендикулярні, тому
перпендикулярні, тому 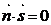 , тобто
, тобто
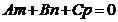 . (15)
. (15)
Формула (15) називається умовою паралельності прямої і площини.
Приклад 7. Довести, що пряма 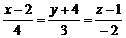 паралельна площині
паралельна площині 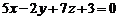 .
.
… Нормальний вектор площини має координати 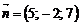 , а напрямний вектор прямої –
, а напрямний вектор прямої – 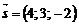 . Знайдемо їхній скалярний добуток
. Знайдемо їхній скалярний добуток 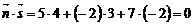 і за формулою (15) отримаємо, що дана пряма і площина паралельні, що і треба було довести. †
і за формулою (15) отримаємо, що дана пряма і площина паралельні, що і треба було довести. †
Якщо пряма 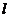 перпендикулярна площині П, то вектори
перпендикулярна площині П, то вектори 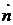 і
і 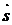 паралельні, тому має місце співвідношення
паралельні, тому має місце співвідношення
 , (15)
, (15)
яке називається умовою перпендикулярності прямої і площини.
Приклади. 8. Скласти рівняння площини, яка проходить через точку  перпендикулярно прямій
перпендикулярно прямій 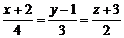 .
.
… Очевидно, що за нормальний вектор  шуканої площини можна взяти паралельний йому напрямний вектор прямої
шуканої площини можна взяти паралельний йому напрямний вектор прямої 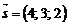 . Залишається використати формулу (11.3) – рівняння площини, яка проходить через точку перпендикулярно вектору
. Залишається використати формулу (11.3) – рівняння площини, яка проходить через точку перпендикулярно вектору 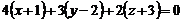 або
або 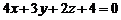 . †
. †
Через точку 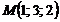 провести пряму, перпендикулярну площині
провести пряму, перпендикулярну площині 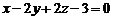 . Обчислити напрямні косинуси цієї прямої.
. Обчислити напрямні косинуси цієї прямої.
… Візьмемо за напрямний вектор шуканої прямої паралельний йому нормальний вектор 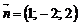 даної площини. Знаючи координати точки, через яку проходить пряма та її напрямний вектор, запишемо за формулою (3) канонічні рівняння цієї прямої
даної площини. Знаючи координати точки, через яку проходить пряма та її напрямний вектор, запишемо за формулою (3) канонічні рівняння цієї прямої 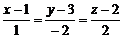 . Напрямні косинуси прямої знайдемо за формулою (5):
. Напрямні косинуси прямої знайдемо за формулою (5):
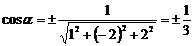 ,
, 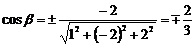 ,
, 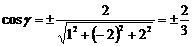 . †
. †
Для визначення точки перетину площини П і прямою 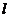 , які задані рівняннями
, які задані рівняннями 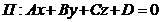 і
і 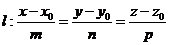 , потрібно скласти параметричні рівняння прямої, розв’язати систему, складену з отриманих рівнянь прямої та рівняння площини, і проаналізувати її:
, потрібно скласти параметричні рівняння прямої, розв’язати систему, складену з отриманих рівнянь прямої та рівняння площини, і проаналізувати її:
§ якщо
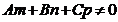 (16)
(16)
маємо умову перетину прямою площини;
§ якщо 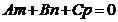 і
і 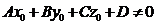 , то пряма паралельна площині;
, то пряма паралельна площині;
§ якщо
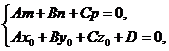 (17)
(17)
то маємо умову належності прямої площині.
Приклади. 9. Знайти точку перетину прямої  з площиною
з площиною 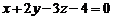 .
.
… Запишемо рівняння прямої в параметричній формі: поклавши 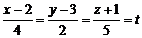 , отримаємо
, отримаємо 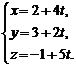 Підставивши отримані значення змінних х, у, z в рівняння площини, маємо
Підставивши отримані значення змінних х, у, z в рівняння площини, маємо 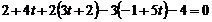 , звідки
, звідки 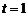 . Підставивши тепер отримане значення в параметричні рівняння прямої, отримаємо
. Підставивши тепер отримане значення в параметричні рівняння прямої, отримаємо 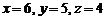 . Отже,
. Отже, 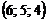 – шукана точка перетину прямої і площини. †
– шукана точка перетину прямої і площини. †
Довести, що пряма 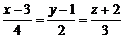 лежить в площині
лежить в площині 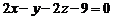 .
.
… Використовуючи умову (17), коли 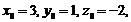
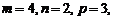
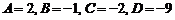 , знаходимо
, знаходимо 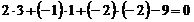 і
і 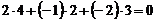 , отже, умови (17) виконуються, значить, пряма лежить в площині, що і треба було довести. †
, отже, умови (17) виконуються, значить, пряма лежить в площині, що і треба було довести. †
11.27. Скласти рівняння площини, що проходить через пряму  і точку
і точку 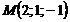 .
.
… Використовуючи рівність (11.10), запишемо рівняння пучки площин, що проходять через дану пряму: 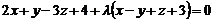 . Так як координати точки М повинні задовольняти рівняння площини, то підставивши їх в отримане співвідношення
. Так як координати точки М повинні задовольняти рівняння площини, то підставивши їх в отримане співвідношення 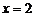 ,
, 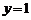 ,
, 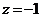 , маємо
, маємо 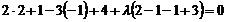 , або
, або 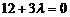 , звідки
, звідки 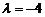 . Підставляючи тепер в рівняння пучки значення
. Підставляючи тепер в рівняння пучки значення 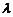 , одержимо
, одержимо 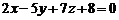 . †
. †
З початку координат опустити перпендикуляр на пряму 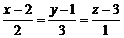 .
.
… Використовуючи умову (15) перпендикулярності прямої і площини та поклавши 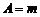 ,
, 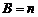 ,
, 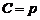 ,
,  , складемо рівняння площини, що проходить через початок координат і є перпендикулярною заданій прямій. Це рівняння має вигляд
, складемо рівняння площини, що проходить через початок координат і є перпендикулярною заданій прямій. Це рівняння має вигляд 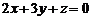 . Знайдемо точку перетину отриманої площини і заданої прямої. Параметричне рівняння прямої записується так:
. Знайдемо точку перетину отриманої площини і заданої прямої. Параметричне рівняння прямої записується так: 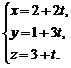 . Для визначення t маємо рівняння
. Для визначення t маємо рівняння 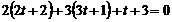 , звідки
, звідки 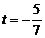 . Координати точки перетину
. Координати точки перетину 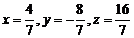 , тобто
, тобто  . Залишається скласти рівняння прямої, що проходить через початок координат і через точку М; використовуючи співвідношення (6), отримаємо
. Залишається скласти рівняння прямої, що проходить через початок координат і через точку М; використовуючи співвідношення (6), отримаємо 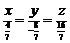 або
або 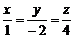 . †
. †
Знайти точку N, симетричну точці 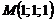 відносно площини
відносно площини 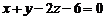 .
.
… Запишемо рівняння довільної прямої, що проходить через точку М:  . Координати
. Координати 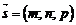 напрямного вектора прямої, перпендикулярної площині, можна замінити координатами нормального вектора
напрямного вектора прямої, перпендикулярної площині, можна замінити координатами нормального вектора 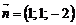 цієї площини. Тоді рівняння цієї прямої запишеться у вигляді
цієї площини. Тоді рівняння цієї прямої запишеться у вигляді 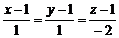 . Знайдемо проекцію точки М на дану площину, розв’язавши систему
. Знайдемо проекцію точки М на дану площину, розв’язавши систему  Перепишемо рівняння прямої в параметричному вигляді
Перепишемо рівняння прямої в параметричному вигляді 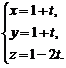 Підставляючи ці вирази в рівняння площини, знайдемо
Підставляючи ці вирази в рівняння площини, знайдемо 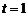 , звідки
, звідки 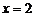 ,
, 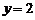 ,
, 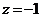 . Координати симетричної точки знайдемо з формул
. Координати симетричної точки знайдемо з формул 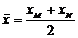 ,
, 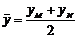 ,
, 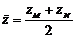 , тобто
, тобто 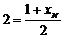 ,
, 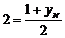 ,
,  , отже,
, отже, 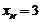 ,
, 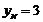 ,
, 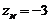 . Значить,
. Значить, 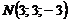 . †
. †
Знайти точку N, симетричну точці 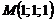 відносно прямої
відносно прямої  .
.
… Рівняння площини, що проектує точку М на дану пряму, має вигляд 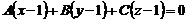 . Координати нормального вектора
. Координати нормального вектора 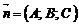 площини, перпендикулярної прямій, замінимо координатами напрямного вектора
площини, перпендикулярної прямій, замінимо координатами напрямного вектора 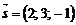 даної прямої; тоді отримаємо
даної прямої; тоді отримаємо 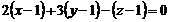 або
або 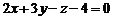 . Знайдемо проекцію точки М на пряму, для чого розв’яжемо систему рівнянь
. Знайдемо проекцію точки М на пряму, для чого розв’яжемо систему рівнянь 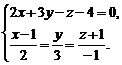 Параметричні рівняння даної прямої мають вигляд
Параметричні рівняння даної прямої мають вигляд 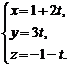 Підставляючи x, y і z площини, знайдемо
Підставляючи x, y і z площини, знайдемо 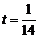 . Звідси
. Звідси  ,
, 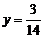 ,
, 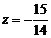 . Тоді координати симетричної точки можна знайти, використовуючи формули для координат середини відрізка
. Тоді координати симетричної точки можна знайти, використовуючи формули для координат середини відрізка 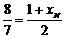 ,
, 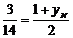 ,
, 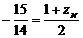 , звідки
, звідки 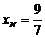 ,
, 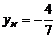 ,
, 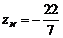 , отже,
, отже, 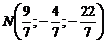 . †
. †
. Через пряму 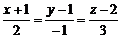 провести площину, паралельну прямій
провести площину, паралельну прямій 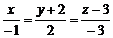 .
.
… Запишемо рівняння першої із заданих прямих за допомогою рівняння двох площин, що проектують її відповідно на площини Оху і Oyz:
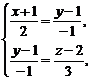 або
або 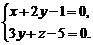
Рівняння пучки площин, що проходять через цю пряму, має вигляд 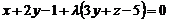 або
або 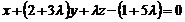 . Використовуючи умову паралельності прямої і площини, визначимо
. Використовуючи умову паралельності прямої і площини, визначимо 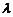 так, щоб відповідна площина пучки була паралельною другій із заданих площин. Маємо
так, щоб відповідна площина пучки була паралельною другій із заданих площин. Маємо 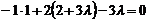 , або
, або 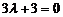 , звідки
, звідки  . Таким чином, шукана площина визначається рівнянням
. Таким чином, шукана площина визначається рівнянням 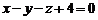 . †
. †
Знайти рівняння проекції прямої 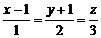 на площину
на площину 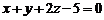 .
.
… Запишемо рівняння заданої прямої у вигляді рівнянь двох площин, що проектують її відповідно на площини Оху і Oхz:
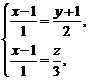 або
або 
Рівняння пучки площин, що проходять через дану пряму, має вигляд 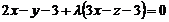 або
або 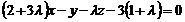 . Використовуючи умову перпендикулярності площин, виберемо з цієї пучки площину, яка проектує дану пряму на задану площину. Маємо
. Використовуючи умову перпендикулярності площин, виберемо з цієї пучки площину, яка проектує дану пряму на задану площину. Маємо 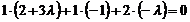 , або
, або 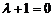 , звідки
, звідки  . Отже, рівняння площини, що проектує пряму, має вигляд
. Отже, рівняння площини, що проектує пряму, має вигляд 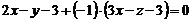 , або
, або 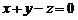 . Шукану проекцію можна визначити як лінію перетину двох площин – заданої і тієї, що проектує,
. Шукану проекцію можна визначити як лінію перетину двох площин – заданої і тієї, що проектує, 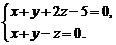 Звівши ці рівняння прямої до канонічного вигляду, одержимо
Звівши ці рівняння прямої до канонічного вигляду, одержимо 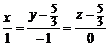 .
.
Date: 2015-07-23; view: 1749; Нарушение авторских прав