
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Різні види рівнянь прямої в просторі
|
|
Пряма в просторі
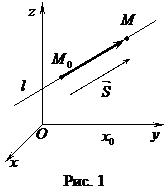 Нехай у просторі в прямокутній системі координат задана пряма
Нехай у просторі в прямокутній системі координат задана пряма 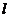 , її напрямний вектор
, її напрямний вектор 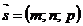 і точка
і точка 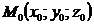 , що належить цій прямій. Візьмемо довільну точку на цій прямій
, що належить цій прямій. Візьмемо довільну точку на цій прямій 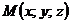 (рис. 1).
(рис. 1).
Як зазначалося в п. 9.2.1, векторне параметричне рівняння прямої як на площині, так і в просторі має вигляд (9.5):
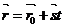 , (1)
, (1)
де 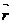 – радіус-вектор змінної точки М,
– радіус-вектор змінної точки М,  – радіус-вектор заданої точки М 0,
– радіус-вектор заданої точки М 0, 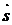 – ненульовий напрямний вектор прямої,
– ненульовий напрямний вектор прямої, 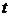 – параметр.
– параметр.
Аналогічно одержимо відповідно:
1) канонічні рівняння прямої в просторі 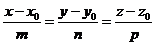 , (2)
, (2)
2) параметричні рівняння прямої в просторі 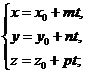 (3)
(3)
зокрема, ці рівняння можуть бути записані у вигляді 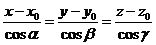 , (4)
, (4)
де 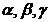 – кути, утворені прямою з координатними осями, причому напрямні косинуси обраховуються за формулами
– кути, утворені прямою з координатними осями, причому напрямні косинуси обраховуються за формулами
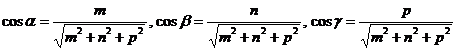 ; (5)
; (5)
3) рівняння прямої в просторі, яка проходить через дві задані точки 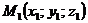 і
і 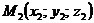
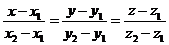 . (6)
. (6)
Розглянемо випадки розташування прямої у просторі, коли в рівняннях (2), (3), (6) одна або дві координати напрямного вектора дорівнюють нулю (ситуація, при якій 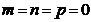 або
або 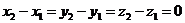 , неможлива, бо за означенням напрямний вектор ненульовий) у вигляді таблиці 1
, неможлива, бо за означенням напрямний вектор ненульовий) у вигляді таблиці 1
Приклад. 1. Скласти канонічне рівняння прямої, що проходить через точку 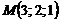 і перетинає вісь Ох під прямим кутом.
і перетинає вісь Ох під прямим кутом.
… Так як пряма перпендикулярна вісі Ох, то згідно з таблицею 1 рівняння цієї прямої матиме вигляд 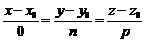 , де
, де  . Точка
. Точка 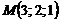 належить цій прямій, значить, її координати задовольняють рівняння цієї прямої, тобто
належить цій прямій, значить, її координати задовольняють рівняння цієї прямої, тобто 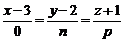 . Отже, шукане канонічне рівняння має вигляд
. Отже, шукане канонічне рівняння має вигляд 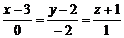 . †
. †
Таблиця 1
| Значення координат напрямного вектора | Вигляд рівняння | Розташування прямої в просторі |
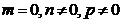
| 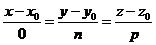
| Перпендикулярна вісі 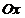 . .
|
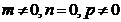
| 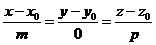
| Перпендикулярна вісі 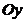 . .
|
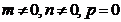
| 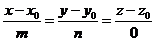
| Перпендикулярна вісі 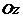 . .
|
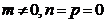
| 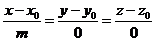
| Паралельна вісі 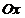 . .
|
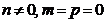
| 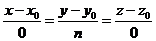
| Паралельна вісі 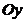 . .
|
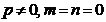
| 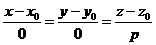
| Паралельна вісі 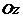 . .
|
Відомо, що дві непаралельні площини перетинаються по прямій лінії. Отже, система рівнянь двох площин П 1 і П 2
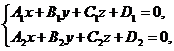 (7)
(7)
 нормальні вектори яких
нормальні вектори яких 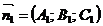 і
і 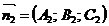 не колінеарні, визначає пряму лінію. Рівняння (7) називаються загальними рівняннями прямої в просторі.
не колінеарні, визначає пряму лінію. Рівняння (7) називаються загальними рівняннями прямої в просторі.
Приклад. 2. Побудувати пряму
 .
.
… Шукану пряму можна побудувати як лінію перетину площин. Для цього запишемо рівняння цих площин у відрізках на осях:
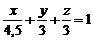 і
і 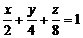 .
.
Побудувавши данні площини, одержимо шукану пряму (рис. 2). †
Виключивши по черзі з рівнянь (7) х і у, одержимо рівняння прямої, яка визначається площинами, що проектують її на координатні площини Охz і Оуz:
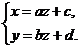 (8)
(8)
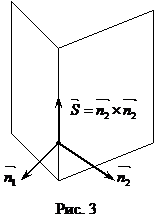 Щоб від загальних рівнянь (7) перейти до канонічних рівнянь (3), потрібно знайти точку
Щоб від загальних рівнянь (7) перейти до канонічних рівнянь (3), потрібно знайти точку 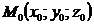 , що належить цій прямій, та її напрямний вектор
, що належить цій прямій, та її напрямний вектор 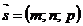 . Для знаходження точки М 0 одну з її координат, наприклад,
. Для знаходження точки М 0 одну з її координат, наприклад, 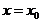 беруть довільною, а дві інші визначають із системи
беруть довільною, а дві інші визначають із системи
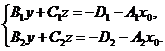
Ця система матиме розв’язок за умови 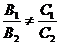 . Якщо ця умова порушується, то в системі (7) довільне значення надають змінній у або змінній z. Для знаходження напрямного вектора
. Якщо ця умова порушується, то в системі (7) довільне значення надають змінній у або змінній z. Для знаходження напрямного вектора 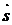 , врахуємо, що нормальні вектори
, врахуємо, що нормальні вектори 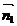 і
і 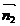 даних площин перпендикулярні до прямої (рис. 3). Тому за вектор
даних площин перпендикулярні до прямої (рис. 3). Тому за вектор 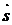 можна взяти векторний добуток нормальних векторів:
можна взяти векторний добуток нормальних векторів:
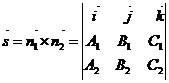 . (9)
. (9)
Приклад. 3. Звести до канонічного вигляду загальні рівняння прямої
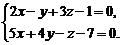
… І спосіб. Виключивши спочатку у, а потім z, одержимо аналогічно (8) 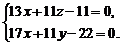 Якщо розв’язати кожне рівняння системи відносно х, то отримаємо
Якщо розв’язати кожне рівняння системи відносно х, то отримаємо 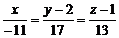 .
.
ІІ спосіб. Знайдемо за формулою (9), де 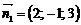 і
і 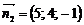 , напрямний вектор шуканої прямої
, напрямний вектор шуканої прямої
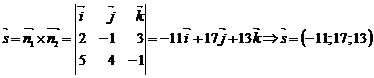 .
.
Поклавши тепер в початковій системі 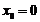 , отримаємо систему
, отримаємо систему  . Розв’язуючи цю систему, знайдемо ординату та аплікату точки, яка належить даній прямій,
. Розв’язуючи цю систему, знайдемо ординату та аплікату точки, яка належить даній прямій, 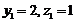 . Отже, дана пряма має канонічні рівняння
. Отже, дана пряма має канонічні рівняння 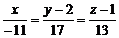 . †
. †
Date: 2015-07-23; view: 2492; Нарушение авторских прав