
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Блоковые статистики→по столбцам→Среднее
|
|
В результате под столбцам буду вычислены средние относительные ошибки, которые надо умножить на 100%.
Для МНК- модели MAPE= 34,56%
Для ОМНК-модели MAPE=27,01%
Скорректированная модель (**) по всем параметрам лучше, чем полученная в п.3.
в. Отсутствие автокорреляции
Отсутствие автокорреляции остатков подтверждается статистикой Дарбина-Уотсона.
Окно Результаты множественной регрессии → вкладка Остатки/Предсказанные/Наблюдаемые значения → кнопка Анализ остатков.
В окне Анализ остатков → вкладка Дополнительно → кнопка Статистика Дарбина-Уотсона

По таблицам находим значения верхней и нижней границ статистики DW
При n=52 и p=2 (два фактора в уравнении) dU=1,59 и dL=1,5. Так как DW=1,711> dU, то автокорреляция остатков отсутствует.
г. Нормальный закон распределения остатков;
Построить гистограмму остатков и подтвердить нормальность их распределения можно:
1) окно Анализ остатков → вкладка Остатки → кнопка Гистограмма остатков

2) использовать Графики → Гистограмма

Критические значение критерия Колмогорова-Смирнова при α=0.05 и числе наблюдений n=52 составляет Dкр = 0.188. Так как вычисленное значение статистики D=0,1366<Dкр, то гипотеза о нормальном распределении остатков принимается.
3) использовать вероятностный график остатков: окно Анализ остатков → вкладка Вероятностные графики → кнопка Нормальный
Это график остатков, построенный на специальной «вероятностной бумаге», сетка которой масштабирована так, что нормальные данные на этой сетке ложатся на прямую. На рисунке эта прямая изображена сплошной линией, а остатки – в виде точек. По рисунку видно, что точки расположены очень близко к прямой. Это еще раз подтверждает нормальность распределения остатков в последней (ОМНК) модели.

Задание 4. Построение нелинейной формы с полным набором факторов и оценку качества построенной модели
(форма модели выбирается по правилу:
0 - полулогарифмическая модель;
1 - гиперболическая модель;
2 - мультипликативная модель;
3 - экспоненциальная модель,
где 0, 1, 2, 3 - остаток от деления номера варианта на 4);
При анализе зависимости результативного признака Yот всех факторов (Задание 1, рис.13) выдвинуто предположение о линейной зависимости от факторов X1, X3, X4 и логарифмической зависимости (или параболической) от факторов X2 и X5.
То есть предполагаемая форма нелинейной зависимости:

Это смешанная (не полулогарифмическая и не мультипликативная) модель.
Ее мы построим позже.
По заданию выберем наиболее сложную для анализа - мультипликативную модель:
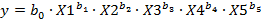
Преобразуем ее к линейному виду (прологарифмируем):
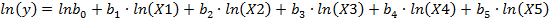
Введя обозначения 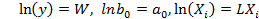 , получим уравнение линейной регрессии:
, получим уравнение линейной регрессии:
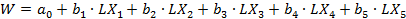
Для расчета параметров этого уравнения введем в основную таблицу новые переменные – логарифмы исходных данных. Для этого, во-первых, добавим в таблице переменные. Для этого выполним команду Переменные→Добавить. В появившемся окне укажем, что добавляется 10 переменных после переменной MAPE (рис. 21) → ОК
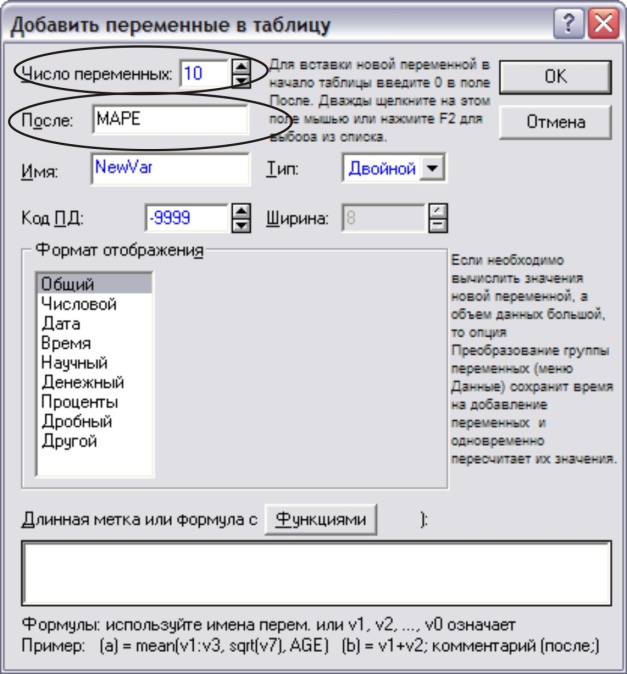
Рис. 21.
Выполним команду Переменные → Все спецификации. В появившемся окне введем имена переменных и формулы их вычисления (рис. 22)
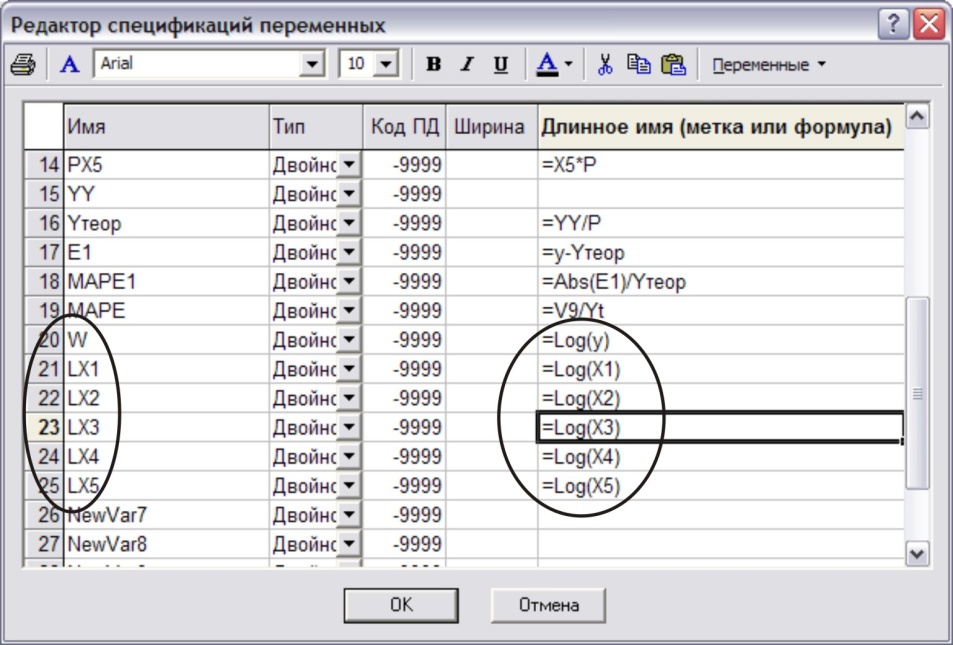
Рис. 22
В результате в исходной таблице появятся данные для построения нелинейной модели рис. 23 (фрагмент таблицы)
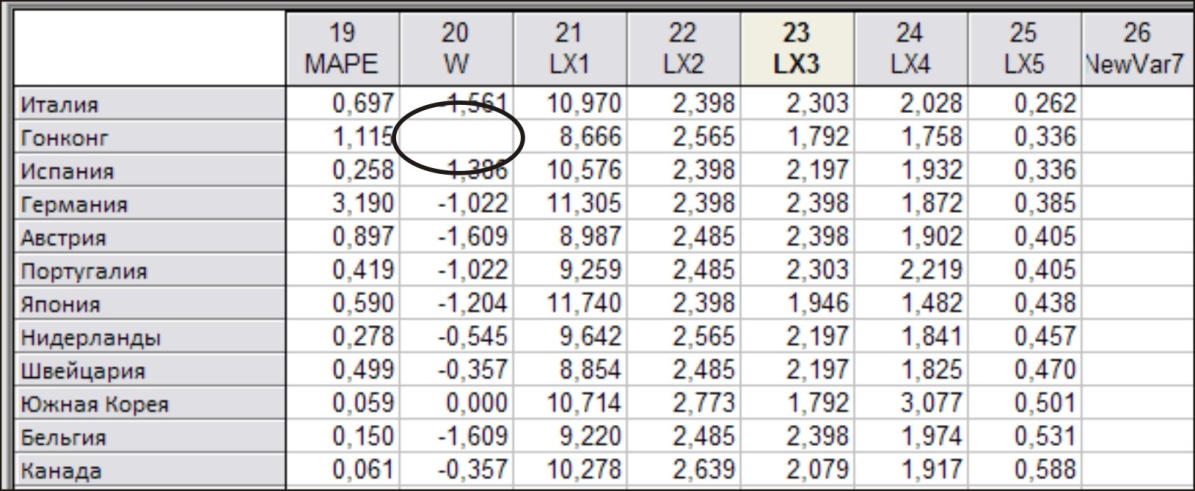
Рис. 23.
Обратите внимание, что в таблице появились пропущенные значения. Это связано с тем значение переменной Y для Гонконга - отрицательное число, логарифм которого вычислен быть не может. При выполнении регрессионного анализа такие данные будут пропускаться.
Выполним команду Анализ→Множественная регрессия. В появившемся окне нажать кнопку Переменные. В окне «Списки зависимых и независимых переменных» слева указать зависимую переменную W, а справа – все остальные факторные переменные LX1, LX2, LX3, LX4, LX5. → ОК
Для анализа построенной модели выведем результаты – кнопка Итоговая таблица регрессии.
В результате Statistica выдает две таблицы: Итоговые статистики и Итоги регрессии


В целом уравнение регрессии значимо, коэффициент детерминации достаточно высокий, но в уравнении присутствуют незначимое параметры – коэффициенты при переменных LX1 и LX5. Нажмет кнопку Отмена. В результате попадем в стартовое окно регрессии, где необходимо выставить флажок у опции Пошаговая или гребневая регрессия (см. Задание 3, рис. 15)
Запустим процедуру пошаговой регрессии с исключением (см. Задание 3, рис. 16).
В окне Результаты множественной регрессии → выберем вкладку Дополнительно нажмем кнопки → Итогоавя таблица регрессии, Дисперсионный анализ.
В результате получим несколько таблиц
Зависимая перемен.: W
Множест. R:,921637198
Множест. R-квадр.:,849415124
Скоррект.R-Квадр.:,843140754
Число наблюд.: 51
F (2, 48) = 135,3786 p <0,000000
Стандартная ошибка оценки:,397692340



Обратите внимание, что число наблюдений, по которым строилось уравнение регрессии, уменьшилось на единицу. Соответственно, и число степеней свободы, используемые для расчета критических значений tкр и Fкр, изменится.
Замечание: Характеристики R2=0,849, Fв=135,38, Стандартная ошибка оценки=0,39769 относятся к регрессионной модели для объясняемой переменной W=ln y.
Нам же необходимо определить эти характеристики для переменной Y.
Уравнение регрессии, полученное при пошаговой процедуре исключения выглядит следующим образом:
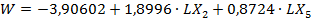
Потенцируя это уравнение, получим:
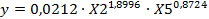 , где
, где 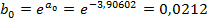
Используя эту формулу, рассчитаем теоретические значения переменной Y по нелинейной модели. Для этого в основной таблице введем новую переменную YY и определим для ее вычисления вышеприведенную формулу (рис. 24).
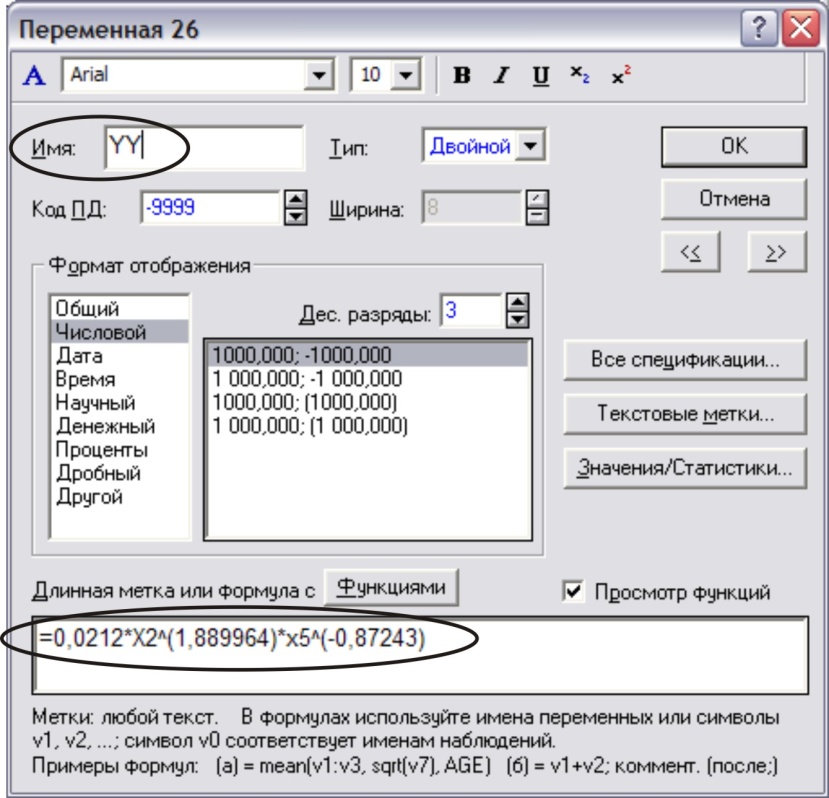
Рис. 24.
Теперь мы можем рассчитать основные характеристики уравнения регрессии. Для этого необходимо вычислить остатки модели, сумму квадратов остатков, коэффициент детерминации. Эти вычисления проще сделать в Excel (приведен фрагмент и вычисленные характеристики).
| YY | E | E^2 |
| 1,567 | -1,357 | 1,842 |
| 2,014 | -2,104 | 4,429 |
| 1,469 | -1,219 | 1,486 |
| 4,776 | -3,146 | 9,900 |
| 3,918 | -0,718 | 0,516 |
| 5,615 | -2,815 | 7,923 |
| 5,296 | -2,196 | 4,824 |
| 5,656 | -2,846 | 8,100 |
| Сумма | 150,260 | |
| Se | 0,165306 | |
| D(y) | 1,092 | |
| R2 | 0,848676 |
Определяем с помощью вероятностного калькулятора
Fкр = F(0,95; 2; 51-2-1)=F(0,95; 2; 48)=3,190727,
tкр=t(0,95; 51– 2 – 1)=t(0,95; 48)=2,010635.
Задание 5. Расчет коэффициентов эластичности для каждой модели;'
Задание 6. проверку предпосылок использования метода наименьших квадратов:
а. Случайность остатков;
б. Постоянство их дисперсии (тест Гольфельда-Квандта);
в. Отсутствие автокорреляции (статистика Дарбина-Уотсона);
г. Нормальный закон распределения остатков;
Задание 7. В случае невыполнения предпосылок МНК предложите вариант коррекции модели.
Задание 8. Сравните построенные модели. Выберите лучшую. Выбор обоснуйте.
Задание 9. Выполните расчет прогнозного значения результата, предполагая, что прогнозные значения факторов составят 104,2% от их среднего уровня.
Date: 2015-07-23; view: 374; Нарушение авторских прав