
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Выполним задания 5, 6 и 7 для построенной линейной модели множественной регрессии
|
|
Задание 5. Расчет коэффициентов эластичности. Вычислим средние коэффициенты эластичности:
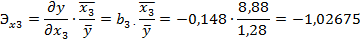
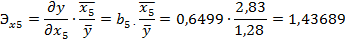
Коэффициент эластичности при факторе X3 показывает, что при изменении смертности на 1% от среднего уровня прирост населения изменится в обратную сторону на 1,03% от своего среднего уровня при фиксированном среднем числе детей в семье.
Коэффициент элестичности при факторе X5 показывает, что при изменении среднего числа детей в семье на 1% от среднего уровня прирост населения изменится в ту же сторону на 1,44% от своего среднего уровня при фиксированном уровне смертности.
Сравнивая эти коэффициенты между собой, можно сделать вывод, что среднее число детей в семье более сильно влияет на прирост населения, чем уровень смертности.
Задание 6. Проверка предпосылок использования метода наименьших квадратов:
Для исследования свойств остатков в диалоговом окне Результаты множественной регрессии →вкладка Остатки/Предсказанные/Наблюдаемые значения → кнопка Анализ остатков
а. Случайность остатков;
Для проверки случайности остатков обычно используются специальные тесты (например, тест серий). Мы убедимся в случайности остатков, построив диаграмму рассеяния, и подтвердив отсутствие тенденции.
Для построения диаграммы в диалоговом окне Анализ остатков выбираем→ вкладку Диаграммы рассеяния и кнопку Предсказанные и остатки

В результате получим диаграмму, анализ которой показывает, что зависимость е=е(y(x)) не содержит тенденции и точки располагаются вблизи оси абсцисс. Следовательно, предпосылка о случайности остатков выполняется
б. Постоянство дисперсии остатков (гомоскедастичность) (тест Гольфельда-Квандта);

В окне Анализ остатков → перейдем на вкладку Дополнительно → выберем кнопку Остатки и предсказанные. В результате появится таблица, два столбца из которой – Предск. значение и Остатки скопируем в буфер обмена (рис. 18)
Перейдем в таблицу с исходными данными. Добавим новые переменные. Для этого выполним команду Переменные → Добавить. В появившемся диалоговом окне укажем, что надо добавить 12 переменных после переменной Y
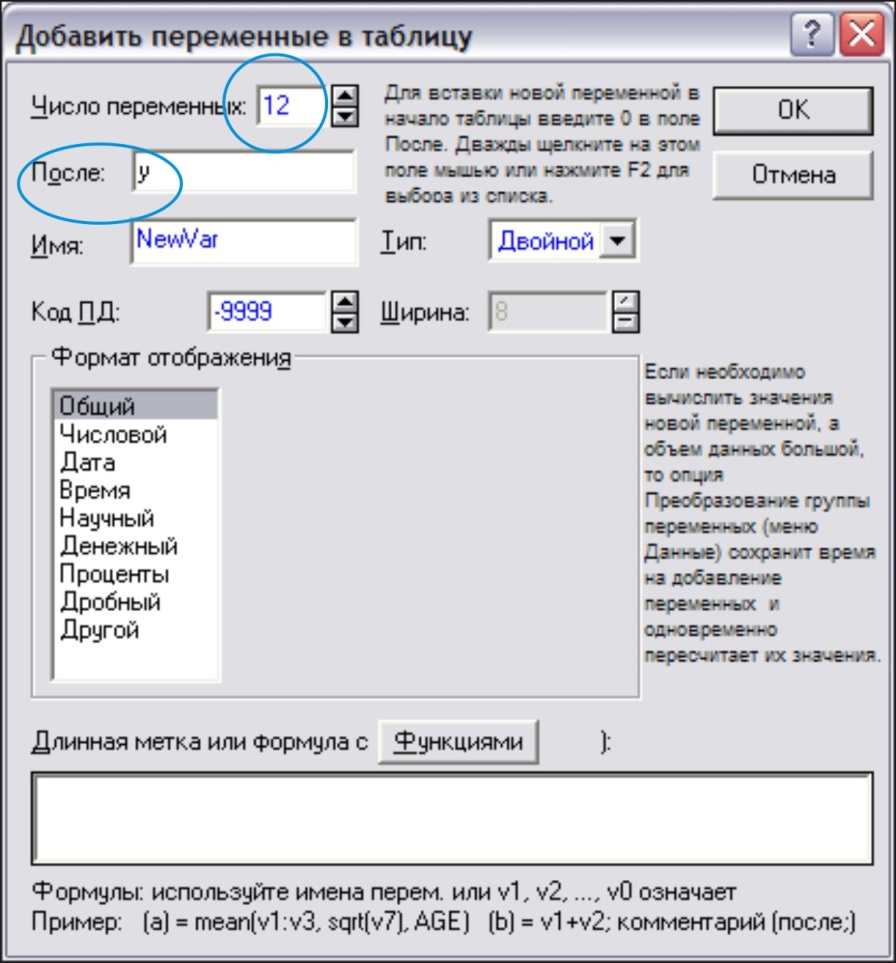
Рис. 18.
Далее необходимо вставить из буфера данные и переименовать переменные (например, Yt – для рассчитанных по модели значений Y, и E – для остатков). Для переименования достаточно дважды щелкнуть на имени переменной и в открывшемся окне прописать имя переменной.
Для проведения теста Гольфельда-Квандта разобъем все данные на 3 части, исключив средние 18 наблюдений. В первой группе будет 17 наблюдений с номерами с 1 по 17, во второй группе также 17 наблюдений с номерами с 36 по 52.
Рассмотрим отдельно каждый из оставшихся в модели фактор.
Упорядочить объем нашей совокупности по фактору X3 (Сортировка по
возрастанию): щелкнуть на имени переменной и выбрать кнопку сортировки 
Выйти из окна Анализ остатков – кнопка Отмена
Выйти из окна Определение модели – кнопка Отмена
В стартовом окне Множественная регрессия нажать кнопку Переменные
Выбрать в качестве факторов оставшиеся при проведении пошаговой регрессии переменные (у нас X3 и X5)
В стартовом окне Множественная регрессия нажать кнопку Select cases Y (выбор наблюдений) (рис. 19)
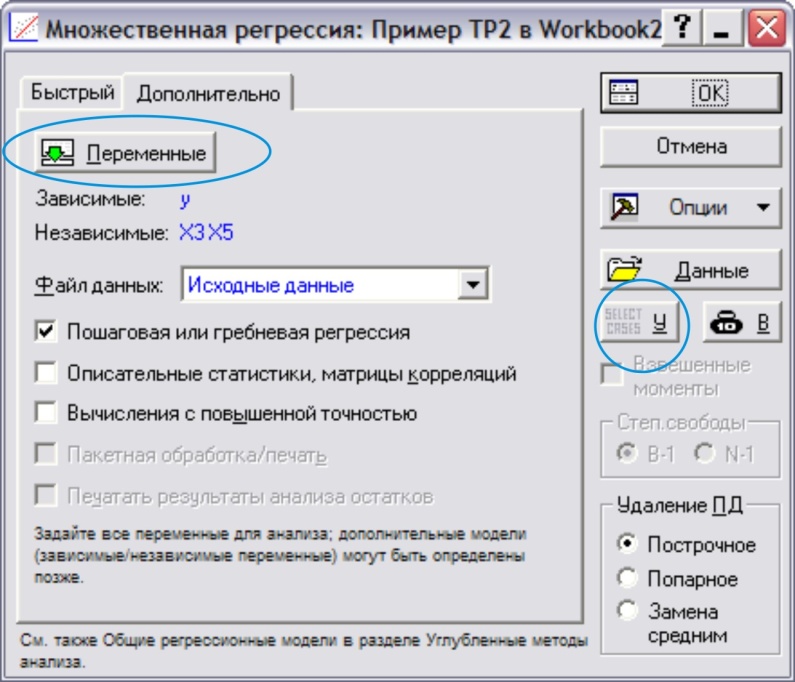
Рис. 19.
В появившемся окне Условия выбора наблюдений Анализа выставить необходимые флажки и включить опции, указать номера наблюдений с 1 по 17 (рис. 20). ОК

Рис. 20
В стартовом окне Множественная регрессия нажать кнопку ОК
В окне Определение модели нажать кнопку ОК
В окне Результаты множественной регрессии перейти на вкладку Дополнительно и нажать кнопку Дисперсионный анализ
В результате получим таблицу Дисперсионного анализа

Для прведения теста Гольфельда-Квандта нам нужна Остаточная сумма квадратов. В этой таблице она находится в строке Остатки столбца Сумма квадратов:
SS1=1,45247.
Вернемся в стартовое окно Множественная регрессия. С помощью кнопки Select cases Y
Выберем теперь наблюдения с номерами с 36 по 52. Далле – как и для группы наблюдений с минимальными значениями X3.

Сумма квадратов остатков для выбранных наблюдений:
SS2=1,90467
Вычислим F-статистику теста Гольфельда-Квындта: 
Найдем критическое значение статистики:
Fкр=F(0,95; n1-p-1; n2-p-1)=F(0,95; 17-2-1; 17-2-1)=F(0,95;14;14)= 2,484
Так как Fв<Fкр, то гипотеза о гомоскедастичности остатков (независимость остатков от величины фактора X3) принимается.
Проведем такую же проверку по фактору X5
В результате получим:
УСЛОВИЯ ВЫБОРА НАБЛЮДЕНИЙ:
Включить наблюдение с номером: 1:17

УСЛОВИЯ ВЫБОРА НАБЛЮДЕНИЙ:
Включить наблюдение с номером: 36:52

Вычислим F-статистику теста Гольфельда-Квындта: 
Так как Fв>Fкр, то гипотеза о гомоскедастичности остатков (независимость остатков от величины фактора X5) отклоняется.
Не выполняется одна из предпосылок МНК. Необходима коррекция модели – применение обобщенного метода наименьших квадратов (ОМНК). Для этого необходимо знать аналитический вид зависимости дисперсии остатков от переменной X5.
Воспользуемся тестом Глейзера. Причем, поиск зависимости |e| от переменной X5 не дал положительных орезультатов. Поэтому было решено использовать тест Уайта. В результате было получено уравнение регрессии |e| на факторы X3 и X5.
Нахождение коэффициентов модели осуществлялось в модуле Нелинейное оценивание (хотя модель получилась линейной)

|e|= 0,4066-0,0412*X3 + 0,07237*X5; R2= 0,249.
Предсказанные значения остатков (см. таблицу ниже) необходимо скопировать в таблицу с исходными данными.

Теоретически рассчитанные остатки (только-что вставленные) назовем S. Используя их вычислим «веса» для всех переменных модели. Для этого введем переменную P:
Pi=1/Si
Введем новые переменные PY=Y*P; PX3=X3*P; PX5=X5*P
Будем строить «взвешенное» уравнение регрессии:
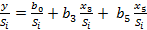 (*)
(*)
без свободного члена – он заменяется весовым коэффициентом Pi=1/Si.


Так как все члены уравнения (*) делятся для каждого наблюдения на одно и то же число, то уравнение можно записать в виде:
Y= 0,808-0,1451*X3+0,6194*X5. (**)
При сравнении модели из п.3 с данной, видим, что коэффициент детерминации у последней модели выше, дисперсии коэффициентов регрессии – ниже.

Предсказанные значения скопируем в исходную таблицу – назовем YY.
Для сравнения исходной модели, полученной МНК, и последней модели (ОМНК) вычислим среднюю относительную ошибку аппроксимации MAPE:
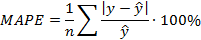
Для этого введем в исходную таблицу дополнительные столбцы:
Yтеор=YY/P – исключение «веса» из теоретически рассчитанной переменной PY
E1=y-Yтеор – ошибка последней модели
MAPE1=Abs(E1)/Yтеор - по последней (ОМНК) модели;
МAPE=Abs(E)/Yt – по модели, построенной в Задании 3.
После вычислений выделить последние два столбца (только числа), нажать ПРАВОЙ кнопкой мыши, в выпадающем меню выбрать
Date: 2015-07-23; view: 425; Нарушение авторских прав