
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Выполнение типового расчета № 2
|
|
Настройка приложения
Рекомендуется включить опцию составления отчета. Это упростит в дальнейшем составление отчета по типовому расчету. Для этого необходимо выполнить команду
Сервис (Tools) → Параметры(??????).
В отрывшемся окне выбрать вкладку Диспетчер вывода (Output manager) (рис. Г).
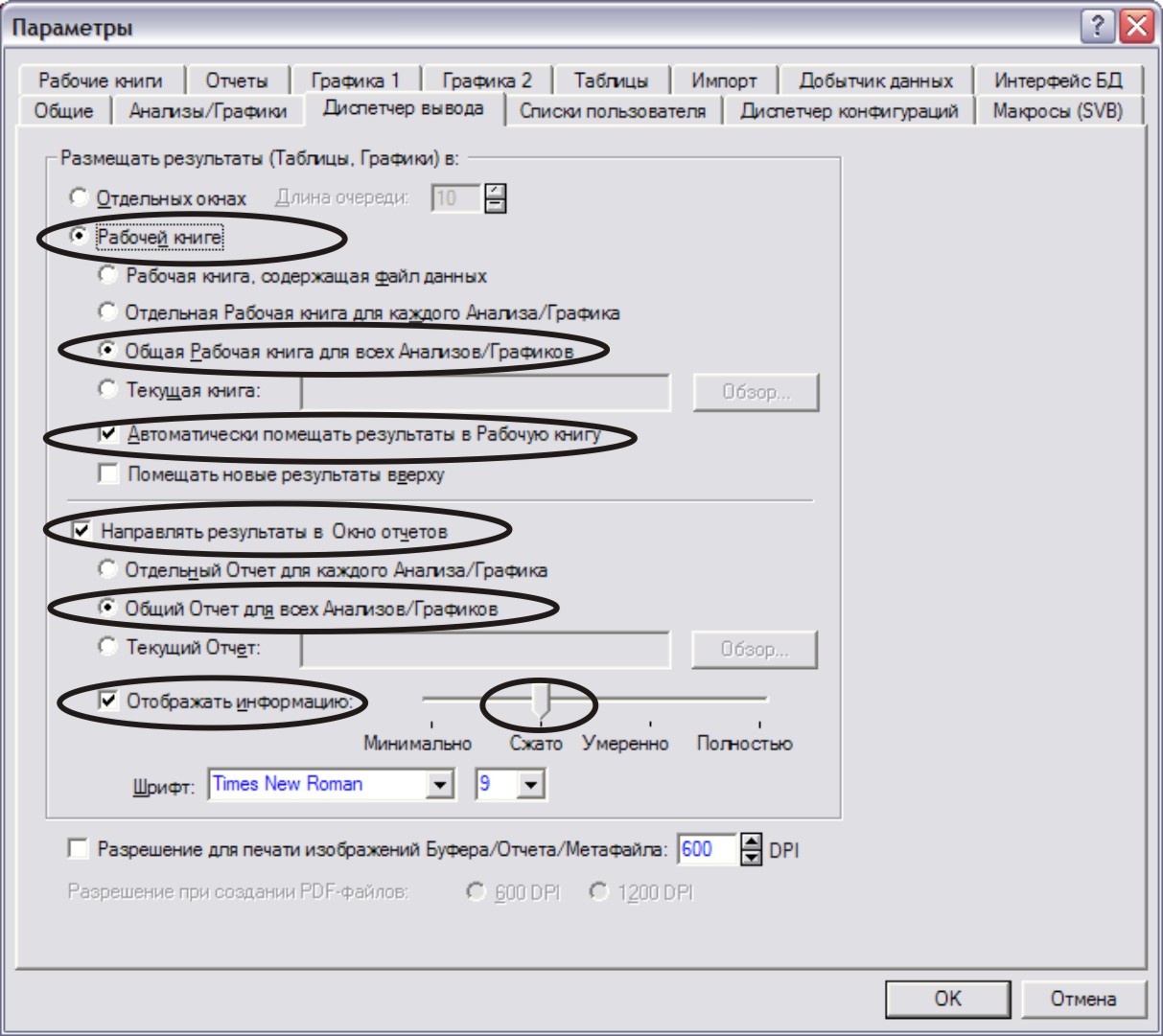
Рис. Г.
Выставить флажки и выбрать опции как на рисунке.
Далее выбрать вкладку Отчет (Report) (рис. Д).
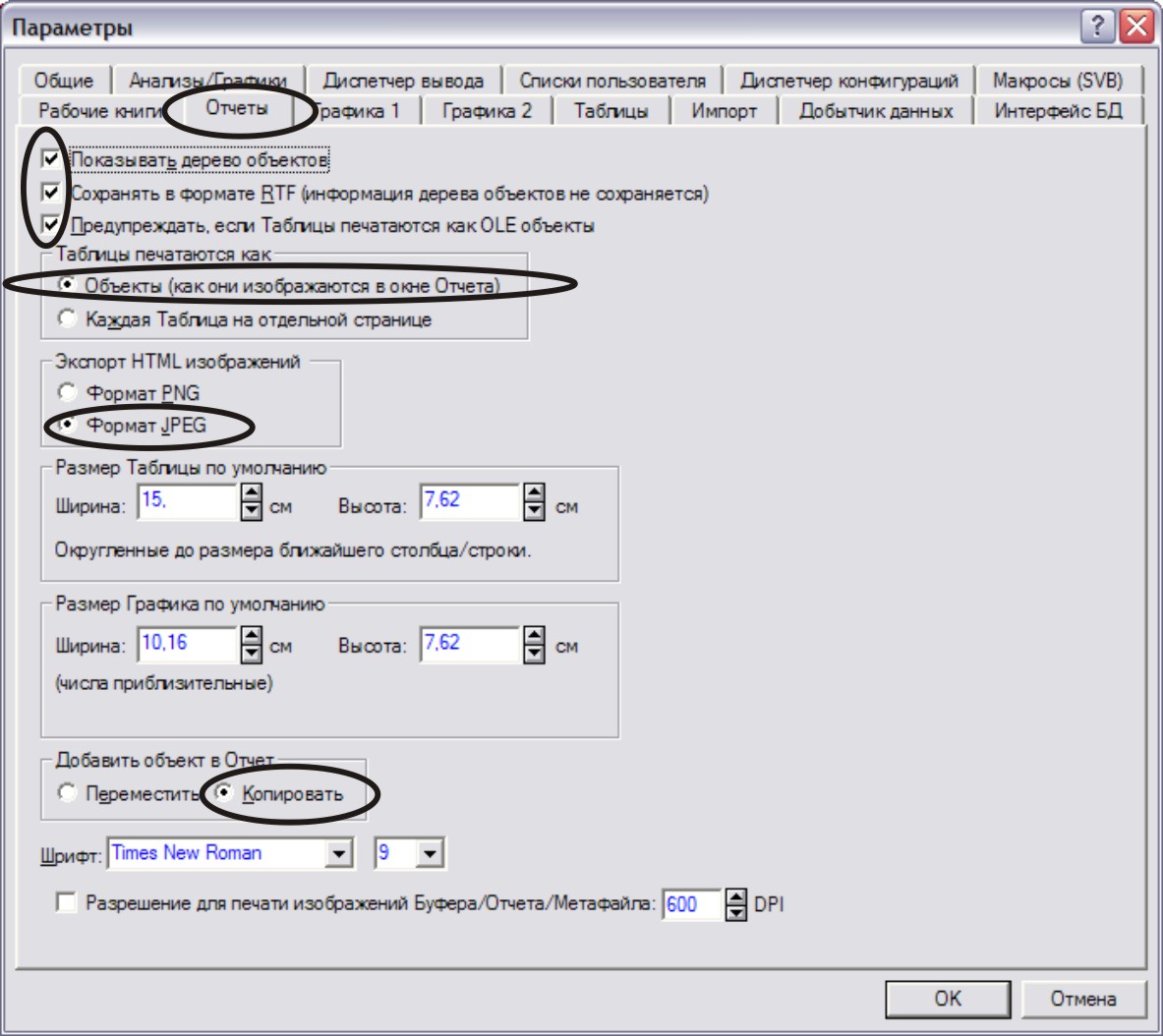
Рис. Д.
Выставить флажки и выбрать опции как на рисунке.
В результате все таблицы и графики, котрые Вы будете получать в результате решения задачи будут отражаться в отчете, который по окончании работы следует сохранить (файл с расширением rtf).
Перед сохранением просмотрите отчет, не выходя из программы Statistica. Если некоторые из таблиц не полностью отражаются (обрезаны), то пока Вы находитесь в программе Statistica, у Вас есть возможность растянутьтаблицы и графики так, чтобы отражались все необходимые данные. После сохранения, окрыв отчет в Word, вы не будете иметь такой возможности.
Полученный таким образом отчет, после вставки Ваших комментариев и некоторых дополнительных вычислений (можно от руки), после удаления ненужных комментариев программы Statistica, сдается преподавателю для проверки.
Выполнение типового расчета № 2
Для примера рассмотрим данные:
| Обозначения признаков | |
| X1 | численность населения (в тыс. чел) |
| X2 | рождаемость (на 1000 чел.) |
| X3 | смертность (на 1000 чел.) |
| X4 | младенческая смертность - число детей, умерших в возрасте до 1 г. (на 1000 чел.) |
| X5 | среднее число детей в семье |
| Y | прирост населения (% в год) |
| № | Страна | X1 | X2 | X3 | X4 | X5 | y |
| Австралия | 7,3 | 1,9 | 1,38 | ||||
| Австрия | 6,7 | 1,5 | 0,2 | ||||
| Аргентина | 25,6 | 2,8 | 1,3 | ||||
| Бангладеш | 4,7 | 2,4 | |||||
| Беларусь | 1,88 | 0,32 | |||||
| Бельгия | 7,2 | 1,7 | 0,2 | ||||
| Бразилия | 2,7 | 1,28 | |||||
| Буркина-Фасо | 6,94 | 2,81 | |||||
| Великобритания | 7,2 | 1,83 | 0,2 | ||||
| Вьетнам | 3,33 | 1,78 | |||||
| Гаити | 5,94 | 1,63 | |||||
| Германия | 6,5 | 1,47 | 0,36 | ||||
| Гондурас | 4,9 | 2,73 | |||||
| Гонконг | 5,8 | 1,4 | -0,09 | ||||
| Египет | 76,4 | 3,77 | 1,95 | ||||
| Замбия | 6,68 | 2,8 | |||||
| Индия | 4,48 | 1,9 | |||||
| Ирландия | 7,4 | 1,99 | 0,3 | ||||
| Испания | 6,9 | 1,4 | 0,25 | ||||
| Италия | 7,6 | 1,3 | 0,21 | ||||
| Канада | 6,8 | 1,8 | 0,7 | ||||
| Китай | 1,84 | 1,1 | |||||
| Колумбия | 2,47 | ||||||
| Коста-Рика | 3,1 | 2,3 | |||||
| Куба | 10,2 | 1,9 | 0,95 | ||||
| Малайзия | 25,6 | 3,51 | 2,3 | ||||
| Марокко | 3,83 | 2,12 | |||||
| Мексика | 3,2 | 1,9 | |||||
| Нидерланды | 6,3 | 1,58 | 0,58 | ||||
| Новая Зеландия | 8,9 | 2,03 | 0,57 | ||||
| Норвегия | 6,3 | 0,4 | |||||
| ОАЭ | 4,5 | 4,8 | |||||
| Польша | 13,8 | 1,94 | 0,3 | ||||
| Португалия | 9,2 | 1,5 | 0,36 | ||||
| Россия | 1,83 | 0,2 | |||||
| Саудовская Аравия | 6,67 | 3,2 | |||||
| Северная Корея | 27,7 | 2,4 | 1,83 | ||||
| Сингапур | 5,7 | 1,8 | 1,2 | ||||
| США | 8,11 | 2,06 | 0,99 | ||||
| Тайланд | 2,1 | 1,4 | |||||
| Турция | 3,21 | 1,02 | |||||
| Украина | 20,7 | 1,82 | 0,05 | ||||
| Филиппины | 3,35 | 1,92 | |||||
| Финляндия | 5,3 | 1,8 | 0,3 | ||||
| Франция | 6,7 | 1,8 | 0,47 | ||||
| Чили | 14,6 | 2,5 | 1,7 | ||||
| Швейцария | 6,2 | 1,6 | 0,7 | ||||
| Швеция | 5,7 | 2,1 | 0,52 | ||||
| Эфиопия | 6,81 | 3,1 | |||||
| ЮАР | 47,1 | 4,37 | 2,6 | ||||
| Южная Корея | 21,7 | 1,65 | |||||
| Япония | 4,4 | 1,55 | 0,3 |
Для набора экономических или финансовых показателей выполнить:
Задание 1. Cпецификацию множественной зависимости. В ходе спецификации
определить:
- мультиколлинеарность факторов;
- набор информативных факторов;
- коэффициенты частной корреляции;
- коэффициент детерминации;
Для выбора формы модели и анализа факторов, которые необходимо включить в модель, необходимо оценить корреляционные связи всех факторов. Это позволит выявить мультиколлинеарные факторы.
Сначала определим основные статистические показатели переменных. Для этого в программе Statistica необходимо выполнить команду: Анализ→Основные статистики и таблицы→Описательные статистики→ ОК
В диалоговом окне (рис. 1) нажать на кнопку Переменные и в появившемся окне (рис. 2) выбрать все переменные → ОК
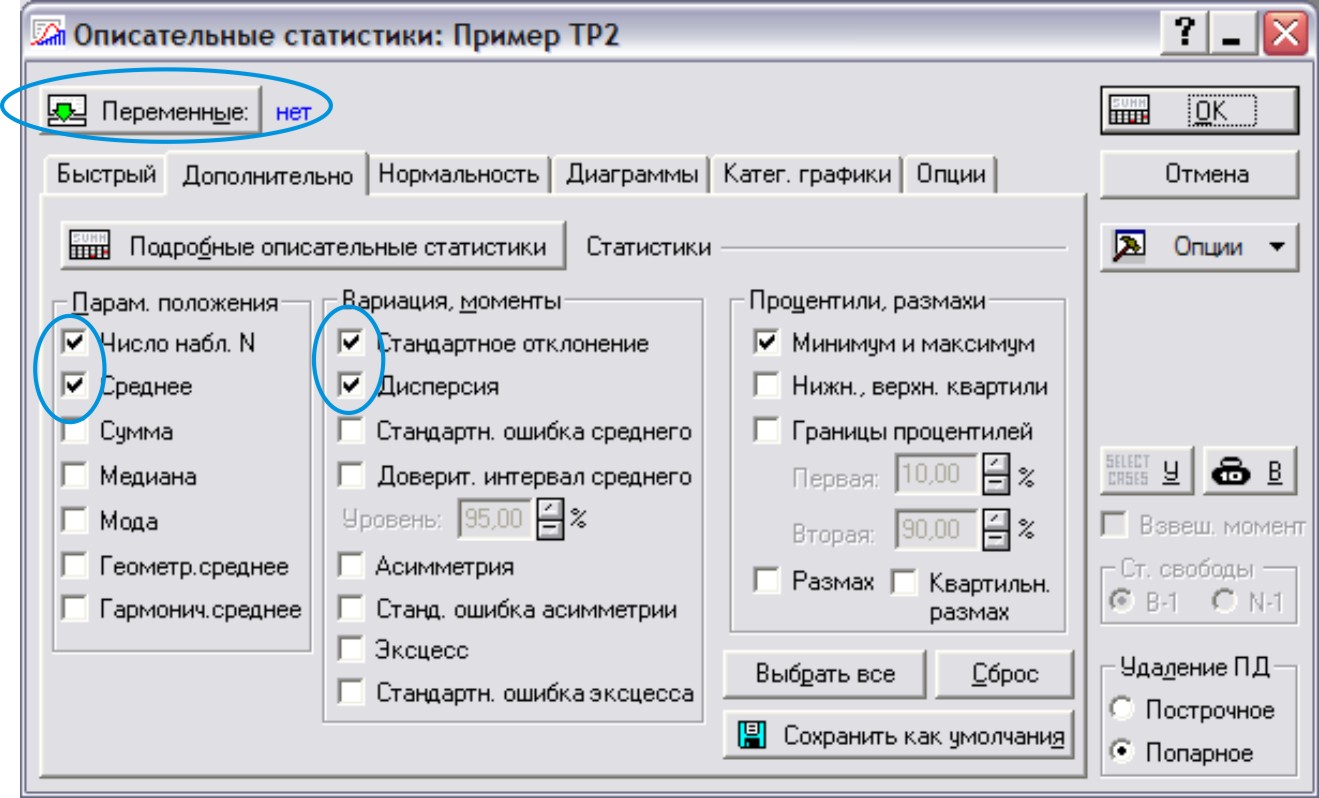
Рис.1
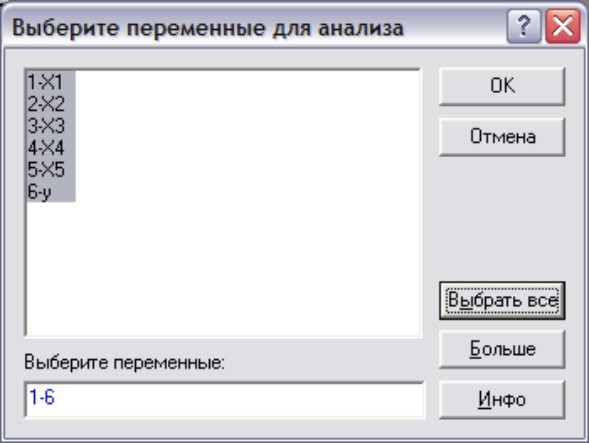
Рис.2
Вернулись в стартовое окно. В нем необходимо отметить основные статистические характеристики: Число наблюдений, Среднее, Стандартное отклонение, Дисперсия.(рис.1) → ОК
В результате появится таблица, содержащая основные статистические характеристики переменных

Для вычисления парных и частных корреляций необходимо включить другой тип анализа: Анализ → Основные статистики и таблицы→ Парные и частные корреляции→ ОК
Рис.3
В появившемся окне (рис. 4) нажать кнопку Квадратная матрица, в диалоговом окне выбора переменных нажать кнопку Выбрать все или выделить все переменные → ОК.

Рис.4.
Вернулись в стартовое окно. Нажимаем кнопку Матрица парных корреляций. В результате получаем таблицу:

Значения парных корреляций показывают тесную связь результативного признака Y - прирост населения (% в год) – с признаками (последняя строка или последний столбец таблицы:
X2 - рождаемость (на 1000 чел.)
X4 - младенческая смертность - число детей, умерших в возрасте до 1 г. (на 1000 чел.)
X5 - среднее число детей в семье
ryx2=0,85; ryx4=0,62; ryx5=0,82
Программа Statistica выделяет значимые на 95%-ном уровне корреляции красным цветом.
«Вручную» значимость корреляций можно подтвердить проверкой гипотезы:
H0: r=0
H1: r≠0 с помощью статистики 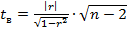 , которая при выполнении нулевой гипотезы имеет распределение Стьюдента с k=(n-2) степенями свободы.
, которая при выполнении нулевой гипотезы имеет распределение Стьюдента с k=(n-2) степенями свободы.
Для нашего примера n=52, тогда k=52-2=50.
Критическое значение показателя 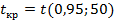 может быть вычислено с помищью вероятностного калькулятора в программе Statistica:
может быть вычислено с помищью вероятностного калькулятора в программе Statistica:
Анализ → Вероятностный калькулятор → Распределения (рис. 5)
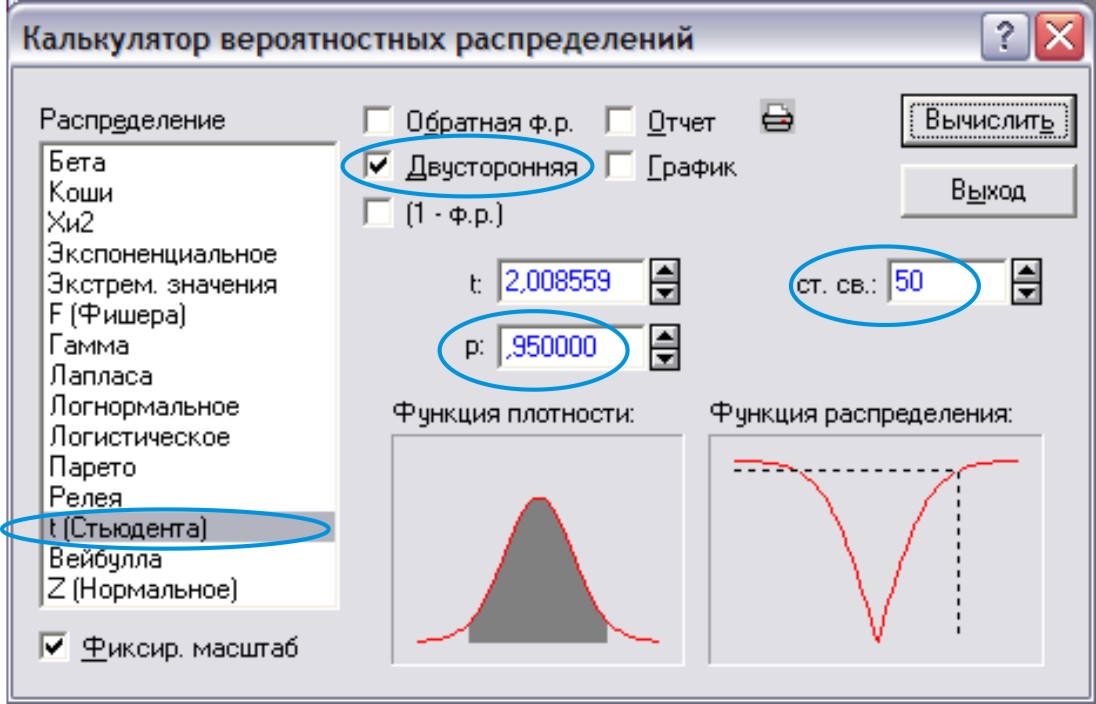
Рис.5
После ввода всех необходимых параметров нажать кнопку Вычислить.
Критическое значение 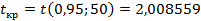
Выборочные t -статистики, рассчитанные для парных коэффициентов корреляции (вычислены во вспомогательном файле MS Excel)
| Значение | t-статистика | t кр | Вывод | ||
| ryx1 | 0,010 | 0,070906752 | < | 2,009 | не значим |
| ryx2 | 0,851 | 11,46396252 | > | 2,009 | значим |
| ryx3 | -0,140 | 0,997809759 | < | 2,009 | не значим |
| ryx4 | 0,615 | 5,518044665 | > | 2,009 | значим |
| ryx5 | 0,820 | 10,13594613 | > | 2,009 | значим |
Оценка парных коэффициентов корреляции между факторами указывает на сильную корреляционную связь переменных X2 и X4 (rx2x4=0,87), X2 и X5 (rx2x5=0,97), X4 и X5 (rx4x5=0,85). Значимой также является корреляционная связь между переменными X3 и X4 (rx3x4=0,46). Анализируя матрицу корреляций можем отметить, что переменная X1 слабо связана как с остальными факторами, так и с результативным признаком. Скорее всего, в уравнении регрессии она не войдет.

Наличие мультиколлинеарности подтверждается также вычислением определителя матрицы корреляций для факторов X1 – X5: Δ=0,0063 (функция МОПРЕД(массив) Excel).
Близкое к нулю значение определителя матрицы корреляций говорит о мультиколлинеарности факторов. Это означает, что при пошаговой процедуре регрессии, какие-то из факторов X2, X4 и X5 будут исключены, как дублирующие.
Более тщательный анализ связи переменных можно провести, вычисляя частные коэффициенты корреляции. Они показывают чистую связь двух признаков, исключая опосредованное влияние других переменных.
В программе Statistica частные коэффициетны корреляции вычисляются с помощью того же модуля Парные и частные корреляции.
Теперь в основном окне модуля необходимо выбрать кнопку Прямоугольная матрица, и в появившемся окне (рис. 6, 7):
- в левой части выбрать переменные, для которых вычисляется частный коэффициент корреляции;
-в правой части – указать фиксируемые (исключаемые из рассмотрения) прерменные.
ОК.
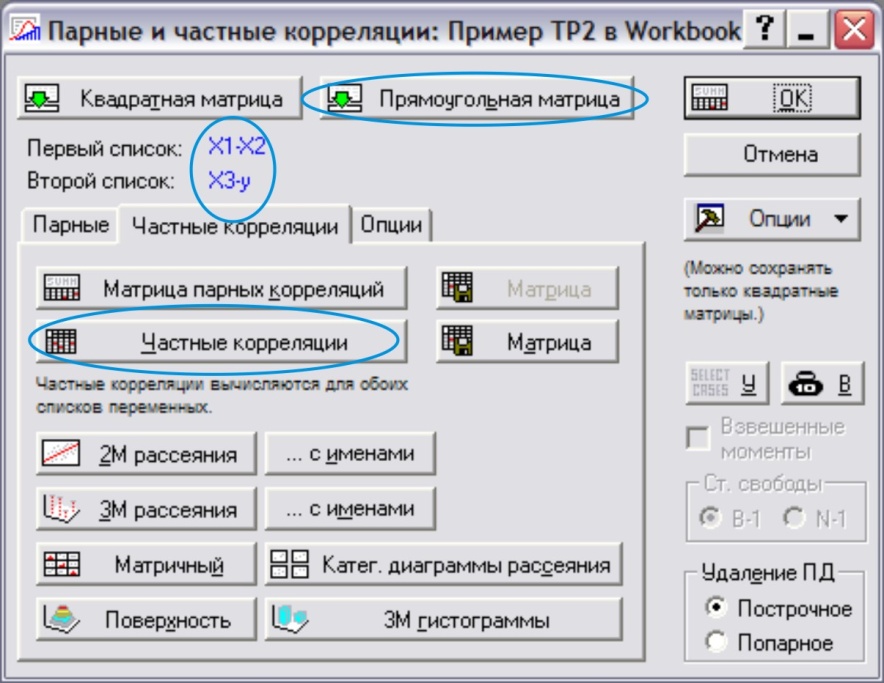
Рис.6
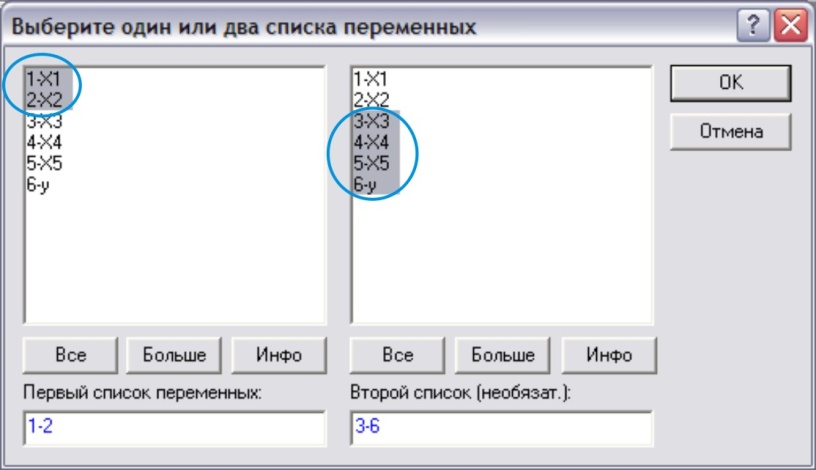
Рис.7
Вернулись в стартовое окно. Выбрать кнопку Частные корреляции
В результате получаем таблицу, в которой указаны частные коэффициенты корреляции между двумя выбранными переменными (X1 и X2).

Аналогично можно рассчитать частные коэффициенты корреляций между всеми переменными. Интересно было бы отследить частные коэффициенты корреляции для предполагаемых мультиколлинеарных факторов:
X2 и X4

X2 и X5

X4 и X5

Оказывается переменные X4 и X5 очень слабо связаны, причем эта связь не подтверждается при проверке гипотезы о значимости частного коэффициента корреляции:
H0: r=0
H1: r≠0 с помощью статистики 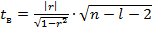 , которая при выполнении нулевой гипотезы имеет распределение Стьюдента с k=(n-l-1) степенями свободы, где l – число фиксируемых факторов.
, которая при выполнении нулевой гипотезы имеет распределение Стьюдента с k=(n-l-1) степенями свободы, где l – число фиксируемых факторов.
Для нашего примера n=52, l=4, тогда k=52-4-2=46; с помощью вероятностного калькулятора вычисляем 
Частные коэффициенты корреляции
| Значение | t-статистика | t кр | Вывод | ||
| rx1x2/… | -0,140 | 0,969338168 | < | 2,012896 | не значим |
| rx2x4/… | 0,580 | 4,881167757 | > | 2,012896 | значим |
| rx2x5/… | 0,700 | 6,71988562 | > | 2,012896 | значим |
| rx4x5/… | -0,090 | 0,619523084 | < | 2,012896 | не значим |
Большое значение парного коэффициента корреляции между переменными X4 и X5 – результат косвенного влияния переменной X2, которая действительно тесно связана и с X4, и с X5.
Вычисление множественных коэффициентов корреляции позволяет оценить тесноту связи каждой переменной со всеми остальными.
При этом в качестве исходной матрицы корреляций рассматривается матрица корреляций объясняющих факторов (у нас X1 – X5) (если, конечно, известно, какая переменная берется в качестве объясняемой).
Если же непонятно, какую переменную брать в качестве объясняемой (невозможно установить из смысла переменных или из экономической теории), то вычисление множественных коэффициентов корреляции позволяет определить эту переменную: в качестве объясняемой переменной выбирается та, для которой коэффициент множественной корреляции R (или коэффициент детерминации R2) будет максимальным.
Существуют формулы, основанные на матричном исчислении, которые позволяют найти R и R2. Мы воспользуемся возможностью пакета Statistica: построим уравнения регрессии каждого фактора на все остальные. Причем, нас будет интересовать только показатель R или R2.
Выполним команду Анализ→Множественная регрессия. (рис.8) В появившемся окне нажать кнопку Переменные. В окне «Списки зависимых и независимых переменных» слева указать,например, переменную X1, а справа – все остальные факторные переменные X2, X3, X4, X5. → ОК
Рис. 8
Вы вернетесь в стартовое окно. Нажатие кнопки ОК приведет к построению уравнения регрессии X1 от всех остальных факторов. Появится окно «Результаты множественной регрессии» (рис. 9)
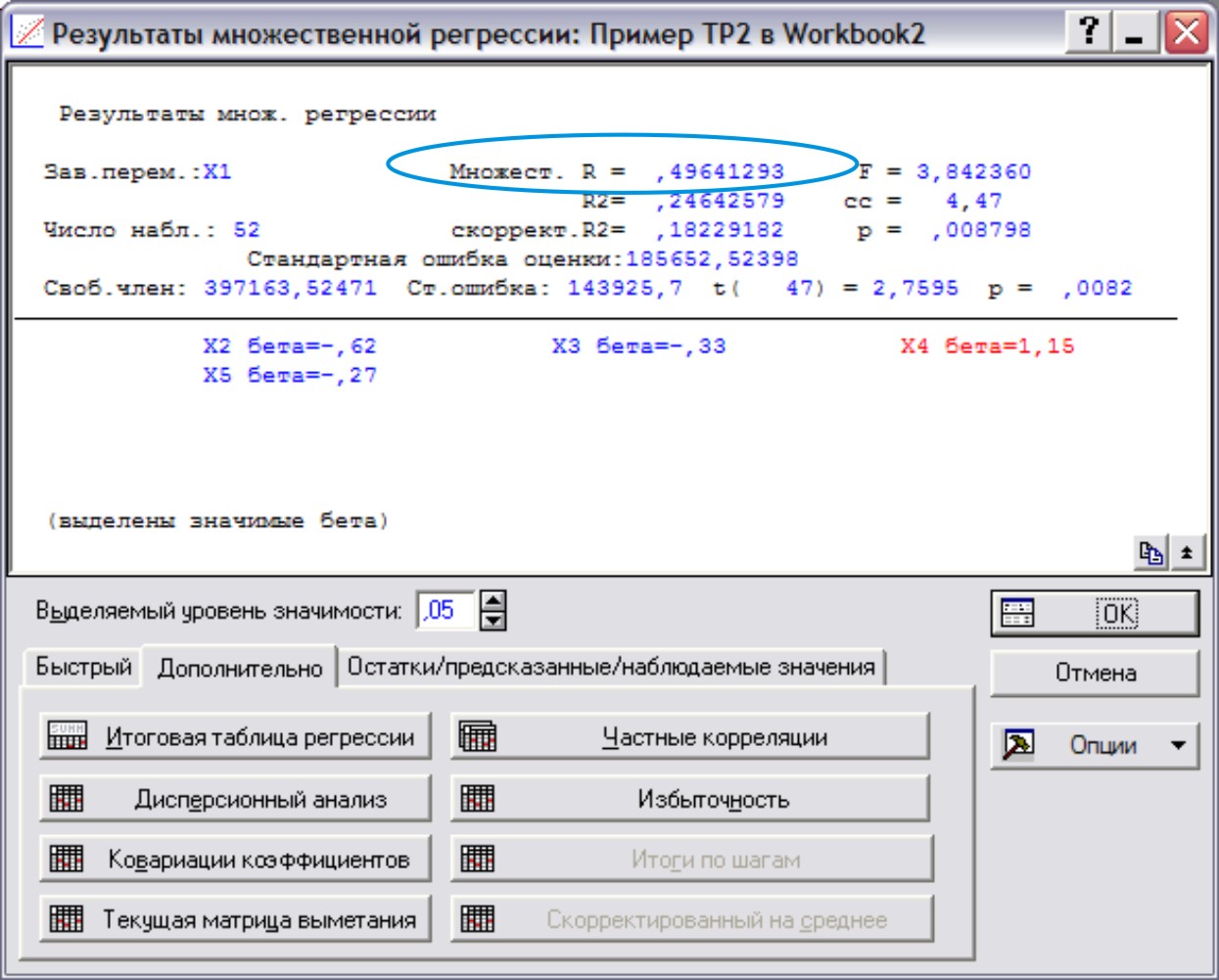
Рис.9
В нем в первой строчке прописан искомый параметр – множественный коэффициент корреляции – 0,496. Выпишем его отдельно на листок. Нажмем кнопку Отмена. Прдолжим процедуру, взяв в качестве объясняемой переменной другой фактор – X2, а в качестве объясняющих – X1, X3, X4, X5. В результате получим следующие коэффициенты множественной корреляции:
| Rx1 | 0,496 |
| Rx2 | 0,981 |
| Rx3 | 0,712 |
| Rx4 | 0,934 |
| Rx5 | 0,974 |
Замечание: Если бы у нас не была указана объясняемая переменная Y, то в результате сравнения множественных коэффициентов корреляции (или коэффициентов детерминации) мы выбрали бы переменную X2 в качестве объясняемой и переименовали бы ее в Y.
Для определения спецификации модели (линейные-налинейные зависимости Y от Xi) воспользуемся возможностью программы Statistica: построим графики зависимости Y от всех факторов: Графика→Матричные графики
В появившемся окне выберем опцию Прямоуг. Матрица рассеяния (рис. 10) и нажмем кнопку Переменные.
Рис.10.
Появится окно выбора переменных, в котором следует указать независимые переменные (все Xi) – в левой части окна, и зависимую – Y – в правой. ОК. (рис. 11)
Рис.11
В стартовом окне нажать кнопку ОК. В результате получим графики, анализируя которые можно выдвинуть гипотезы о виде зависимости результата от каждого из факторов (рис. 12).
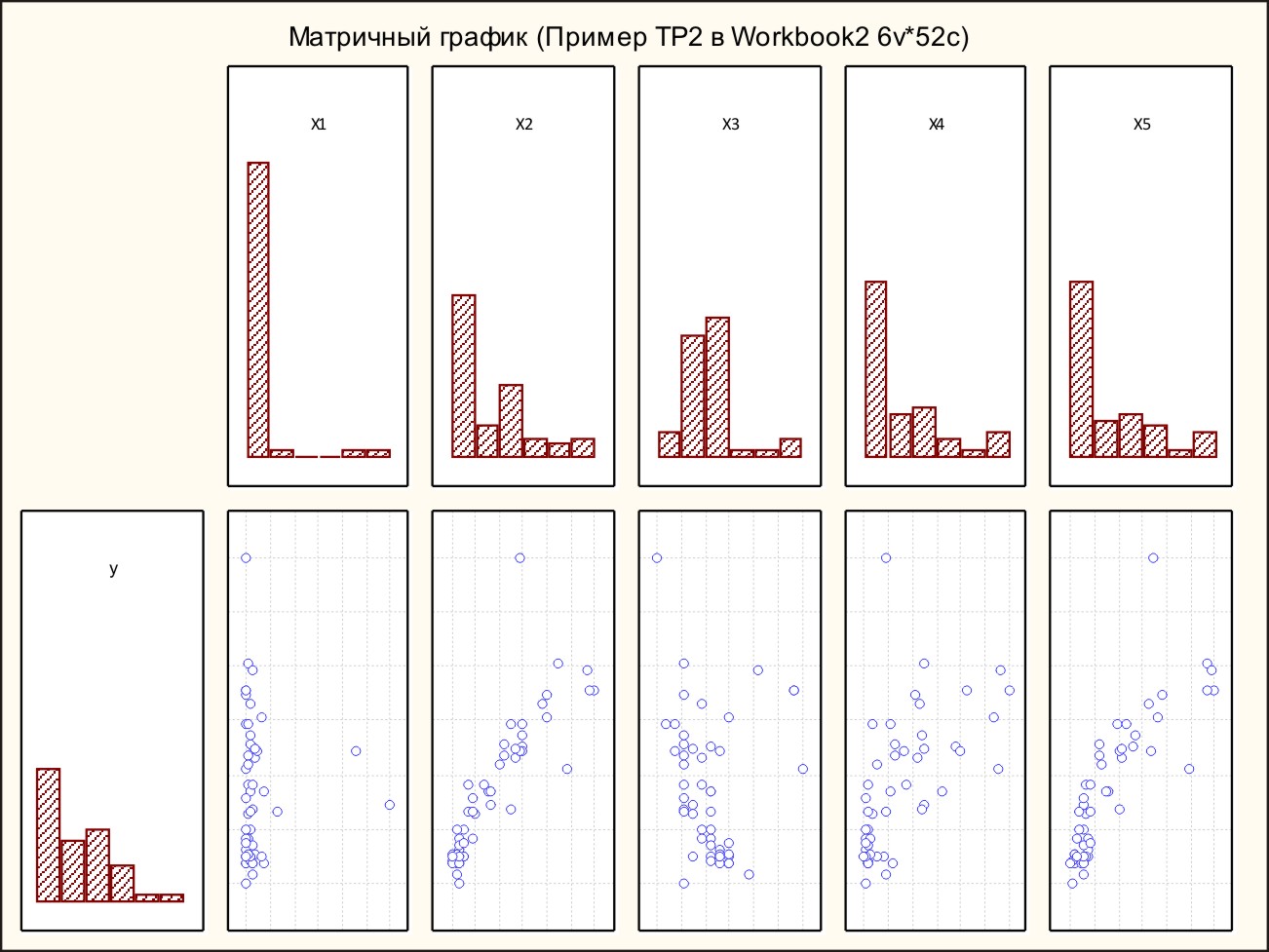
Рис. 12.
Вид графиков рассеяния точек наводит на мысль, что зависимость Y от X2, X4 и X5 – прямая, а от X3 – обратная. Причем, зависимость Y от X2 и X5 напоминает по виду логарифмическую кривую или параболу. Зависимость Y от X4 скорее всего линейная или гиперболическая. Относительно вида зависимости Y от X1 затруднительно что-либо предположить. Нам известно из предыдущих вычислений, что коэффициент корреляции для переменных Y и X1 – незначим, т.е. равен нулю.
Задание 2. Построение линейной формы с полным набором факторов и оценка качества построенной модели;
Строим линейную модель множественной регрессии со всеми переменными:
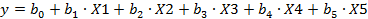
Выполним команду Анализ→Множественная регрессия. (рис.13) В появившемся окне нажать кнопку Переменные. В окне «Списки зависимых и независимых переменных» слева указать зависимую переменную Y, а справа – все остальные факторные переменные X1, X2, X3, X4, X5. → ОК
В стартовом окне, куда мы возвратились, нажать кнопку ОК.
Рис. 13
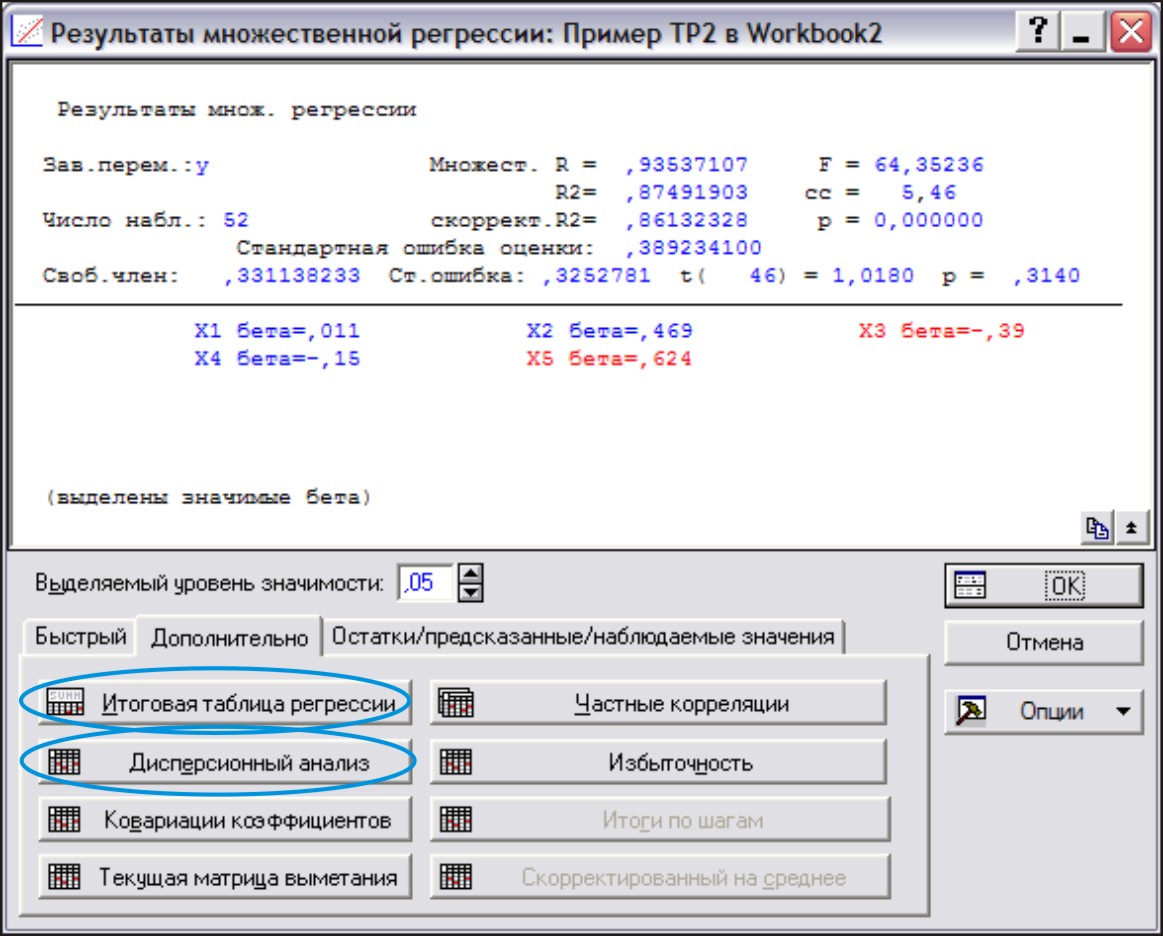
В результате появится окно итогов построения модели множественной регрессии (рис.14)
Рис. 14
Для анализа построенной модели выведем результаты – кнопка Итоговая таблица регрессии.
В результате Statistica выдает две таблицы: Итоговые статистики и Итого регрессии

Таблица. Итоговые статистики
Таблица. Итоги регрессии

Уравнение регрессии имеет вид:
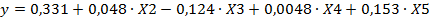

В последней таблице значимые коэффициенты при переменных выделены красным цветом.
1) Проверим значимость уравнения регрессии в целом. Проверяемая гипотеза:
H0: r=0
H1: r≠0 с помощью статистики 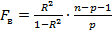 , которая при выполнении нулевой гипотезы имеет распределение Фишера с k1=p и k2=n-p-1 степенями свободы.
, которая при выполнении нулевой гипотезы имеет распределение Фишера с k1=p и k2=n-p-1 степенями свободы.
Для нашего примера n=52, p=5 (число факторов), тогда k1=54; k2=52-5-1=46.
Критическое значение показателя 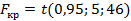 может быть вычислено с помощью вероятностного калькулятора в программе Statistica: Анализ → Вероятностный калькулятор → Распределения
может быть вычислено с помощью вероятностного калькулятора в программе Statistica: Анализ → Вероятностный калькулятор → Распределения
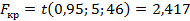 .
.
Выборочное значение F-критерия указано в обеих таблицах: Fв=64,352. Нажав на кнопку Дисперсионный анализ, можем подробно рассмотреть составляющие, с помощью которых вычисляется F-статистика. Гипотеза H0 отклоняется. Уравнение в целом признается значимым.

Коэффициент детерминации R2=0,87. Это означает, что 87% вариации результативного признака Y объясняется данным уравнением регрессии.
Но многие коэффициенты данного уравнения незначимы.
2) Для проверки значимости коэффициентов используется t-статистика Стьюдента, которая вычисляется для каждого коэффициента:
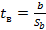 , где b – числовое значение коэффициента, Sb – его среднеквадратическое отклонение (в таблице – Стд. Ош. В); tв для каждого коэффициента представлены в таблице в столбце t(46). Если выполняется гипотеза H0: bi=0, то вычисленное значение t-статистики по модулю должно быть меньше критического значения
, где b – числовое значение коэффициента, Sb – его среднеквадратическое отклонение (в таблице – Стд. Ош. В); tв для каждого коэффициента представлены в таблице в столбце t(46). Если выполняется гипотеза H0: bi=0, то вычисленное значение t-статистики по модулю должно быть меньше критического значения
tкр=t(0,95; n-p-1)=t(0,95; 46). В этом случае коэффициенты признаются незначимыми (равными нулю).
С помощью вероятностного калькулятора находим tкр=2,0128.
Таким образом подтверждается незначимость коэффициентов b0, b1, b2, b4.
Задание 3. Построение линейной формы с информативными факторами и оценку качества построенной модели;
Вызовем модуль Множественная регрессия, определим, как и при выполнении задания 2, зависимую и независимые переменные. Для выполнения пошаговой процедуры включения (исключения) факторов выставим флажок у опции Пошаговая или гребневая регрессия→ ОК (рис. 15)
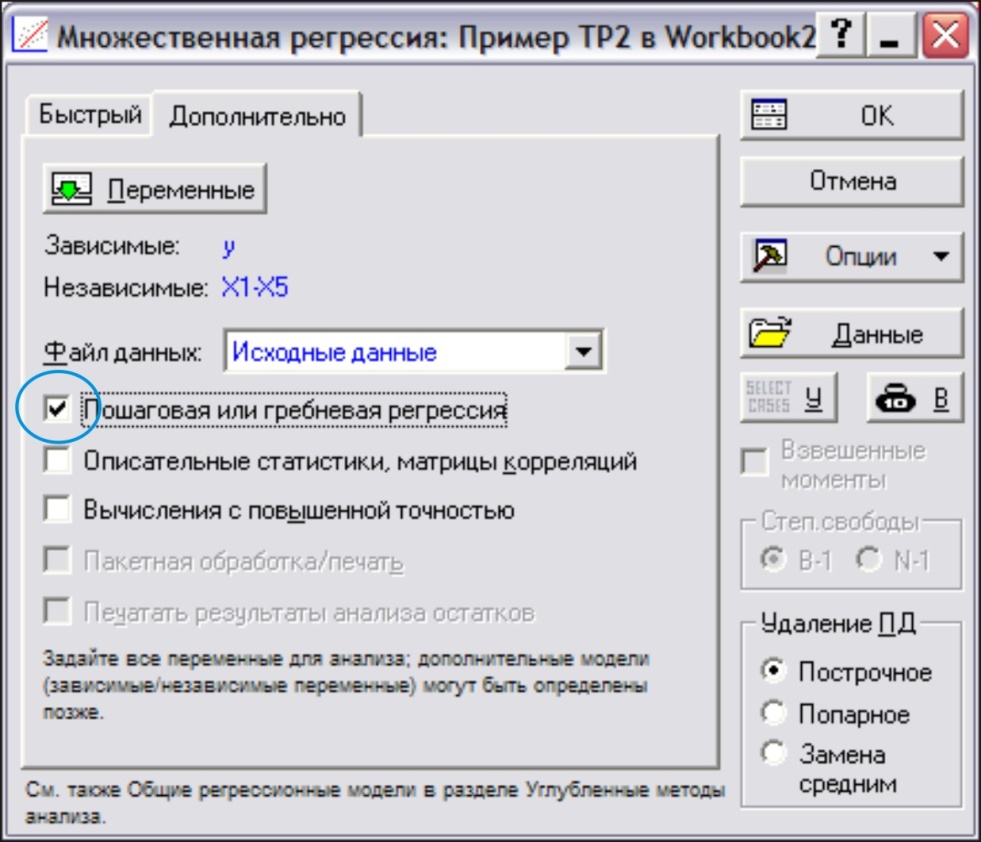
Рис. 15
Появится диалоговое окно, в котором следует установить параметры пошаговой процедуры (рис. 16). → ОК
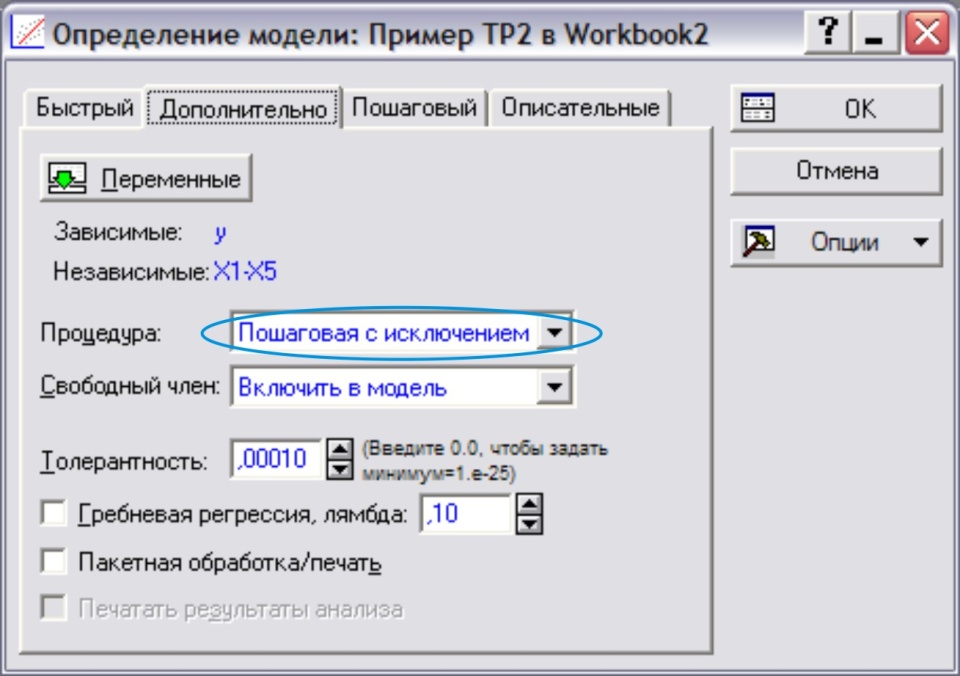
Рис. 16
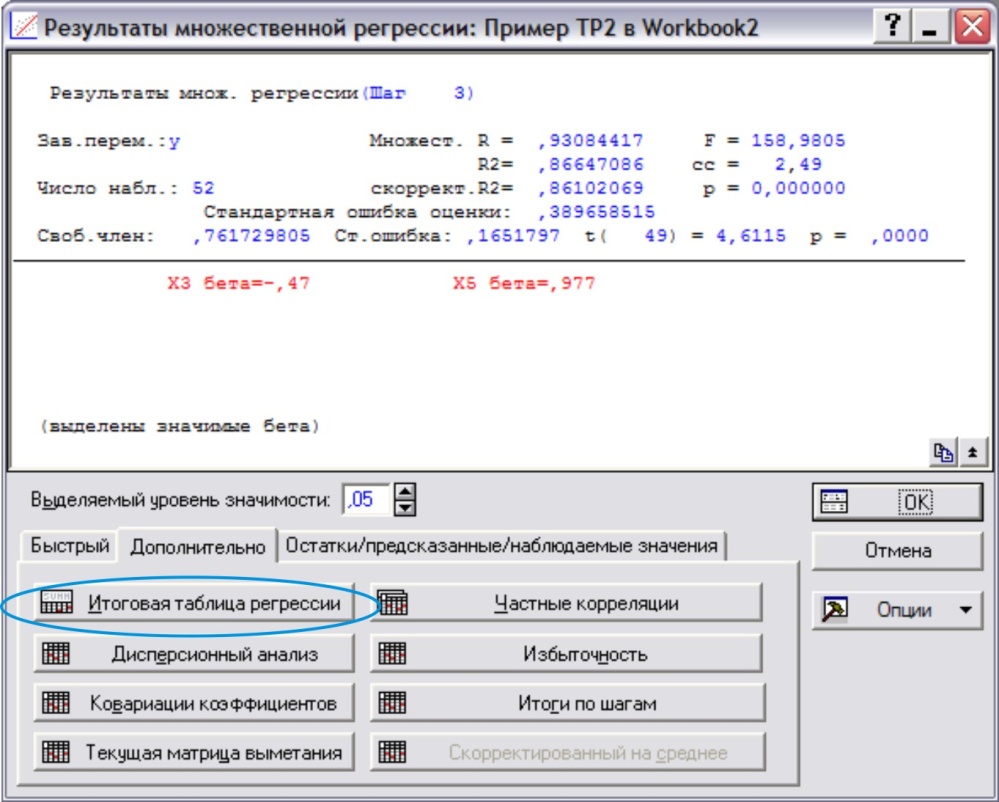
Появится окно с результатами регрессии.(рис.17)
Рис. 17
Нажатие на кнопку Итоговая таблица регрессии выводит также как и при выполнении Задания 2, две таблицы (здесь приводятся из отчета)


Уравнение регрессии имеет вид:
Y=0,762 - 0,148 X3 + 0,6499 X5; R2=0,866; R2корр=0,861; F=158,98
Действуя по той же схеме, что и в Задании 2,
определяем Fкр = F(0,95; 2; 52-2-1)=F(0,95; 2; 49)=3,186582,
определяем tкр=t(0,95; 52 – 2 – 1)=t(0,95; 49)=2,00957.
Сравнивая их с полученными в таблицах, делаем вывод о значимости уравнения в целом и об отличии от нуля всех вычисленных коэффициентов.
Коэффициент детерминации R2=0,866. Это означает, что 86% вариации результативного признака Y объясняется данным уравнением регрессии. Интерпретация коэффициентов:
- увеличение смертности (X3) в среднем на 1 человека (на 1000 чел.) приводит к уменьшению прироста населения приближенно на 0,15% при неименном среднем числе детей в семье (X5);
- увеличение среднего числа детей в семье на 1 ребенка приводит к увеличению прироста населения на 0,65% при неизменном уровне смертности.
Сопоставление по силе влияния факторов на результат можно провести, сравнивая безразмерные БЕТА-коэффициенты (по модулю): сильнее влияет фактор X5, т.к. β5=0,977 больше β3=0,467.
Замечание: Поскольку после построения нелинейной модели регрессии (Задание 4), необходимо будет проверять для каждой из моделей выполнение предпосылок МНК, то лучше этот анализ провести, не выходя из модуля решения данной задачи в пакете Statistica.
Date: 2015-07-23; view: 447; Нарушение авторских прав