
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Краткая теория. Лабораторная задача QM-7
|
|
Лабораторная задача QM-7
Распад связанного состояния частицы.
Краткая теория.
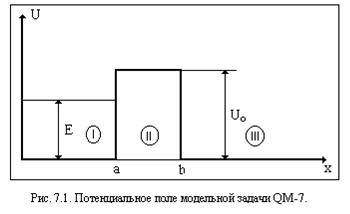
Пусть частица находится в потенциальном поле, представленном на рисун-
ке 7.1. По классическим представлениям если энергия частицы E<U0, как показано на рис. 7.1, то частица движется в области I потенциального поля.
Поведение квантовой частицы рассмотрим на примере решения стационар-
ного уравнения Шредингера для кусочно-непрерывного потенциального
поля
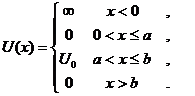 (7.1)
(7.1)
Пусть также выполнены условия:
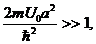
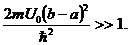
Физический смысл первого из этих условий заключается в том, что в по-
тенциальной яме 0 < x < a существует уровень энергии (более правиль-
но было бы говорить о квазиуровне) с величиной Е < U0. Второе условие
означает, что прозрачность потенциального барьера a < x < b экспонен-
циально мала.
Как обычно это делается при решении уравнения Шредингера для части-цы, находящейся в кусочно-непрерывном потенциальном поле, разобьем об-
ласть 0 < x < ¥ на три области (смотри рис. 7.1). Решение стационарного
уравнения Шредингера в каждой из трех областей имеет вид:
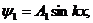
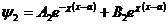 , (7.2)
, (7.2)
 |
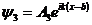 ,
,
где 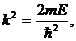
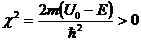 .
.
При записи этих решений было учтено, что в области III существует толь-
ко уходящая от барьера волна, возникающая в результате просачивания час-
тицы через потенциальный барьер. Кроме этого, принято для области I, что
ψ1=0 при x=0, так как в этой точке U → ¥.
Из условия непрерывности волновой функции и ее первых производных на
границах барьера находим:
A1 sin ka = A2 + B2,
A2 cos ka = 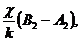
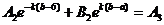 , (7.3)
, (7.3)
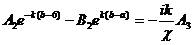 .
.
Условие совместимости этой системы приводит к следующему уравнению:
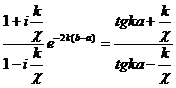 . (7.4)
. (7.4)
При b – a → ¥ прозрачность барьера стремится к нулю, а уравнение (7.4)
сводится к уравнению для определения дискретных энергетических уровней
в потенциальной яме в области I. Это уравнение имеет вид:
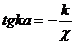 (7.5)
(7.5)
Приближенное решение уравнения (7.4) при выполнении условий ka>>1
и χ(b-a)>>1 может быть записано в виде:
k = k0 - iδ, (7.6)
где δ<< k0, а k0 – решение уравнения (7.5).
Из (7.4) следует, что в первом приближении по 
δ a ~  . (7.7)
. (7.7)
Переходя к энергиям, получим:
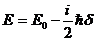 , (7.8)
, (7.8)
где 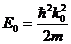 - энергия уровня при нулевой прозрачности барьера.
- энергия уровня при нулевой прозрачности барьера.
Наличие мнимой части в (7.8) означает убывание по экспоненциальному
закону вероятности обнаружить частицу внутри потенциальной ямы
(область I на рис. 7.1). Действительно, для величины |ψ(x,t)|2 имеем
|ψ(x,t)|2~ 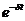 . (7.9)
. (7.9)
Полученные выражения позволяют связать между собой постоянную рас-
пада δ и прозрачность барьера D:
 |
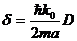 , (7.10)
, (7.10)
где 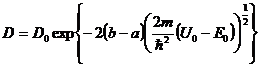 . (7.11)
. (7.11)
Учитывая, что 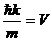 , где V – скорость частицы, выражение (7.10) мож-
, где V – скорость частицы, выражение (7.10) мож-
но записать в виде 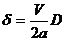 . (7.12)
. (7.12)
Здесь 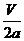 - частота соударений частицы со стенками, расстояние между которыми равно а. Поэтому выражение (7.12) может быть понято следу-
- частота соударений частицы со стенками, расстояние между которыми равно а. Поэтому выражение (7.12) может быть понято следу-
ющим образом. Частица сталкивается с частично прозрачной стенкой с
частотой 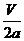 . При этом с вероятностью D она туннелирует через барьер.
. При этом с вероятностью D она туннелирует через барьер.
Поэтому среднее время жизни частицы в яме равно 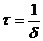 . Вероятность
. Вероятность
обнаружения частицы внутри потенциальной ямы уже не будет постоянной,
а будет зависеть от времени. Такие состояния называются квазистационар-ными. Легко видеть, что при возрастании ширины барьера b-a вероятность
туннельного эффекта экспоненциально падает, вследствие чего время жизни
τ растет. Существенно, что энергия частицы внутри потенциальной ямы уже
не имеет строго определенного значения: энергетические уровни оказывают-ся размытыми. Ширину уровней можно определить с помощью соотношения
неопределенностей:
ΔЕ·τ ~ ћ (7.13)
С увеличением проницаемости барьера τ убывает, что приводит к возраста-нию ширины ΔЕ. И наоборот, для абсолютно непрозрачного барьера τ→¥ а ΔE→0, что соответствует стационарному состоянию с точно определен-
ным значением энегии.
Изложенная теория хорошо объясняет α- распад атомных ядер. В резудьта-те α- распада атомное ядро испускает α- частицу (т. е. ядро атома гелия). Ква-
нтовая механика объясняет α- распад как туннелирование α- частиц через по-
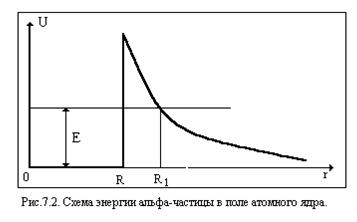
тенциальный барьер непрямоугольной формы. На рис. 7.2 изображена схема
потенциальной энергии α- частицы в поле радиоактивного ядра. Здесь при
r<R (внутри ядра) потенциальная энергия α- частицы равна нулю. При
r>R на α- частицу действуют силы кулоновского отталкивания с потенциа-льной энергией
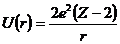 ,
,
где Ze – заряд радиоактивного ядра, 2e – заряд α- частицы. Прозрачность
потенциального барьера непрямоугольной формы вычисляется интегриро-
ванием:
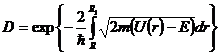 (7.14)
(7.14)
Здесь m – масса α- частицы, E – ее энергия. Среднее время жизни радиоак-
тивного ядра вычисляется по формуле 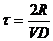 , где V – скорость α- части-цы в ядре. Расчет по этим формулам даст следующее выражение для τ,
, где V – скорость α- части-цы в ядре. Расчет по этим формулам даст следующее выражение для τ,
полностью совпадающее с опытным законом Гейгера-Неттола:
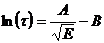 , (7.15)
, (7.15)
где А и В – постоянные.
Date: 2015-07-22; view: 343; Нарушение авторских прав