Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Дәріс 2 Цифрлық құрылғыларды логикалық жобалау негіздері. Бульдік алгебра. Бір және екі айнымалы бульдік функциялар
|
|
Буль алгебрасының негізгі түсініктері. Екілік сандармен әр түрлі адамдар орындай алатын құрылғыларды екілік сандардың функционалдық түрлендіргіші ретінде қарауға болады. Мұндай түрлендіргіштерде бастапқы санның жеке разрядтары аргумент, ал алынған нәтижелердің разряды функция болып табылады. Арифметикалық амал орындалатын құрылғының әр кірісіне бастапқы санның бір разряды беріледі (0 немесе 1), ал оның әр шығысынан нәтиженің екілік разряды (0 немесе 1) алынады.
Осындай құрылғыларды талдау және синтездеу үшін екілік айнымалыларымен әр түрлі операция жасауға мүмкіндік беретін математикалық аппарат қажет. Мұндай аппараттың негізін өткен ғасырдың ортасында ағылшын математигі Д.Буль тұжырымдаған болатын. айнымалы шамалар мен олардың функциялары тек екі мән (0 немесе 1) қабылдайтын болса, онда бульдік немесе логикалық айнымалылар мен функция деп аталады. Логикалық функицялардың қасиеттері математикалық логикада зерттеледі.
Екілік айнымалылар жиынтығымен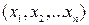 
анықталатын және өздері не ноль, не бір деген мәндер қабылдайтын функцияларды логика алгебрасының функциялары (ЛАФ) деп атайды, ЛАФ берілуі деп оның 0 немесе 1 деген мәні әрбір мүмкін болған аргументтер жиынтығының мөлшері n разряд арқылы кескінделетін әр түрлі сандарға тең, яғни 2 n. Барлық мүмкін болатын аргументтер жиынтығы мен оларға сәйкес функциялар мәндерін бір кестеге жинақтасақ ЛАФ кестелік берілуін немесе оның шындық кестесін аламыз: 
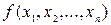. Егер екі ЛАФ 
және 
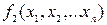әр түрлі аргументтер жиынтығында бірдей мәнге ие болса, онда 
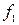және 
функцияларын өзара тең деп атаймыз: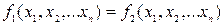 
.
Функция аргументтерінің ішінде оның мәндеріне әсерін тигізбейтін жалған аргументтер болуы мүмкін. Егер функиялар арасында мынадай арақатынас болса: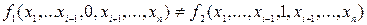 
, онда 
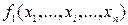функциясы xi аргументінен айтарлықтай тәуелді болады. Өйткені әрбір аргументтер жиынтығында ЛАФ екі мәннің бірін қабылдай алады десек, онда n аргументпен анықталатын ЛАФ мөлшері шекті, ол 
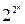-не тең. Бұл тұжырымның дәлелі әрбір ЛАФ екілік жиынтық түрінде 
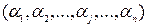қарауға болатынынан шығады, бұл жерде 
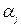аргументтерінің j жиынтығында алатын ЛАФ мәні. Ал мұндай жинақтар саны 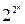формуласымен анықталады. Әр түрлі ЛАФ саны өскен сайын өте тез еселенеді. Мысалы: n = 4 болғанда ЛАФ саны 5536. Бірақ осы 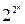функциялардың ішінде n аргументіне айтарлықтай тәуелді функциялармен қатар кейбір аргументтер бөлігінен тәуелсіз функциялар да кездеседі. n аргументтерден айтарлықтай тәуелді ЛАФ санын мынадай рекуренттік қатынаспен анықтауға болады: 
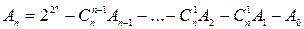, бұл жерде 
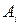- n аргументпен анықталатын ЛАФ саны, 
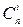- элементтен i -ден алынған терулер саны.
Мысалы үшін аргумент үшін А 3-ті анықтуа керек. алдын ала А 0, А 1 және А 2 мәндерін анықтаймыз. А 0 мен А 1-ді бір аргументтің (х -тің) кестелік берілу мәнінен анықтауға болады.
| x | f 1 | f 2 | f 3 | f 4 |
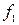мен функцияларында х жалған аргумент болады, сондықтан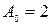 
. Аргумент мәні өзгертуімен өз мәнін өзгертетін функцияларға 
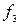және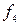 
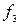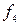жатады, басқаша айтқанда және функциялары х аргументіне айтарлықтай тәуелді (
). 
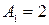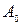және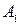 
мәндерін біле отырып, А мәнін есептеп шығаруға болады: 
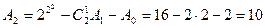бұдан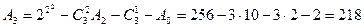 
. Сонымен үш айнымалымен анықталатын 256 ЛАФ санының тек 218 ЛАФ-ы ғана үш аргументке айтарлықтай тәуелді болады.
Матрицалық функция кезінде бульдік функциялар кестемен беріледі. Бульдік функцияға мысал 2.2-кестеде берілген. 2.3-кестеде осы функцияның кестелік берілуі көрсетілген, бірақ екілік жиынның орнына олардың ондық баламалары келтірілген.
2.2 – кесте.
| Х1, х2, х3 | f |
| 0 0 0 0 0 1 0 1 0 0 1 1 1 0 0 1 0 1 1 1 0 1 1 1 |
2.3 – кесте.
| Жиын нөмірі | f |
Графиктік тәсілде бульдік функция n -өлшемді куб көмегімен беріледі. Геометриялық мағынада әрбір екілік жиын n- өлшемді вектор, n- өлшемді нүктені анықтайды. Төмендегі суретте 3-өлшемді кубтың геометриялық көрсетілуі берілген
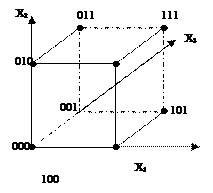
2.2 – сурет. Кестеде берілген бульдік функцияның геометриялық көрсетілімі
Бір және екі айнымалы бульдік функциялар. Кеңірек қолданылатын бір немесе екі айнымалыдан құралған бульдік функцияларды қарастыралық. Бір айнымалылы функция 2.4-кестеде берілген.
2.4 – кесте
| х | f0 f1 f2 f3 |
| 0 0 1 1 0 1 0 1 |
f0(x)=0-0 тұрақтысы
f1(x)=х - функциясы
f2(x)= 
терістеу (инверсия)
f3(x)=1 - тұрақтысы
Логика алгебрасының қарапайым функциялары. ЛАФ кестелік берілу тәсілі өте қарапайым болғанымен, ол ыңғайсыз және ықшам емес болып келеді. Мысалы n=8 ЛАФ берілсі 28=256 қатардан (жолдан) тұрады. Сондықтан күрделі логикалық функцияларды қарапайым функциялар арқылы көрсету (кескіндеу) ыңғайлы.
ЛАФ ішінен 14 қарапайым деп аталатын функицяларды оқшау көрсетуге болады. Олар логика алгебрасының теориясын жасауда және оны қолдануда айырықша орын алады. Функциялардың төртеуі 2.5-кестеде берілген: 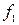-ноль константасы (
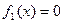), - бірлік константасы (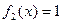
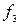), - тепе-теңдік функциясы (
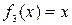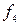), -инверсия функциясы немесе логикалық терістеу ("ЕМЕС") функциясы (
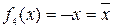). Қалған элементар функцияларды 2.5-кестеде көрсетілгендей екі айнымалымен анықталады. Бұл кестеде жоғарыда анықталған константа 0, константа 1 тепе-теңдік және логикалық терістеу функциялары да келтірілген.
2.5 – кесте
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
|
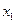
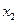
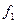
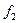
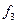
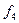
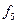
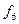
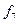
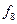
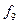
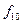
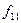
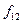
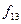
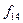
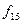
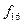
Кестедегі бірінші алты ЛАФ белгілі функциялар: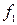 
-"0" константасы, -"1" константасы;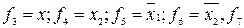 
функциясы дизъюнкция деп аталады. Ол 
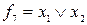түрінде белгіленеді. Дизъюнкиция 1 деген мәнді аргументтерінің кеміне біреуі 1-ге тең болғанда алады; ол 
(
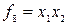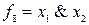) түрінде белгіленеді. Конъюнкция 1 деген мәнді аргументтердің барлығы бірдей 1-ге тең болғанда ғана алады. 
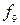функциясы эквиваленттік (пара-парлық) деп аталады, ол 
(
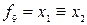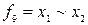) түрінде белгіленеді. Функция 1 деген мәнге аргументтері тең болғанда ие болады. 
функциясы әр аттылық (екі модулімен қосу) деп аталады. Ол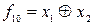 
түрінде белгіленеді. Функция 1 мәнін аргументтер жиынтығының мәндеріне бір-біріне сай келмегенде қабылдайды.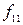 
функциясы 
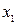дің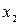 
-ге импликациясы деп аталады. 
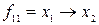түрінде белгіленеді. Функция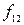 
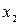-нің 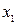-дегі импликацясы деп аталады. 
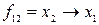түрінде белгіленеді. Функция 
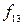Вебба функциясы (Пирс стрелкасы) деп аталады. 
(
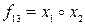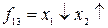) түрінде белгіленеді. Функция 
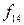- Шеффер функциясы, ол 
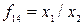түрінде белгіленеді. 
және 
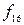функцияларының арнаулы атаулары жоқ. 
, 
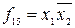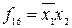. Кейде 
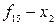-ге тыйым функциялары деп атайды. , 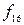функциялары элементар функцияларға жатпайды.
Енді элементар функциялардың қасиеттерін қарайық:
Дизьюнкция мен коньюнкциялар үшін:
1) ауыстырымдылық заңы (коммутативтік қасиет):
; 
;
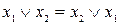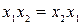2) терімділік заңы:
; 
;
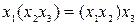3) үйлестіру заңы (дистрибутивтік қасиет): дизьюнкцияға қатысты коньюнкция үшін: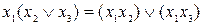 
қатысты орынды. Үлестіру заңы логикалық өрнектердегі жақшаларды ашу ережелерін анықтайды.
Х аргументіне мүмкін болатын әр түрлі мәндер беріп, мына өрнектердің орынды екеніне көз жеткізуге болады:
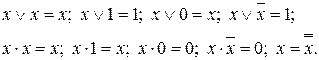
аргументтердің әр түрлі жиынтықтары үшін өрнектердің сол жақтарын және оң жақтарын салыстыра отырып, де Морган заңы деген атпен белгілі қатыстардың орынды екенін байқауға болады:
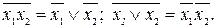
Де Морган заңдары және оның салдары кез келген айнымалылар санына тура келеді:
Екі модулімен қосу функциясын былай көрсетуге болады:
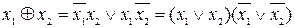
Бұл функция үшін мына заңдар орындалады:
1) ауыстырымдылық заңы: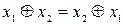 
;
2) терімділік заңы: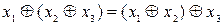 
;
3) үлестіру заңы: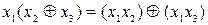 
.
Қаралып отырған функция үшін және мынадай арақатынастар орын-алады:
Импликация функциясын төмендегідей көрсетуге болады:
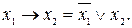
Бұл функция үшін мынадай арақатынастар тура болады:
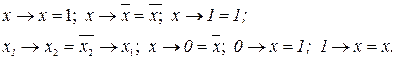
Шеффер функциясы коньюнкция функциясының терістеуі болып табылады:
.
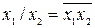Импликация функциясын төмендегідей көрсетуге болады:
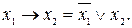
Бұл функция үшін мынадай арақатынастар тура болады:
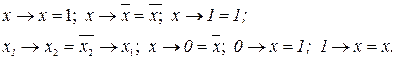
Шеффер функциясы коньюнкция функциясының терістеуі болып табылады: 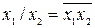. Бұл функция мына арақатынастарға ие болады: 
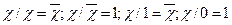. Ауыстырымдылық заңы Шеффер функциясында тек екі айнымалылар үшін орындалады: 
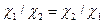Шеффер функциясын пайдалана отырып логикалық өрнектерді түрлендіруге мүмкіндік беретін кейбір формулалар алуға болады:
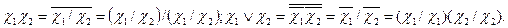Пирс (Вебба) функциясы дизьюнкция функциясының терістелуі болып табылады: 
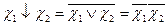. Бұл қарапайым функцияға төмендегі арақатынастар тура келеді: 
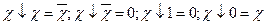. Пирс (Вебба) функциясы тек ауыстырымдылық заңына бағынады: 
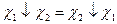Дизьюнкция, коньюнкция, логикалық терістеу, Пирс (Вебба) функцияларының арасында өзара мынадай байланыстарды байқауға болады: 
.
Қаралған қарапайым функциялар жаңа ЛАФ алуға мүмкіндік береді. Ол екі жолмен: аргументтерді қайта номерлеу және функциялардағы аргументтер орнына жаңа функциялар қою арқылы алынады. Осы екі операцияны бастапқы функцияларға (f1,f2,…,fk) қайта қайта қолдану жолымен алынған функция f1,f2,…,fk функцияларының суперпозициясы деп атайды.
Date: 2015-06-11; view: 4076; Нарушение авторских прав