Глава 8. Образы хаоса

Математик Майкл Барнсли встретил Митчелла Файгенбаума во время конференции на Корсике в1979-м году. Барнсли, недавний выпускник Оксфорда, только-только познакомился с понятием всеобщности, удвоением периодов и бесконечным каскадом бифуркаций. «Отличная идея, – подумал он. – И конечно, все набросятся на нее, чтобы отхватить себе по кусочку». Барнсли тоже присмотрел себе кусочек, не замеченный еще ни одним из конкурентов. Откуда происходили эти циклы (2,4,8,16), эти последовательности Файгенбаума? Появились ли они, будто по мановению волшебной палочки, из математической пустоты или содержали намек на нечто более глубокое? Барнсли интуитивно чувствовал, что они – часть какого-то невероятного фрактального объекта, ускользавшего до сих пор из поля зрения ученых.

Джон Хаббард начал экспериментировать, рассматривая метод Ньютона не как средство решения задач, а как саму задачу. Он взял в качестве примера простое кубическое уравнение х³ – 1 = 0, при решении которого требуется найти кубический корень из единицы. В случае с действительными числами решение вполне тривиально – единица. Однако данный многочлен имеет также два комплексных корня: –1/2 + i и –1/2 – i . Нанесенные на комплексную плоскость, три указанных корня образуют равносторонний треугольник, одна вершина которого будет находиться на трех часах, другая – на семи часах, и третья – на одиннадцати часах. Коль скоро в качестве начальной точки выбрано любое комплексное число, вопрос заключается в том, чтобы увидеть, какое именно из трех решений даст вычисление по методу Ньютона. Это все равно, что рассматривать данный метод как динамическую систему, а три решения – как три аттрактора. Или представить комплексную плоскость в виде поверхности, спускающейся к трем углублениям. Мраморный шарик, начав катиться с любой точки на плоскости, приведет в одну из долин. Какую?

Компьютер Хаббарда переходил от точки к точке, рассматривая Ньютоновым методом каждую из них и кодируя результат определенным цветом. Те начальные точки, которые вели к первому решению, стали синими, точки, генерировавшие второе решение, – красными, а тем, которые давали третий результат, был присвоен зеленый цвет. Граница между двумя цветами никогда полностью не формировалась, и даже при увеличении линия между зеленым пятном и синей областью включала в себя клочки красного цвета.

Множество Мандельброта, как любят повторять его почитатели, является наиболее сложным объектом во всей математике. Если разглядывать модель в цвете на подходящем экране, множество Мандельброта кажется более фрактальным, нежели сами фракталы, настолько оно изобилует сложностью, пронизывающей все масштабы картины. Неисчислимое многообразие фрактальных форм может быть образовано итерацией в комплексной плоскости, но система Мандельброта была одной-единственной (рис. 10).

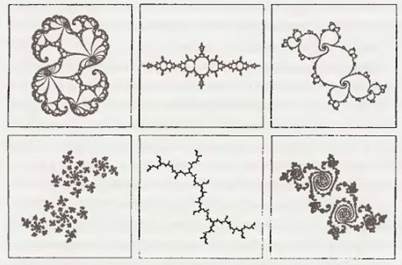
Рис. 10. Примеры изображений, полученных с помощью множеств Джулиа

В отличие от традиционных геометрических форм, таких как окружности, эллипсы и параболы, система Мандельброта не допускает никаких сокращенных вариантов. Определить, какая форма подходит к каждому конкретному уравнению, удается только методом проб и ошибок.

Такое объединение вселенной форм с миром чисел говорило о разрыве с прошлым. Новые геометрии всегда начинаются с того, что кто-нибудь пересматривает базовый постулат. Предположим, говорит ученый, что пространство определенным образом искривлено, – и в результате получается странная пародия на Евклида, геометрия Римана-Лобачевского, которая стала основой общей теории относительности. Дальше – больше… Допустим, что пространство может иметь четыре измерения, пять и даже шесть… Вообразим, что число, выражающее измерение, может представлять собой дробь… Представим, что геометрические объекты можно закручивать, растягивать, завязывать узлами… Пусть их можно определить не решением определенного уравнения, а итерацией его с помощью петли обратной связи. Джулиа, Фато, Хаббард, Барнсли, Мандельброт – все эти математики изменили правила создания геометрических форм.

Картезианский и Евклидов методы превращения уравнений в кривые знакомы любому, кто изучал геометрию в средней школе или находил точку по карте по двум координатам. В стандартной геометрии кроме уравнений необходим также и набор чисел, которые уму удовлетворяют, тогда решения уравнения вроде х²+у² = 1 образуют форму, в данном случае – окружность. Другим простым уравнениям соответствуют иные фигуры: эллипсы, параболы, гиперболы конических сечений и даже более сложные формы, порождаемые дифференциальными уравнениями в фазовом пространстве. Но когда геометр прибегает к итерации, вместо того, чтобы решать уравнение, последнее преобразуется из описания в процесс, из статического объекта в динамический. Подставив исходное число в уравнение, мы получим новое число, которое, в свою очередь, даст еще один результат, и так далее. Соответствующие им точки перепрыгивают с места на место. Точка наносится на график не тогда, когда она удовлетворяет уравнению, а тогда, когда она генерирует определенный тип поведения. При этом один из них может представлять собой устойчивое состояние, а другой – неуправляемое стремление к бесконечности.

Майкл Барнсли предложил «игру хаоса». Чтобы сыграть в такую игру, необходим компьютер с графическим пакетом программ и генератором случайных чисел, но в принципе будет достаточно листа бумаги и монетки. Выбираем на листе начальную точку – неважно, где именно. Придумаем два правила – для орла и для решки. Правила указывают, каким образом откладывать новые точки, например: «Переместиться на два дюйма на северо-восток» или «Приблизиться на 25% к центру». Подбрасывая монетку, начинаем отмечать точки. Используем правило орла, когда выпадает орел, и правило решки, когда выпадает решка. Если мы отбросим первые пятьдесят точек, как сдающий карты прячет первые несколько карт при новой сдаче, то обнаружится, что «игра хаоса» воспроизводит не случайное поле или разбросанные точки, а форму, проявляющуюся все более и более четко по мере продолжения игры. Основное предположение Барнсли звучало так: множества Джулиа и другие фрактальные формы, хотя и считаются по справедливости итогом детерминированного процесса, обладают второй равнозначной ипостасью как предел неупорядоченного процесса.

Говоря на языке динамики, формы Барнсли оказались аттракторами. Барнсли быстро обнаружил, что может воспроизвести ставшие уже классическими фракталы из книги Мандельброта. Техника последнего представляла собой бесконечную последовательность построений и совершенствований: скажем, для создания снежинки Коха или ковра Серпински нужно, удалив линейные сегменты, заменить их точно определенными фигурами. Применяя вместо этого «игру хаоса», Барнсли создавал изображения, казавшиеся вначале лишь расплывчатыми карикатурами, но со временем вырисовывавшиеся все более четко. Вместо процесса усовершенствования, в котором не возникало необходимости, использовался лишь один набор правил, с помощью которого в итоге и воплощалась нужная форма.