Глава 3. Взлеты и падения жизни

Биологи XX-го века, обратившись к математике, создали новую дисциплину – экологию, которая, абстрагируясь от реальной жизни сообществ животных и растений, стала рассматривать их как динамические системы. Биология популяций выяснила кое-что об истории возникновения жизни, об отношении хищников и их жертв, о том, как влияет изменение плотности населения в регионе на распространение болезни. Если математическая модель показывала, как процесс развивается, достигает равновесия или затухает, экологи могли представить себе обстоятельства, при которых вероятны подобные события.

В мальтузианской схеме неограниченного увеличения численности популяции значение линейной функции роста всегда будет увеличиваться. Схема же, более приближенная к жизни, должна включать в себя особый фактор, сдерживающий рост, если популяция уже и так велика.

Говорят, что идеи Лоренца по-настоящему открыл Джеймс Йорк и он же дал науке о хаосе ее нынешнее имя. Вторая часть этого утверждения справедлива. Ознакомившись со статьей Лоренца, которая ждала своего часа, Йорк увидел, что подобное поймут и физики. Он направил копию Смэйлу, проставив на видном месте свой адрес, чтобы получить статью обратно.

Смэйл изумился, обнаружив, что безвестный метеоролог десятью годами раньше обнаружил ту неупорядоченность, которую он сам посчитал однажды математически невероятной. И, сняв множество копий со статьи, Смэйл положил тем самым начало легенде об открытии Йорком работы Лоренца – ведь на каждой копии, появившейся в Беркли и других местах, стоял адрес Йорка. Йорк же чувствовал, что физиков учили не видеть хаос. Между тем в повседневной жизни замеченная Лоренцем «сильная зависимость от начальных условий» таится всюду. Йорк понял, беспорядок существует. Физики и математики стремятся обнаружить некую упорядоченность. «Какой прок в хаосе?» – говорят они. Однако ученые должны знать хаос, потому что неизбежно столкнутся с ним.

Почему инвесторы настаивают на существовании цикличности в колебаниях цен на драгоценные металлы? Да потому, что периодичность – наиболее сложное упорядоченное поведение, которое они могут себе представить. Глядя на биржевые сводки, они ищут в скачках курса некий порядок.

Йорк решил донести до физиков то, чего они не разглядели в работах Лоренца и Смэйла. Он написал статью для самого популярного научного издания их тех, где ее могли бы опубликовать, – для «Американского математического ежемесячника». Работа Йорка сыграла свою роль, однако, в конечном счете, самой замечательной ее частью стал интригующий заголовок: «Период с тремя волнами заключает в себе хаос».

Йорк продемонстрировал физикам, что хаос вездесущ, стабилен и структурирован. Он дал повод поверить в то, что сложные системы, традиционно сводившиеся к трудным для решения дифференциальным уравнениям, могли быть описаны с помощью довольно простых графиков.

Советские математики и физики уже давно и упорно пытались постичь природу хаоса, начало этому положили еще работы А.Н. Колмогорова 50-х годов. Более того, советские специалисты, как правило, действовали вместе, что помогало представителям двух дисциплин преодолеть разногласия, столь частые в научной среде других стран.

Чем дольше Мэй рассматривал биологические системы сквозь призму простых хаотических моделей, тем больше он видел моментов, противоречащих общепринятым представлениям (рис. 5). Например, эпидемиологи хорошо знают, что массовые вспышки заболеваний появляются, как правило, с определенной цикличностью – регулярно или иррегулярно. Корь, полиомиелит, краснуха идут в наступление и отступают периодически. Мэй осознал, что колебания могли воспроизводиться нелинейной моделью, и заинтересовался тем, что случится, если система получит внезапный толчок – помеху, вроде массовой вакцинации. Казалось бы, процесс должен плавно изменяться в желаемом направлении. На самом деле, как обнаружил Мэй, начнутся весьма ощутимые колебания.

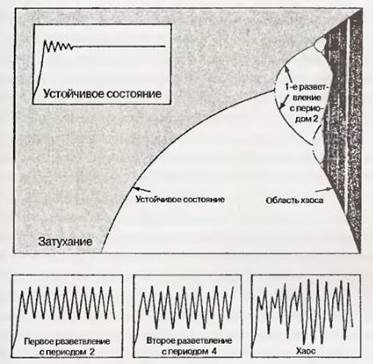
Рис. 5. Удвоение периодов и хаос. Разветвленная диаграмма Роберта Мэя, построенная на основе уравнения х_c = rx(1 – x), где х_c – размер популяции, r – параметр. Показано, каким образом изменение параметра (r) — способности живущей в естественных условиях популяции к снижению и увеличению числа составляющих ее особей – повлияет на поведение системы в целом (х_c). Значения параметра откладываются слева направо по горизонтальной оси; значения численности популяции — по вертикальной. Рост параметра знаменует перегрузку системы, увеличение в ней нелинейного элемента. Когда это значение невелико (слева), популяция угасает. По мере его роста (в центре) популяция достигает равновесия. При дальнейшем увеличении параметра, равновесное состояние расщепляется на две ветви. Начинаются колебания численности популяции между двумя различными уровнями. Расщепления, или разветвления, происходят все быстрее и быстрее. Далее система становится хаотичной (справа), и численность особей может приобретать бесконечное множество значений.