
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Глава 4. Теорема Хана – Банаха для вогнутых функционалов
|
|
Основная теорема 4.1. Пустъ  векторное пространство над
векторное пространство над 
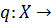
 .
.
(1) Если 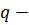 супераддитивный положительно однородный функционал, то для любого
супераддитивный положительно однородный функционал, то для любого 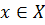 найдется
найдется 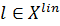 , для которого
, для которого 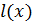
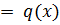 и
и 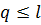 на
на  ; в частности,
; в частности, 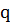 допускает двойственное линейное представление на
допускает двойственное линейное представление на  . (Известная классическая версия Теоремы Хана – Банаха в несколько иной форме).
. (Известная классическая версия Теоремы Хана – Банаха в несколько иной форме).
(2) Если 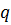 – вогнутый функционал, то для любого
– вогнутый функционал, то для любого 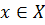 найдется функционал
найдется функционал 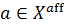 , для которого
, для которого 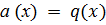 u
u 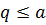 на
на 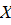 ; в частности,
; в частности, 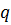 допускает двойственное аффинное представление на
допускает двойственное аффинное представление на  . (Основной полученный результат, более общий и требующий не линейных классов функционалов, а аффинных).
. (Основной полученный результат, более общий и требующий не линейных классов функционалов, а аффинных).
Доказательство. Для доказательства будет использована обобщенная
Теорема Хана-Банаха (о продолжении линейного функционала). Пусть 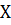 - векторное пространство
- векторное пространство  над
над  ,
, 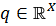 - вогнутый функционал,
- вогнутый функционал, 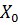 - векторное подпространство в
- векторное подпространство в  . Допустим, что сужение
. Допустим, что сужение 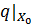 функционала
функционала 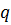 на
на 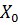 минорирует функционал
минорирует функционал  на
на 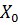 . Тогда существует функционал
. Тогда существует функционал 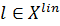 с сужением
с сужением 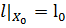 , мажорирующий
, мажорирующий 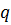 на
на  .
.
Пусть 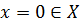 ,
, 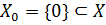 . Тогда нулевой линейный функционал
. Тогда нулевой линейный функционал 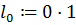 на
на 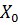 совпадает с сужением вогнутого функционала
совпадает с сужением вогнутого функционала 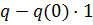 на
на 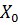 и, в частности, сужение
и, в частности, сужение 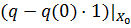 минорирует
минорирует 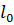 на
на 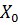 . По Теореме Хана - Банаха существует функционал
. По Теореме Хана - Банаха существует функционал 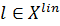 с сужением
с сужением 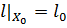 , мажорирующий
, мажорирующий 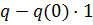 на
на  . Тогда аффинный функционал
. Тогда аффинный функционал 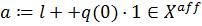 мажорирует
мажорирует 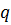 на
на  и удовлетворяет равенству
и удовлетворяет равенству  .
.
Пусть теперь зафиксировано 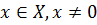 . Рассмотрим векторное подпространство
. Рассмотрим векторное подпространство 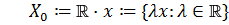 . Сужение
. Сужение 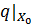 на
на 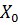 можно рассматривать в этом случае как вогнутую функцию
можно рассматривать в этом случае как вогнутую функцию 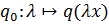 на
на  одной переменной с
одной переменной с 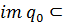
 . Тогда существует аффинная функция
. Тогда существует аффинная функция
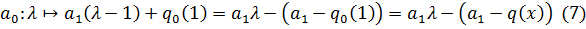
на  , где число
, где число 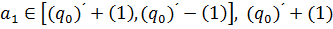 и
и 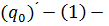 соответственно правая и левая производные функции
соответственно правая и левая производные функции  в точке
в точке 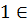
 и
и  в силу вогнутости функции
в силу вогнутости функции 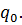 По построению функция
По построению функция 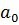 мажорирует функцию
мажорирует функцию  на
на  и
и 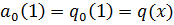 . Положим
. Положим
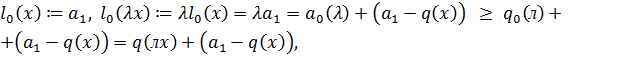

 .
. 
Эти соотношения определяют линейный функционал 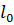 на
на 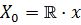 , который мажорирует вогнутый функционал
, который мажорирует вогнутый функционал
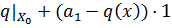
на 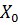 и при этом
и при этом
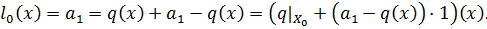
Отсюда по Теореме Хана-Банаха существует функционал 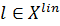 с сужением
с сужением 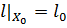 , мажорирующий вогнутый функционал
, мажорирующий вогнутый функционал
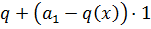
на  . Тогда аффинный функционал
. Тогда аффинный функционал
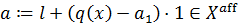
мажорирует 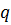 на
на  и удовлетворяет равенству
и удовлетворяет равенству
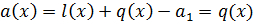 ,
,
что и требовалось.
Заключение.
В настоящей ВКР мы рассмотрели различные варианты теоремы Хана – Банаха. Были приведены классическая версия теоремы, теорема Хана-Банаха для комплексного случая, теорема Хана – Банаха для нормированных пространств и следствия из нее (теоремы о разделении выпуклых множеств).
Основную ценность представляет раздел, в котором нами получен полный аналог классической Теоремы Хана – Банаха для вогнутых функционалов, в котором роль линейных функционалов играют аффинные.
Представляет интерес распространение полученных в данной работе результатов на другие классы функционалов, в которых мы отказываемся в части требований, касающихся сублинейности. Например, от однородности или субаддитивности. Также интересно рассмотреть версии теоремы Хана – Банаха для алгебраических структур: групп, полугрупп, колец и т.д. Но это тема для дальнейших отдельных исследований.
Список использованной литературы.
[1]. Хабибуллин Б.Н. Двойственное представление суперлинейных функционалов и его применения в теории функций. Известия РАН, Серия матем. 2001. Т. 65, №4. С. 205-224
[2]. Кутателадзе С.С., Рубинов А.М. Двойственность Минковского и ее приложения. – Новосибирск: Наука, 1976.
[3]. Кусраев А.Г., Кутателадзе С.С. Субдифференциальное исчесление. Теория и приложения. – М.: Наука, 2007.
[4]. Мейер П.-А. Вероятность и потенциалы. – М.: Мир, 1973.
[5]. Акилов Г.П., Кутателадзе С.С. Упорядоченные векторные пространства. – Новосибирск: Наука, 1978.
Date: 2015-07-02; view: 471; Нарушение авторских прав