Теорема Хана-Банаха о продолжении линейных функционалов в вещественных линейных пространствах

Задача о продолжении линейного функционала часто встречается в анализе. Основную роль в этом круге вопросов играет следующая теорема:

Теорема (Хан - Банах). Пусть вещественное линейное пространство и 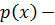вещественная функция, заданная на и удовлетворяющая следующим условиям:

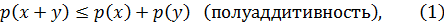
Пусть 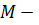вещественное линейное подпространство в 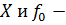вещественный линейный функционал, заданный на :

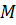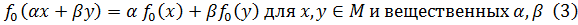
Пусть удовлетворяет неравенству 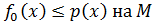. Тогда существует вещественный линейный функционал 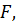определенный на 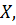такой, что 1) 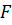служит продолжением 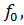т.е. 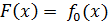для всех 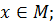2) .

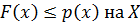Доказательство. Предположим сначала, что пространство натянуто на 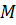и некоторый элемент 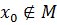, т.е.

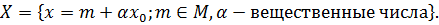
Так как 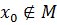, представление элементов 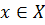в виде 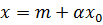определяются однозначно. Следовательно, полагая

где 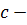произвольное вещественное число, мы получим вещественный линейный функционал 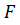на , являющийся продолжением . Мы должны теперь выбрать 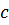таким, что 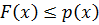, т.е. 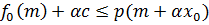. Последнее неравенство эквивалентно следующим условиям:

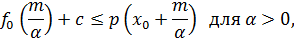
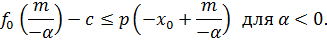
Чтобы выполнялись эти условия, мы выберем 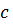так, что

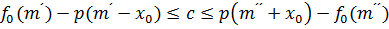
для всех 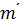, 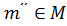. Такой выбор возможен, поскольку

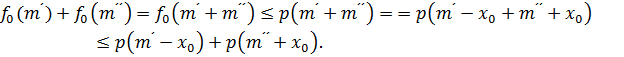
Итак, остается лишь выбрать 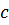между двумя числами

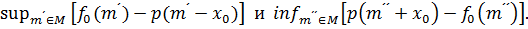
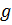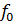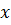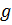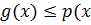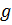Рассмотрим теперь семейство всех вещественных линейных продолжений функционала , для которых при всех на области определения выполняется неравенство ). Мы можем частично упорядочить это семейство, полагая функционал продолжением . Тогда по лемме Цорна существует максимальное линейное продолжение 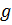функционала 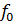, для которого неравенство 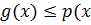) выполняется при всех 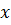из области определения 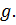Остается показать, что область определения 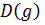функционала 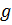совпадает с пространством . 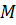Если бы это было не так, мы могли бы, приняв за подпространство , а сам функционал 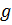за 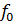, построить продолжение 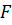функционала 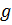, удовлетворяющее неравенству 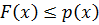для всех 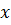из области определения 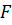. Но это противоречит максимальности линейного продолжения .

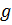Следствие из теоремы 2.1. Если на вещественном линейном пространстве задана функция , удовлетворяющая условиям (1) и (2), то существует определенный на линейный функционал 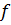, такой, что

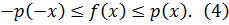
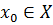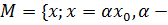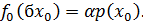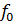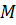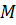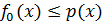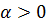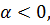Доказательство. Возьмем произвольную точку и определим множество любые вещественные числа}. Положим Тогда представляет собой вещественный линейный функционал с областью определения . На множестве неравенство выполняется. В самом деле, если , то а если то 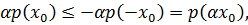поскольку 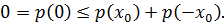Значит, существует линейный функционал 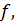определенный на линейном пространстве 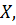такой, что 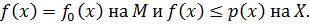Поскольку 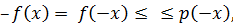мы получаем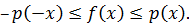

2.2.Комплексный вариант теоремы Хана – Банаха

Неотрицательный функционал 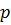на комплексном линейном пространстве 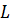называется однородно-выпуклым, если для всех 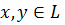и всех комплексных чисел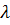

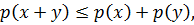
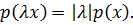
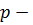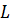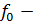Теорема 3.1. Пусть однородно-выпуклый функционал на комплексном линейном пространстве , а линейный функционал, определенный на некотором линейном подпространстве 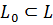и удовлетворяющий на нем условию

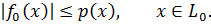
Тогда существует линейный функционал 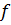, определенный на всем 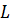и удовлетворяющий условиям

Доказательство. Обозначим через 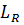и 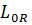пространство 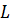и 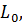рассматриваемые как действительные линейные пространства. Ясно, что 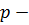однородно-выпуклый функционал н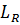а , а 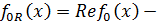действительный линейный функционал на 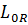, удовлетворяющий условию

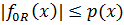
и, тем более, условию

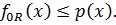
В силу Теоремы Хана-Банаха о продолжении линейных функционалов в вещественных линейных пространствах, существует действительный линейный функционал 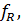определенный на всем 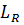и удовлетворяющий условиям

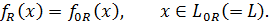
Ясно, что

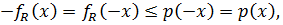
так что

Date: 2015-07-02; view: 1034; Нарушение авторских прав