Сущность метода

Энергетические теоремы и их применение в приближенных расчетах

Метод, называемый энергетическим, связан с законом сохранения энергии и теоремой Лагранжа-Дирихле о минимуме потенциальной энергии. Для системы с распределенными параметрами удобны следующие формулировки:

- Консервативная система находится в равновесии, когда полная потенциальная энергия системы стационарна (производная по изменяемому параметру равна нулю);

- Положение равновесия консервативной системы устойчиво тогда и только тогда, когда стационарное значение потенциальной энергии - изолированный минимум.

Метод позволяет приближенно решать задачи определения параметров НДС, в том числе и в критических состояниях. Степень приближенности соответствует степени адекватности математической модели.

Введем обозначения:

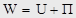, (1)

где W - полная потенциальная энергия системы,

U – потенциальная энергия упругой деформации (всегда положительна, та как усилие на упругом элементе всегда направлена против перемещения,

П – потенциал внешних сил (отрицательный при совпадении направлений силы и перемещения).

Проиллюстрируем метод на простом примере.

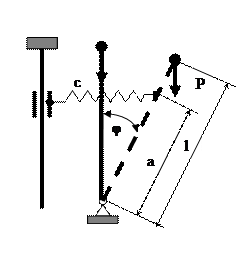
В вертикальном положении пружина не деформирована. Стержень абсолютно жесткий. В отклоненном состоянии , ,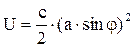

.

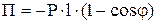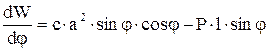Условие равновесия 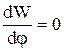дает два решения: не отклоненное 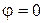и отклоненное .

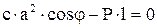
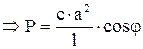Условие их устойчивости .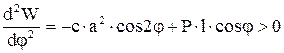

В не отклоненном состоянии равновесие устойчиво при 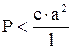, в отклоненном, подставляя значение Р, получаем и равновесие неустойчиво.

Вывод справедлив только для абсолютно жесткого стержня. Для гибкого стержня необходимо учесть потенциальную энергию 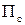его деформации (изгиба и сжатия). Решение задачи будет иным. Аналитическое решение возможно только в тех случаях, когда удается записать функцию W в квадратурах и решить уравнения равновесия и проанализировать знак второй производной без применения численных методов. Во всех других случаях решение можно получить численно.

Рассмотрим потенциальную энергию упругого тела.

Date: 2015-07-02; view: 308; Нарушение авторских прав