
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Моменты инерции простейших сечений
|
|
Осевые моменты инерции прямоугольника (рис. 25.2)
Представим прямоугольник высотой h и шириной b в виде сечения, составленного из бесконечно тонких полос. Запишем площадь такой полосы: bdy=dA. Подставим в формулу осевого момента инерции относительно оси Ох:
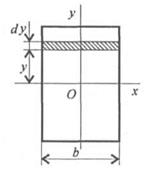 Рис.
Рис.
| 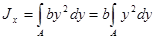 ; ;
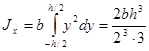 ; получим: ; получим: 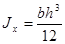 .
По аналогии, если разбить прямоугольник на вертикальные полосы, рассчитать площади полос и подставить в формулу для осевого момента инерции относительно оси Оу, получим: .
По аналогии, если разбить прямоугольник на вертикальные полосы, рассчитать площади полос и подставить в формулу для осевого момента инерции относительно оси Оу, получим:
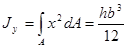 . .
|
Очевидно, что при h > b сопротивление повороту относительно оси Ох больше, чем относительно Оу.
Для квадрата: h = b; 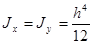 .
.
| Полярный момент инерции круга Для круга вначале вычисляют полярный момент инерции, затем - осевые. Представим круг в виде совокупности бесконечно тонких колец (рис. 25.3). Площадь каждого кольца можно рассчитать как площадь прямоугольника с длинной стороной, равной длине соответствующей окружности, и высотой, равной толщине кольца: dA = 2πpdp. Подставим это выражение для площади в формулу для полярного момента инерции: | 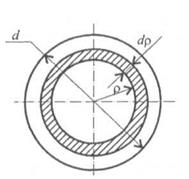 Рис.
Рис.
|
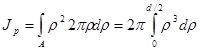 ;
; 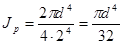 .
.
Получим формулу для расчета полярного момента инерции круга:
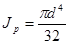 .
.
Подобным же образом можно получить формулу для расчета полярного момента инерции кольца:
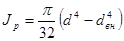 ,
,
где d - наружный диаметр кольца; dBH - внутренний диаметр кольца.
Если обозначить dBH / d = с, то
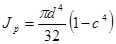 .
.


 Осевые моменты инерции круга и кольца
Осевые моменты инерции круга и кольца
Используя известную связь между осевыми и полярным моментами инерции, получим:
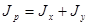 ;
; 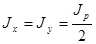 ;
;
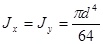 (круг);
(круг); 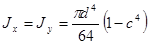 (кольцо).
(кольцо).
Date: 2015-07-02; view: 1644; Нарушение авторских прав