
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Формулы Эйлера
|
|
Показательная формула записи. Леонардо Эйлер распространил понятие степени на случай комплексного показателя. Он предложил (не получил!, не доказал!) считать, что
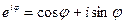 (6)
(6)
в случае, если 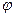 какое-либо действительное число. Формула (6) носит название формулы Эйлера. Здесь показатель степени чисто мнимый.
какое-либо действительное число. Формула (6) носит название формулы Эйлера. Здесь показатель степени чисто мнимый.
В случае любого комплексного числа 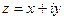 по аналогии будем иметь
по аналогии будем иметь
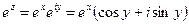 (7).
(7).
Эта формула тоже не доказывается, а является отображением действия 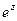 .
.
Такое определение позволяет распространить на случай комплексных показателей все остальные свойства показателей степени и, таким образом, подключить к операциям с комплексными числами уже созданный математический аппарат.
Действительно, если 
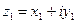 и
и 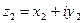 , то
, то
1. 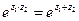 , 2.
, 2. 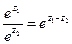 , 3.
, 3. 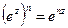 (
(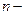 натуральное число).
натуральное число).
Доказательство свойств 1., 2., 3., рекомендуем читателям выполнить в качестве упражнения.
Из (6) и тригонометрической формы записи комплексного числа легко прийти к показательной форме его записи 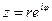 (8).
(8).
Здесь 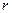 - модуль числа
- модуль числа 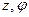 - аргумент.
- аргумент.
В такой записи формула Муавра принимает вид  , а формулы для нахождения корня
, а формулы для нахождения корня 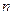 -ой степени-
-ой степени- 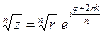 ,
, 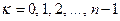 .
.
Если в (6) заменить 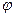 на
на 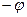 , то получим
, то получим 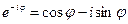 (7)
(7)
Из (6) и(7) получаем очень полезные и часто употребляемые формулы
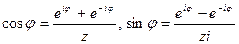 (8), которые также называют формулами Эйлера. Обращаем внимание, что с помощью этих формул тригонометрические функции от вещественного аргумента выражаются через показательные функции от чисто мнимых аргументов.
(8), которые также называют формулами Эйлера. Обращаем внимание, что с помощью этих формул тригонометрические функции от вещественного аргумента выражаются через показательные функции от чисто мнимых аргументов.
Задачи
1. Показать, что если 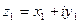 и
и 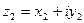 , то
, то 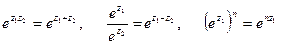
Тест
1. Число, записанное в координатной, тригонометрической и показательной форме
а) имеет один и тот же модуль, б) имеет разные аргументы, в) имеет один и тот же модуль, но разные аргументы
2. Справедливо ли утверждение 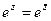
а) справедливо, так как cosφ- чётная функция,
б) несправедливо, так как sinφ – нечётная функция,
в) справедливо, так как cosφ – чётная функция, а sinφ – нечётная.
 8. [1] Функции комплексного переменного и примеры их практического применения
8. [1] Функции комплексного переменного и примеры их практического применения
Говорят, что на каком-то множестве М точек плоскости задана функция 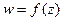 , если указан закон, по которому каждой точке z из М ставится в соответствие определенная точка или совокупность точек
, если указан закон, по которому каждой точке z из М ставится в соответствие определенная точка или совокупность точек 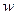 . В первом случае функция
. В первом случае функция 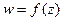 называется однозначной, во втором – многозначной. Множество М называется множеством определения функции
называется однозначной, во втором – многозначной. Множество М называется множеством определения функции  , а совокупность N всех значений
, а совокупность N всех значений 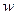 , которые
, которые  принимает на М – множеством её изменения. Наиболее важную роль в приложениях играет случай, когда М и N являются областями, то есть обладают свойствами открытости и связности. Открытость – вместе с каждой точкой из множества этому множеству и достаточно малый круг с центром в этой точке. Связность – любые две точки множества можно соединить ломаной, состоящей из точек этого множества.
принимает на М – множеством её изменения. Наиболее важную роль в приложениях играет случай, когда М и N являются областями, то есть обладают свойствами открытости и связности. Открытость – вместе с каждой точкой из множества этому множеству и достаточно малый круг с центром в этой точке. Связность – любые две точки множества можно соединить ломаной, состоящей из точек этого множества.
Если положить 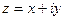 и
и 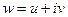 , то задание функции комплексного переменного
, то задание функции комплексного переменного 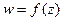 будет равносильным заданию двух функций двух действительных переменных:
будет равносильным заданию двух функций двух действительных переменных: 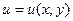 и
и 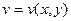 .
.
Даже такие простейшие понятия из теории функций комплексного переменного позволяют получить результаты не менее удивительные, чем рассмотренные в §4 и §6. Вот пример из работ Н.Е. Жуковского и С.А. Чаплыгина, лежащий в основе теории профиля крыла (самолета, корабля и т.д.). За основу физической модели обтекающего потока были приняты уравнения движения плоскопараллельного течения идеальной несжимаемой жидкости. В этом случае оказывается, что воздействие потока на единицу размаха крыла приводит к математическому исследованию некоторых классов функций комплексного переменного. Если рассмотреть функцию 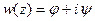 , то как предположил Н.Е. Жуковский, функция
, то как предположил Н.Е. Жуковский, функция 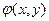 будет соответствовать потенциалу скоростей (вспомните основы теории поля!) плоскопараллельного течения идеальной несжимаемой жидкости, а функция
будет соответствовать потенциалу скоростей (вспомните основы теории поля!) плоскопараллельного течения идеальной несжимаемой жидкости, а функция 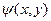 - функции тока этого течения. Условие
- функции тока этого течения. Условие 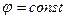 будет определять семейство линий с одинаковым потенциалом, а
будет определять семейство линий с одинаковым потенциалом, а 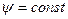 - семейство линий тока.
- семейство линий тока.
Компоненты вектора скорости  (по оси ох) и
(по оси ох) и 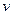 (по оси оу) какой либо частицы воздуха (жидкости или газа) определяются следующими соотношениями:
(по оси оу) какой либо частицы воздуха (жидкости или газа) определяются следующими соотношениями:
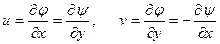 . Условия Д'Аламбера-Эйлера; (
. Условия Д'Аламбера-Эйлера; (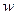 - так называемая, аналитическая функция).
- так называемая, аналитическая функция).
Из 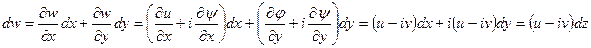 следует, что
следует, что 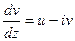 .
.
Таким образом установлено, что производная от комплексного потенциала позволяет найти действительные (вещественные) компоненты вектора скорости.
Литература
1. Г. М. Фихтенгольц, Курс дифференциального и интегрального исчисления, т.2, ФМ, М., 1959г.
2. Г. П. Толстов, Элементы математического анализа, т. 1, ФМ, М., 1974г.
3. Ф. И. Маркушевич, Комплексные числа и комформные отображения, 2-ое изд., М., 1960г.
Словарь основных терминов
мнимая единица: 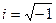 , то есть число, квадрат которого равен -1 (i2 = -1).
, то есть число, квадрат которого равен -1 (i2 = -1).
число z = x + iy называется комплексным (иногда «мнимым») числом, если x и y какие- либо действительные числа.
действительной или вещественной частью комплексного числа z называют число x, а число y - его мнимой частью. Часто употребляется обозначение x = Re z, y=Im z (от слов re ality и im aginaire, фр.)
модулем или абсолютной величиной комплексного числа z называется неотрицательное число r, вычисляемое по формуле 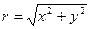 .
.
аргументом, реже фазой комплексного числа называют угол φ (см. полярные координаты и рис. 1)и пишут φ = Arg z. При z ≠ 0 аргумент определяется по формулам cos j = 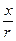 , sin j =
, sin j = 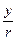
Сложение комплексных чисел определяется следующим образом
z1 +z2 = (х1 + iy1) + (x2 + iy2) = (x1 + x2) + i(y1 + y2)
Вычитание комплексных чисел вводится как разность z1 и z2, то есть z1 – z2 = (x1 + iy1) – (x2 + iy2) = (x1 – x2) + i(y1 – y2).
Корнем 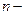 ой степени из комплексного числа
ой степени из комплексного числа 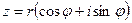 называется такое комплексное число
называется такое комплексное число 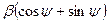 , что
, что 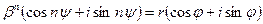 . Где
. Где 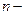 натуральное число.
натуральное число.
Умножение двух комплексных чисел проводится по правилам умножения многочленов с учётом правила возведения в степень мнимой единицы I:
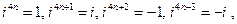 где n- любое натуральное число.
где n- любое натуральное число.
При 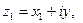 и
и 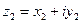 :
:

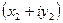 =
= 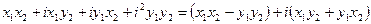 .
.
Date: 2015-07-02; view: 1285; Нарушение авторских прав