Комплексные числа в полярных координатах

Применим полярные координаты (r,φ) на комплексной плоскости z (рис.1). Неотрицательное число r называется модулем или абсолютной величиной комплексного числа z. Из рис.1 видно, что применяя формулы теоремы чемпиона Олимпийских игр по кулачному бою, Пифагора с острова Самос, легко получить .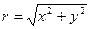

Ясно, что r по модулю всегда больше или равен нулю, причём r = 0 лишь в том случае, когда z = 0. Отметим, что для модулей двух комплексных чисел z₁ и z₂ естественным образом выполняется неравенство Минковского. Действительно, если z₁ = х₁ + iу₁ и z₂ = x₂ +iy₂, то 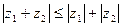или

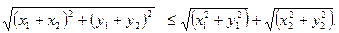Это становится очевидно, если вспомнить про геометрический смысл |z₁|, |z₂| и |z₁ + z₂|.

Угол φ обычно называют аргументом, реже фазой комплексного числа и пишут φ = Arg z. При z ≠ 0 аргумент определяется по формулам (см. рис.1)

cos j = 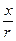, sin j = 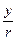, (1)

но согласно правилам тригонометрии, с точностью до 2πк (к− целое) то есть является действительной многозначной функцией. Обычно используется главное значение аргумента arg z, удовлетворяющее неравенствам –π< φ ≤π в этом случае у каждого числа z существует лишь один аргумент.

В случае z = 0 аргумент не определён и может считаться любым. Если вспомнить из школьного курса тригонометрии формулу для тангенса половинного угла, то используя (1), можно записать

tg 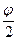= = 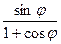= 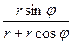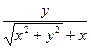, j > p.

Стало быть, для главного значения аргумента

arctg z = 2 arc tg ,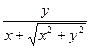

что является верным для всех комплексных чисел, кроме действительных, отрицательных и нуля.

Применение полярных координат позволяет получить тригонометрическую (иногда её называют «полярной») форму комплексного числа. Для этого нужно вместо х и у в определение комплексного числа подставить их выражения из (1). Получим

z = r(cos φ + i sin φ).

Любое действительное число А может быть представлено в виде комплексного (тригонометрическая форма) следующим образом.

A = 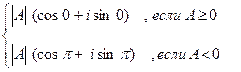(2)

Пример:

2 = 2(cos 0 + i sin 0) или

-17 = 17(cos π + i sin π).

Пример: Запишем число z = (-8) в тригонометрической форме: , .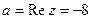

.

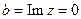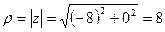
Т.к. z находится в левой полуплоскости, то 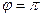. Тригонометрическая форма этого числа имеет вид: .

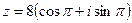Пример: Запишем число 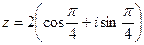в алгебраической форме. Модуль z = 2, а аргумент .

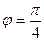Его действительная часть 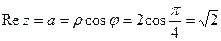, а мнимая часть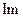 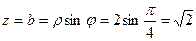. Таким образом, алгебраическая форма числа z имеет вид .

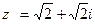Пример:

1) Вычислить модуль числа 3+4i

Re (3+4i)=3; Im(3+4i)=4; r =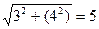

2) Найти главное значение аргумента числа 3-4i

argz = 2 arctg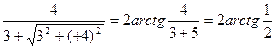

3) Записать комплексное число 1 в тригонометрической форме.

1 = 1(cos0 + isin0)

Задачи

1. Записать в тригонометрической форме числа 3+4i, -1+2i, - ,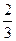

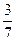
2. Найдите модуль комплексных чисел 3i, 3, 1, i.

3. Запишите числа 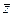и 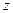в тригонометрической форме

Тест

1. Что такое φ?

а) одна из фаз трёхфазного электродвигателя,

б) Фаза или аргумент комплексного числа,

в) угол между радиус-векторам комплексного числа и осью OY.

2. У чисел имеет 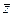и

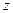
а) аргументы будут равными,

б) модули будут равными,

в) модули будут равными, а аргументы нулевыми,

г) и аргументы и модули будут равными

3. У комплексного числа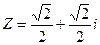

а) ReZ = ImZ,

б) r=1,

в) φ= .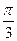

Date: 2015-07-02; view: 1730; Нарушение авторских прав