Пункт 1. Понятие комплексного числа. Тема 6.1. Алгебраическая форма записи комплексного числа

РАЗДЕЛ 6. ОСНОВЫ ТЕОРИИ КОМПЛЕКСНЫХ ЧИСЕЛ

Тема 6.1. Алгебраическая форма записи комплексного числа.

План:

Понятие комплексного числа.

Геометрическая интерпретация комплексного числа.

Арифметические действия над комплексными числами.

Пункт 1. Понятие комплексного числа.

Опр1. Символ a + bi называют комплексным числом с действительной частью a и мнимой частью bi, где a и b – действительные числа, b – коэффициент мнимой части.

Опр2. Во множестве комплексных чисел существует элемент i (мнимая единица) такой, что i² = – 1.

Комплексное число a + 0i отождествляется с действительным числом a, т.е. a + 0i = a, в частности, 0 + 0i = 0. Числа вида bi (b ≠ 0) называют чисто мнимыми.

Например, комплексное число 2 + 3i имеет действительную часть – действительное число 2 и мнимую часть 3i, действительное число 3 – коэффициент мнимой части.

Комплексное число 2 – 3i имеет действительную часть число 2, мнимую часть – 3i, число – 3 – коэффициент при мнимой части.

Опр3. Для любого комплексного числа существует комплексное число, противоположное данному. Оно обозначается - z = -a - bi.

Опр4. Для любого комплексного числа существует сопряженное комплексное число, которое отличается от данного противоположным знаком перед мнимой частью. Такое число обозначается 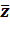= a – bi.

Свойства сопряженных комплексных чисел:

· (сопряжённое к сопряжённому есть исходное).

·

·

·

·

·

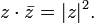
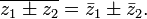
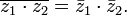
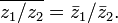
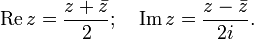
Опр5. Запись комплексного числа z = a + bi называется алгебраической формой записи комплексного числа.

Перейдем теперь к вопросу о решении полного квадратного уравнения. Квадратным уравнением называют уравнение вида: ax² + bx + c = 0, где x – неизвестная, a, b, c – действительные числа, соответственно первый, второй коэффициенты и свободный член, причем a ≠ 0. Решим это уравнение, выполнив над ним ряд несложных преобразований.

Разделим все члены уравнения на a ≠ 0 и перенесем свободный член в правую часть уравнения: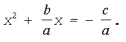

К обеим частям уравнения прибавим выражение с тем, чтобы левая его часть представляла полный квадрат суммы двух слагаемых:

Извлечем корень квадратный из обеих частей уравнения: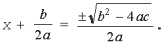

Найдем значения неизвестной: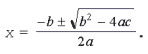

Теперь можно исследовать полученное решение. Оно зависит от значения подкоренного выражения, называемого дискриминантом квадратного уравнения. Если b2 – 4ac > 0, то 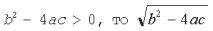есть действительное число и квадратное уравнение имеет действительные корни. Если же – мнимое число, квадратное уравнение имеет мнимые корни.

Результаты исследования представлены ниже в таблице:

Итак, введение комплексных чисел позволяет разработать полную теорию квадратных уравнений. В поле комплексных чисел разрешимо любое квадратное уравнение.