Набор дискриминаторов

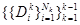
Заданный набор отношений 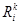определяет набор классов эквивалентности:

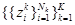
Дискриминатор 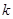-го уровня выбирает одного представителя 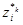из множества вариантов

алгоритмов 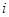-гo класса эквивалентности. Пусть на некотором 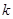-м уровне имеются 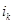классов эквивалентности, смежных одному классу эквивалентности более высокого уровня 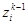. Классы эквивалентности 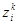уровня 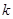имеют следующие множества представителей:

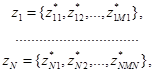
где 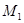- число представителей в 1-м классе эквивалентности 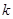-гo уровня.

Тогда процесс построения представителей некоторого 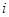-го класса эквивалентности 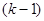-го уровня задается следующей процедурой:

1) выбирается один из возможных представителей каждого класса эквивалентности 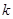-го уровня;

2) выполняется над представителями заданная операция 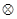или .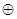

Рассмотрим выполнение этой процедуры на примере. Пусть имеется некоторый фрагмент дерева действий, адекватного декомпозиции целевой задачи предметной области (рис.3.3). Для каждого уровня этого дерева запишем формулу эксперимента:

; ;

; ;

; ;

; ;

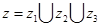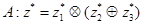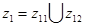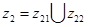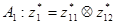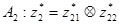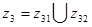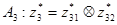Пусть исходный алфавит имеет следующий набор символов:

.

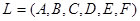Пусть классы эквивалентности нижнего уровня вэтом примере имеют следующие наборы представителей:

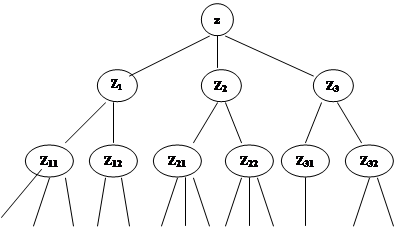
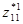
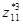
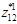
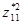
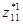
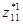
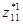
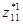
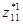
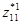
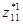
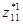
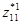
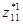
Рис.З.З.Фрагмент дерева действия

;

;

;

;

;

.

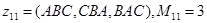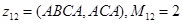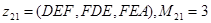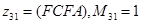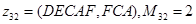где 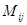- число представителей.

Пусть в результате селекции представителей для организацииалгоритма на нижнем уровне выбраны последние цепочки. Тогда в соответствии с формулами построения алгоритмов болеевысокого уровня совокупная цепочка имеет вид

.

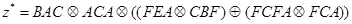Определим количество представителей в классах эквивалентности накаждом уровне:

;

;

;

.

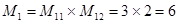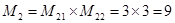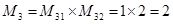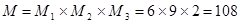В рассматриваемом примере получено, что один из вариантов алгоритма эксперимента верхнего уровня реализуется с помощью цепочки действия 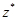, а всего существует 108 различных вариантов экспериментов.

Определим общее число вариантов построения алгоритмов экспериментов в многоуровневой системе управления экспериментами.

Поскольку число вариантов выбора представителей из каждого класса на 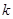- м уровне равно числу членов этого класса, количество представителей, в классе эквивалентности 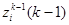- го уровня определится как произведение числа представителей каждого класса 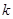- го уровня, смежного с классом :

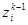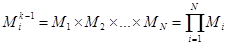. (3.17)

Двигаясь по дереву функциональной организации алгоритмов проведения комплексных экспериментов "снизу вверх", получаем, что на нижнем уровне иерархии для каждого класса эквивалентности 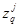число вариантов выбора элементов алгоритма эксперимента равно количеству представителей в данном классе эквивалентности. Для каждого класса 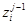более высокого уровня 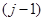число альтернатив выбора вариантов построения алгоритма существенно больше и определяется произведением числа вариантов выбора в классах уровня 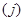, смежных с классом 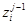в соответствии с выражением (3.17).

Общее число альтернатив выбора варианта организация алгоритма эксперимента в многоуровневой автоматизированной системе определяется произведением числа альтернатив выбора вариантов по всем классам эквивалентных действий нижнего уровня иерархии:

,

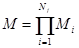где 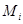- число альтернатив выбора вариантов в 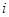- м классе эквивалентности нижнего уровня; 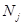- число классов эквивалентности нижнего уровня. Для оценки числа альтернатив выбора вариантов организации алгоритмов на верхнем уровне иерархии предположим, что в каждом классе эквивалентности нижнего уровня имеется одинаковое число представителей, равное 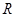, а число таких классов равно 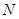. 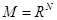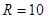Тогда общее число вариантов выбора алгоритма эксперимента для многоуровневой системы будет равно для и 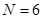получаем 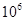различных реализации вычислительного процесса. Таким образом, алгоритм эксперимента в сложной многоуровневой автоматизированной системе можно реализовать довольно большим числом вариантов.

Отождествим варианты выполнения эквивалентных действий (представителей внутри одного класса эквивалентности) с вершинами некоторого графа 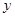, а отношения выбора представителей 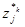- с ребрами этого графа. Поскольку выбор альтернатив проводится внутри классов эквивалентности дерева действий, то построенный граф 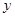тоже будет деревом. Назовем граф 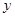деревом альтернатив выбора вариантов организации алгоритмов проведения экспериментальных научных исследований. Корнем этого дерева является выбор представителя внутри класса эквивалентных действий на самом нижнем уровне иерархии (выбор внутри листа дерева действий), а листьями - варианты организации всего рассматриваемого алгоритма в целом. Таким образом, чем ближе к корню дерева осуществляется выбор варианта алгоритма эксперимента, тем большее число альтернатив нужно рассмотреть.

Для сравнения вариантов организации алгоритмов управления необходимо задать параметры, характеризующие эти алгоритмы. Одним из таких параметров, имеющих практическое значение, может быть время выполнения вычислительного эксперимента. В качестве другого параметра могут использоваться, например, затраты памяти или других ресурсов вычислительных средств [6], необходимые для реализации алгоритма управления данным экспериментом. Рассмотрим задачу определения параметров алгоритма управления сложным вычислительным экспериментом, состоящим из большого числа различных действий.

Для определения параметров алгоритма многоуровневогоуправления воспользуемся рекуррентной моделью. Поскольку в этом случае алгоритм представляется в виде совокупности цепочек элементарных (атомарных) действий, то остается определять параметры используемых атомов и установить правила построения совокупного параметра цепочки по известным параметрам атомов. Пусть каждый атом на нижнем уровне иерархии рекуррентной структуры управления характеризуется некоторыми параметрами 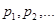и т.д. Поскольку используемая модель задает отображения между уровнями иерархии управления, то для задания способа вычисления некоторого совокупного параметра цепочки определим отображение алгебры цепочки на соответствующую алгебру параметров: 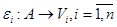, где 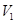- алгебра первых параметров;

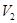- алгебра вторых параметров и т.д.; 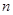- число параметров.

Поскольку всякий элемент цепочки характеризуется только одним значением каждого параметра и цепочка в целом - тоже одним значением соответствующего параметра, то все отображения 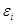должны быть гомоморфизмами;

,

,

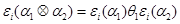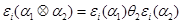где 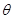- некоторая операция в алгебре соответствующего параметра 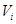. Вид операции 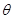определяется на основании физического смысла конкретных параметров. Например, если в качестве одного из параметров элементов цепочки выбрано время их реализаци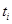и и 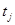, то время 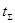, выполнения всей цепочки будет определяться для операции 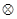суммированием времени выполнения элементов, а для операции 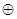- определением максимума:

,

.

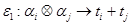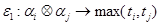Таким образом, на основе данных о параметрах атомов алгоритма управления можно построить параметры всего алгоритма в целом. Для выбора конкретного варианта из некоторого множества алгоритмов с известными параметрами необходимо задать критерии качества выполняемых действий по управлению и правило, во которому будет выбираться тот или иной вариант в зависимости от значения критерия. Выбор оптимального в смысле введенного критерия варианта организации алгоритма сводится к известным задачам дискретной оптимизации, которые могут решаться известными методами направленного перебора. Число альтернатив выбора минимально на нижнем уровне декомпозиции и максимально на верхнем. Поэтому аппарат дискретной оптимизации эффективно использовать в сочетании с эвристическими приемами исследователей при выборе квазиоптимальных алгоритмов на основе неформальных знания о преимуществах конкретных путей декомпозиции задачи организации управления. Системные затраты на оптимизацию будут тем меньше, чем ближе к нижнему уровню будет включаться аппарат дискретной оптимизации. На нижнем уровне декомпозиции оптимизируется структура примитивов, в которой число вариантов выбора ограничено десятками и возможен простой перебор. Такой аппарат эвристической оптимизации реализует рассматриваемая ниже система LEADER.

Пусть выполнение каждого примитива осуществляется одной или несколькими цепочками атомов. Набор всевозможных атомов, имеющихся в распоряжении представителей исследовательского коллектива, образует функциональный алфавит: 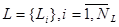. Таким образом, примитивы также оказываются классами эквивалентности, элементами которых являются цепочки атомов. Следовательно, для полного определения алгоритма эксперимента в системе мало определить необходимые для его проведения примитивы, необходимо также выбрать конкретные цепочки атомов, реализующих тот или иной примитив. Продолжение декомпозиции по признаку функциональной направленности ниже уровня примитивов невозможно, поскольку все цепочки атомов, относящиеся к данному примитиву, функционально эквивалентны. Необходимо, следовательно, выбрать из цепочек атомов такую, которая обеспечивает выполнение примитивной функции наилучшим образом (быстрее, с наименьшими затратами ресурсов в т.п.). Данная задача будет решена, если определять критерий качества

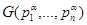
где 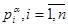, - параметры цепочки 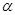, и реализовать соответствующий алгоритм оптимизации этого критерия. Оптимальная цепочка доставляет максимум критерию качества:

.

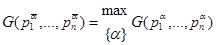Для определения параметров цепочки 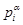необходимо знать, во-первых, соответствующие параметры отдельных атомов 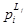(что для практических систем достижимо) и, во-вторых, отображения 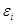алгебры цепочек 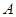на алгебры соответствующих параметров 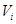. Примеры построения отображений рассмотрены выше.

Выбор на может рассматриваться как оптимизационная задача на множестве строк символов и решаться простым перебором либо при значительной мощности одним из методов направленного перебора.

Date: 2015-07-02; view: 636; Нарушение авторских прав